A spinner consist of 8 equal regions as shown. What is the probability in percent form that the arrow will land in region A and then spun again land on D?

Step-by-step explanation:

At first let's understanding the question,

In this following questions it has given that;

Difference of two numbers is 19. If the smaller number is 18, we have to find the greater

number.

According to the question:-

let the Greater no is =G

in question, The smaller no is =18

The difference of two no is =19

Solution:-

From the question,

Final answer:-

\(\therefore\) The greater no is 37.

Given:

A circle with a center at C.

Required:

We need to find the names of the given parts.

Explanation:

Recall that radius is a line segment extending from the center of a circle to the circumference.

Line segment AC extends from the center C of a circle to the circumference.

Recall that the arc of a circle is defined as the part of the circumference of a circle.

AE is the part of the circumference of a circle.

Recall that a straight line segment joins and is included between two points on a circle.

D and E are two points on a circle.

A straight line DE line segment joins and is included between two points D and E on a circle.

Recall that meeting a curve or surface in a single point if a sufficiently small interval is considered a straight line tangent to a curve.

AB is tangent.

Recall that an inscribed angle is an angle with its vertex "on" the circle, formed by two intersecting chords.

Recall that a central angle is an angle formed by two radii with the vertex at the center of the circle.

Recall that an angle formed by an intersecting tangent and chord has its vertex "on" the circle.

Final answer:

Answer:

66-26 = 40

Step-by-step explanation:

u = 40 degrees

Answer:

This answer would be c

Step-by-step explanation:

The midpoint is 26.

Midpoint in this scenario = mean

(23+29)/2 = 26

Answer:

-6

Step-by-step explanation:

Given:

Two electrons are added to each of six atoms in a group.

To find:

The expression for the net change in charge.

Solution:

Charge of atoms = Number protons - Number of electrons.

Let number of atoms be x.

6 atoms = 2 electrons added

1 atom = \(\dfrac{2}{6}\) electrons added

1 atom = \(\dfrac{1}{3}\) electrons added

x atoms = \(\dfrac{1}{3}x\) electrons added

Therefore, the net change in charge is represented by the expression \(-\dfrac{1}{3}x\) because we subtract number of electrons to find atom charge, where, x is the number of atoms.

6 atoms = 2 protons removed

1 atom = \(\dfrac{2}{6}\) protons removed

1 atom = \(\dfrac{1}{3}\) protons removed

x atoms = \(\dfrac{1}{3}x\) protons removed

Therefore, the net change in charge is represented by the expression \(-\dfrac{1}{3}x\), where, x is the number of atoms.

Answer:

Adding two electrons to each of six atoms results in a net change in charge of (-2)(6). Removing two protons from each of six atoms results in a net change in charge of (2)(-6).

Step-by-step explanation:

I know this is right because i just did the problem and got it wrong then it showed the correct answer and that is the exact answer so you might wanna switch the answer up a little so you dont get in trouble

Answer:3.8

Step-by-step explanation:

Answer:

-13.64 millimeters

Step-by-step explanation:

just use a calculator ._.

Answer:

Step-by-step explanation:

43min=3miles

93min=3*93=279/43

austin will walk 6.488miles for 93 minutes

Answer:

31 vacuums

Step-by-step explanation:

1800 = 250 + 50v

1800 - 250 = 50v

50v = 1550

v = 1550 / 50

v = 31

He sold 31 vacuums.

We're given:

Let x equal the calorie count per serving of the original popcorn.

The light popcorn has a calorie count of 120, which is 25% fewer calories than regular popcorn. This means that 75% of the calorie count of regular popcorn is equal to that of the light popcorn:

\(x*0.75=120\)

\(x*0.75=120\)

⇒ Divide both sides by 0.75:

\(\dfrac{x*0.75}{0.75}=\dfrac{120}{0.75}\\\\x=160\)

Therefore, each serving of regular popcorn has 160 calories.

Answer:

Step-by-step explanation:

Question: Determine the equation of the parabola that opens up, has vertex (7,7), and a focal diameter of 16 . This problem has been solved! You'll get a detailed solution from a subject matter expert that helps you learn core concepts.

Answer: ((x2)−14x+87)/16

Step-by-step explanation:

  focal diameter = 16,

  4a=16;

  a=4.

(h,v)=(7,7-a)

==> (h,v)=(7,3)

the equation of the parabola =  ((x-7)^2)=16(y-3)

                                                => y = ((x^2)-14x+87)/16.

The volume of aggregate that she needs to build the patio is 13.18 ft^3

We know that the backyard is 14ft long, 6 feet wide and 4 inches deep.

Rememeber that:

1ft = 12 in

Then:

4 in = (4/12) ft = (1/3) ft

Then the volume of the backyard is:

V = (14ft)*(6ft)*(1/3 ft) = 28ft^3

Now we know that we have a mix of 4 parts aggregate to 4.5 parts loose cement that need to fill these 28 cubic feet.

Note that:

4 + 4.5 = 8.5

How many times we have 8.5 in 28?

28/8.5 = 3.294

Now for each of these we have 4 parts of aggregate, then the volume of aggregate that we need is:

4*3.294 ft^3 = 13.18 ft^3

The volume of aggregate that she needs to build the patio is 13.18 ft^3

If you want to learn more about volumes:

https://brainly.com/question/1972490

#SPJ1

Answer:

(13, -67.4°)

Step-by-step explanation:

In the general case, for a point (x, y), the same point written in polar coordinates is (r, θ), such that:

r = √(x^2 + y^2)

θ = Atg(y/x)

Then if we have the point with coordinates (-5, 12)

The polar coordinates will be:

r = √((-5)^2 + 12^2) = 13

θ = Atg(12/-5) = -67.4°

Then the polar coordinates are:

(13, -67.4°)

The probability that at least 2 of the colors will be the same, the following is the best simulation is Option D Put 5 pieces of paper in a bag, each labeled with a different color. For each trial, randomly select and replace a paper 7 times. Run 50 trials and find the fraction of times that at least two of the same color appear.

Given, Sienna buys a mystery pack of sparkly modeling clay. The pack has 5 colors, and there are 7 possible colors that are all equally likely. We have to find the probability that at least 2 of the colors will be the same. There are 5 colors in the pack of clay, and 7 colors are possible in total.

So, the probability of picking any color at random is

P(picking a color) = 5/7 = 0.7143Let P(X = 2) be the probability that exactly 2 of the colors are the same.

Then, the probability that at least 2 of the colors are the same can be calculated by using the formula:

P(X ≥ 2) = 1 - P(X < 2).

The simulation method that can be used to find the probability of at least 2 of the colors will be the same in the mystery pack is option D.

Put 5 pieces of paper in a bag, each labeled with a different color. For each trial, randomly select and replace a paper 7 times. Run 50 trials and find the fraction of times that at least two of the same color appear.

Know more about probability    here:

https://brainly.com/question/25839839

#SPJ8

Answer:

13.48

Step-by-step explanation:

So I used the Order of Operation and went in order to solve the problem. First is P (Parentheses)

(1.74) = 1.74

Next, Exponents (E).

There are none.

Then, Multiplication and Division (from left to right).

2(1.74) = 3.48 | 15-9+2.65+1.35+3.48.

The fourth is Addition and Subtraction (from left to right).

15-9+2.65+1.35+2= 13.48

Answer:

The roots of a quadratic equation simply tell what values of x will make the equation true. A quadratic function is a function where the largest power for the variable is 2. ... A quadratic equation is given to you so that you can solve it for the variable. A quadratic function is given to you so that you can graph it.

Answer: \(\frac{20}{3} %\)%

Step-by-step explanation:

Convert 3m to cm:

\((3m)(\frac{100cm}{1m} )=300cm\)

Now divide 20cm by 300cm:

20cm/300cm=1/15

Multiply (1/15) by 100% to convert the fraction to a decimal:

(1/15)(100%)=\(\frac{20}{3} %\)%

Answer:

Step-by-step explanation:

For step explanation:

1. write the problem

2. distinguishing the neg sign

3. distributing 3

4. moving like terms next to each other through commutative property

5.  Combining like terms

6. getting rid of parentheses

Answer:the law of sines is the relationship between the sides and angles of the ratio of the length of a side of triangle to the sine of the angle opposite that side is the same for all sides and angles in a given triangle

Step-by-step explanation:

Answer:

She should order 2400 coupons.

Step-by-step explanation:

Central Limit Theorem

The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).

For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean \(\mu = p\) and standard deviation \(s = \sqrt{\frac{p(1-p)}{n}}\)

She would like 40% of customers in the population to receive the highest possible discount, with an SEP of 0.01 for this population.

This means that \(p = 0.4, s = 0.01\)

How many coupons should she order?

We have to find n. So

\(s = \sqrt{\frac{p(1-p)}{n}}\)

\(0.01 = \sqrt{\frac{0.4*0.6}{n}}\)

\(0.01\sqrt{n} = \sqrt{0.4*0.6}\)

\(\sqrt{n} = \frac{\sqrt{0.4*0.6}}{0.01}\)

\((\sqrt{n})^2 = (\frac{\sqrt{0.4*0.6}}{0.01})^2\)

\(n = 2400\)

She should order 2400 coupons.

Answer:

Step-by-step explanation:

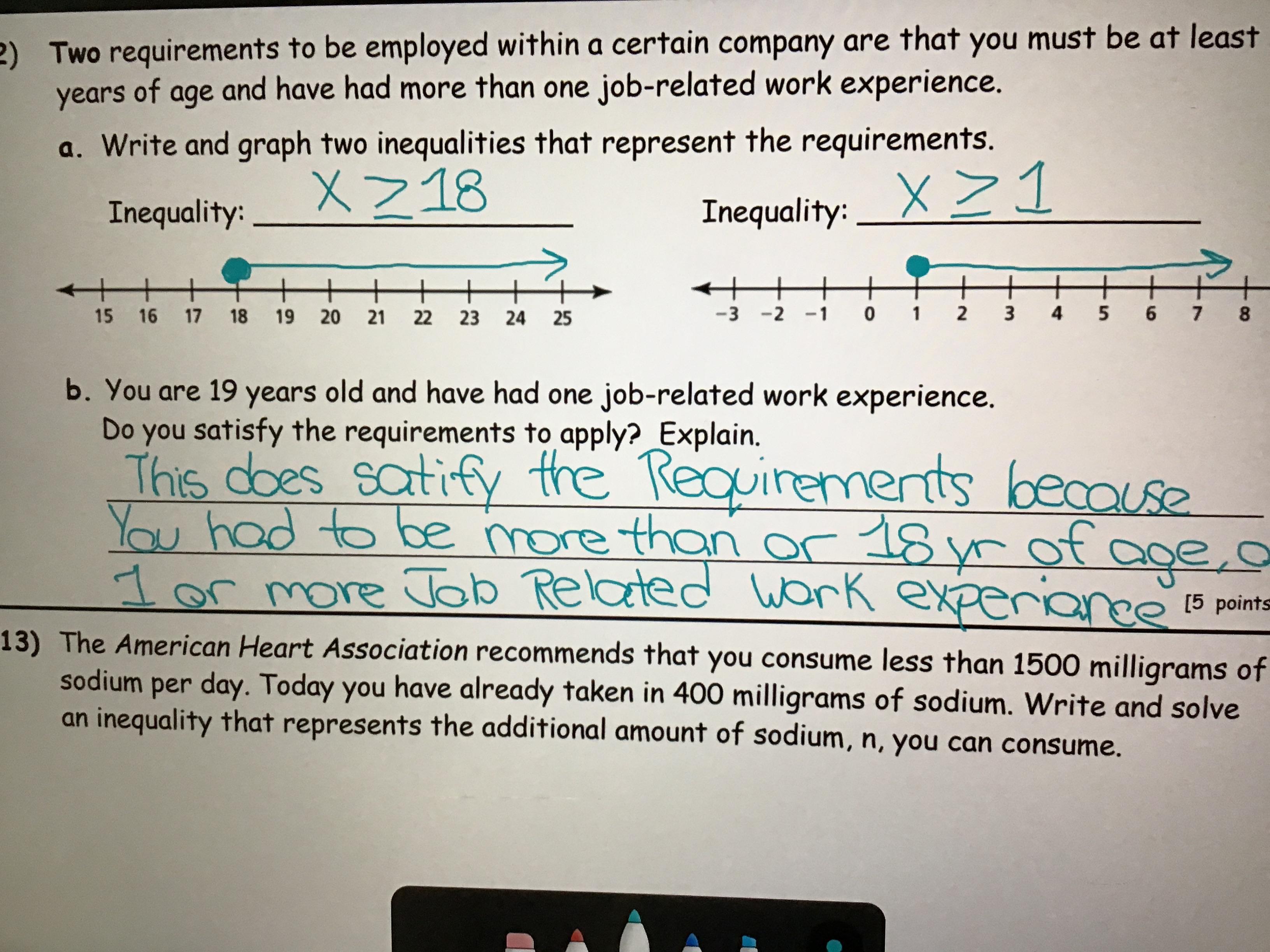
x≥18 and x>1 are the inequalities which represents certain company are that you must be at least 18 years of age and have had more than one job-related work experience.

A relationship between two expressions or values that are not equal to each other is called 'inequality.

Given,

A certain company are that you must be at least 18 years of age

Let x be the age of employees.

x must be at least 18 years of age.

x≥18

We use ≥ symbol when atleast is used, which means it can be 18 or more than that.

Now employees more than one job-related work experience

Let x be the work experience.

x>1

Here we use > because its given that it should be greater than 1.

Hence, x≥18 and x>1 are the inequalities which represents certain company are that you must be at least 18 years of age and have had more than one job-related work experience.

To learn more on Inequality click:

https://brainly.com/question/28823603

#SPJ2

Answer:

12.04

Step-by-step explanation:

Well to solve for the unknown side "c" we need to use the Pythagorean Theorem formula,

\(a^2 + b^2 = c^2\)

We already have a and b which are 8 and 9 so we plug them in.

\((8)^2 + (9)^2 = c^2\)

64 + 81 = c^2

145 = c^2

c = 12.04 rounded to the nearest hundredth.

Thus,

the unknown side is about 12.04.

Hope this helps :)

Answer:

a four-sided plane rectilinear figure with opposite sides parallel.

Step-by-step explanation:

Answer:

Parallelograms are a type of quadrilateral, which is a polygon with four sides. A parallelogram is a specific type of quadrilateral that has two pairs of parallel sides. This means that the opposite sides of a parallelogram are parallel and equal in length.

In addition to having parallel sides, parallelograms also have some other notable properties:

Opposite angles are congruent: The opposite angles of a parallelogram are equal in measure. This means that if you label the angles A, B, C, and D, then angle A is congruent to angle C, and angle B is congruent to angle D.

Step-by-step explanation:

Answer:

12

Step-by-step explanation:

3

9

(100−64)

=12

Answer:

b=64 96/149

Step-by-step explanation:

Answer: The radius of the circle is 5 3/8 inches.

Step-by-step explanation:

The radius of the circle is half of the diameter. We can start by converting the mixed number diameter to an improper fraction:

10 3/4 = (10 × 4 + 3)/4 = 43/4

So, the diameter of the circle is 43/4 inches. The radius is half of this, which we can find by dividing by 2:

r = (43/4) ÷ 2 = 43/8

To simplify the fraction, we can divide the numerator and denominator by their greatest common factor (GCF), which is 1:

r = 43/8 = 5 3/8

Therefore, the radius of the circle is 5 3/8 inches.

Answer:5 3/4

Step-by-step explanation:

10 3/4 * 1/2

1/2 * 43/4 = 43/8

8/43=5 3/4

The number of yellow pins will be 14.

Expression in maths is defined as the collection of the numbers variables and functions by using signs like addition, subtraction, multiplication, and division.

Numbers (constants), variables, operations, functions, brackets, punctuation, and grouping can all be represented by mathematical symbols, which can also be used to indicate the logical syntax's order of operations and other features.

Given that Greg ordered a set of yellow and orange pins. He received 25 pins, and 36% of them were yellow.

The number of the yellow pins will be calculated as:-

36% of the pin = ( 25x 36 ) / 64

36 % of te pin = 14

Therefore, the yellow pins will be 14 in number.

To know more about an expression follow

https://brainly.com/question/28966837

#SPJ1

The answer is:

g(x + 1) = 6x + 1

g(4x) = 24x -5

Work/explanation:

To evaluate, I plug in x + 1 into the function:

\(\sf{g(x)=6x-5}\)

\(\sf{g(x+1)=6(x+1)-5}\)

Simplify

\(\sf{g(x+1)=6x+6-5}\)

\(\sf{g(x+1)=6x+1}\)

------------------

Do the same thing with g(4x)

\(\sf{g(4x)=6(4x)-5}\)

\(\sf{g(4x)=24x-5}\)

Hence, these are the answers.

The required, general solution for x that satisfies the equation cos(x + 30) = -1 is x = (2n + 1)π - 30.

To find the general solution for the equation cos(x + 30) = -1, we can start by considering the general form of the cosine function. The cosine function has a period of 2π, meaning it repeats every 2π radians.

In this equation, we have cos(x + 30) = -1. Since the cosine function has a maximum value of 1 and a minimum value of -1, the only way for cos(x + 30) to equal -1 is if x + 30 is an odd multiple of π. We can write this as:

x + 30 = (2n + 1)π

Here, n is an integer representing the number of periods of the cosine function. To find the general solution, we can solve for x by subtracting 30 from both sides:

x = (2n + 1)π - 30

This equation gives us the general solution for x that satisfies the equation cos(x + 30) = -1. We can see that for each integer value of n, we have a different solution.

Learn more about trigonometric functions here:

https://brainly.com/question/25618616

#SPJ1