A small airplane can carry less
than 840 pounds of luggage and
mail. The mail for the day weighs
480 pounds. If each passenger
brings 60 pounds of luggage,
what is the greatest possible
number of passengers that can
be taken?
Answers
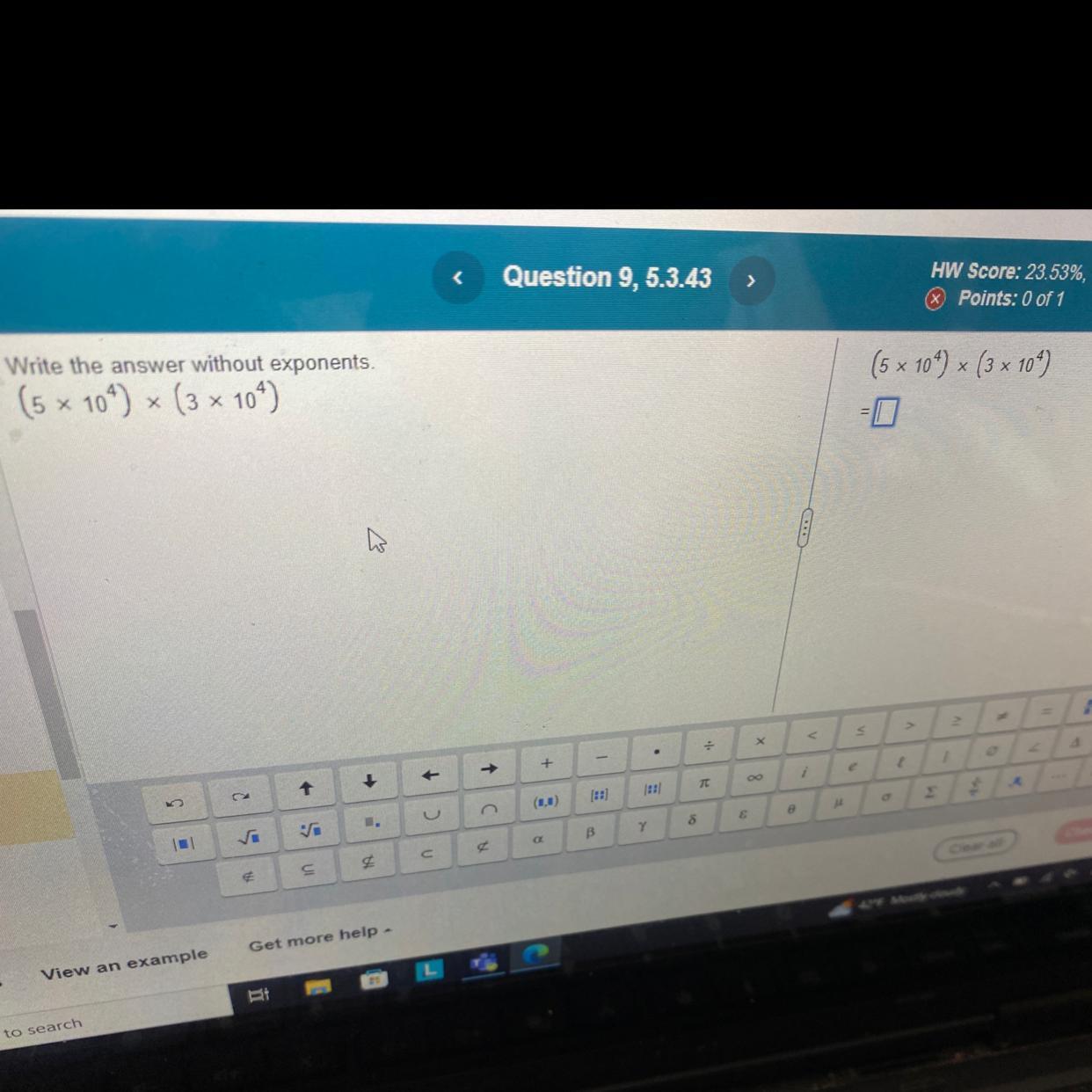
answer is x = 6
Related Questions
The fill amount of bottles of a soft drink is normally distributed, with a mean of 3.0 and a standard deviation of 0.05 liter. Suppose you select a random sample of 25 bottles .
A- The probability is 99% that the sample mean amount of soft drink will be at least how much?
B- The probability is 99% that the sample mean amount of soft drink will be between which two values (symmetrically distributed around the mean)?
Answers
The probability is 99% that the sample mean amount of soft drink will be between 2.92384 and 3.07616 liters.
What is mean?
In statistics, the mean is a measure of central tendency that represents the average value of a set of numbers. It is calculated by adding up all the values in a dataset and then dividing the sum by the total number of values.
We can use the central limit theorem (CLT) to approximate the distribution of the sample mean, which follows a normal distribution with a mean of the population mean (μ) and a standard deviation of the population standard deviation divided by the square root of the sample size (σ/√n).
Given that the population mean (μ) is 3.0 liters and the population standard deviation (σ) is 0.05 liters, we can compute the standard error of the mean as follows:
standard error of the mean = σ/√n = 0.05/√25 = 0.01 liters
A) To find the probability that the sample mean amount of soft drink will be at least a certain value, we need to convert this value into a z-score using the formula:
z = (x - μ) / (σ / √n)
where x is the sample mean we are interested in.
For a 99% probability, the corresponding z-score is 2.576 (from a standard normal distribution table). Thus, we have:
2.576 = (x - 3.0) / 0.01
Solving for x, we get:
x = 3.02576
Therefore, the probability is 99% that the sample mean amount of soft drink will be at least 3.02576 liters.
B) To find the range of values for the sample mean that contains 99% of the distribution, we can use the same approach as in part A, but for a range of values symmetrically distributed around the mean. Let's call the lower and upper limits of this range x1 and x2, respectively. Then, we have:
2.576 = (x1 - 3.0) / 0.01 and -2.576 = (x2 - 3.0) / 0.01
Solving for x1 and x2, we get:
x1 = 2.92384 and x2 = 3.07616
Therefore, the probability is 99% that the sample mean amount of soft drink will be between 2.92384 and 3.07616 liters.
To learn more about mean visit:
https://brainly.com/question/1136789
#SPJ1
Given that for an arithmetic sequence, the first term is q and the second term is qz.
(a) Find the common difference d the general term Tn and the sum of the first n terms. Answer must
be in terms of q and z.
(b) Hence, find the sum of the first 10 terms in terms of q and z.
Answers
Answer:
\(d = q(z-1)\)
\(S_n = \frac{nq}{2}(2 + (n-1)(z-1))\)
\(S_{10} = 5q(9z -7)\)
Step-by-step explanation:
Given
\(T_1 = q\)
\(T_2 = qz\)
Solving (a1): The common difference (d)
d is calculated as
\(d = T_2 - T_1\)
This gives:
\(d = qz - q\)
Factorize:
\(d = q(z-1)\)
Solving (a2): Sum of n terms
This is calculated using:
\(S_n = \frac{n}{2}(2*T_1 + (n-1)d)\)
Substitute values for T1 and d
\(S_n = \frac{n}{2}(2*q + (n-1)q(z-1))\)
\(S_n = \frac{n}{2}(2q + q(n-1)(z-1))\)
Factorize:
\(S_n = \frac{n}{2}(q(2 + (n-1)(z-1)))\)
\(S_n = \frac{nq}{2}(2 + (n-1)(z-1))\)
Solving (b): Sum of first 10.
In this case, n = 10
So:
\(S_n = \frac{nq}{2}(2 + (n-1)(z-1))\)
becomes
\(S_{10} = \frac{10 * q}{2}(2 + (10-1)(z-1))\)
\(S_{10} = 5 * q(2 + 9(z-1))\)
\(S_{10} = 5q(2 + 9(z-1))\)
\(S_{10} = 5q(2 + 9z-9)\)
\(S_{10} = 5q(2 -9+ 9z)\)
\(S_{10} = 5q(-7+ 9z)\)
\(S_{10} = 5q(9z -7)\)
Given that the first term and the second term of an arithmetic sequence is q and qz respectively, therefore:
a. Common difference (d) = \(\mathbf{d = q(z - 1)}\)
Sum of the first n terms is: \(\mathbf{S_n = \frac{qn}{2}[2 + (n - 1)(z - 1)]}\)
b. \(\mathbf{S_{10} = 5q(9z - 7)}\)
Recall:
The common difference (d) of an arithmetic sequence = difference between the next term and the previous termSum of n terms, \(S_n\) of arithmetic sequence = \(\frac{n}{2}[2a + (n - 1)d]\)Given:
First term, \(T_1 = q\) (this is also "a")Second term, \(\\\\T_2 = qz\)a. Common difference (d) = \(T_2 - T_1\)
Substitute\(d = qz - q\\\\\mathbf{d = q(z - 1)}\)
Sum of n terms:
\(T_n = \frac{n}{2}[2a + (n - 1)d]\)
Substitute by plugging in the value of d and a\(S_n = \frac{n}{2}[2(q) + (n - 1)q(z - 1)]\\\\S_n = \frac{n}{2}[2q + q(n - 1)(z - 1)]\\\\S_n = \frac{qn}{2}[2 + 1(n - 1)(z - 1)]\\\\\mathbf{S_n = \frac{qn}{2}[2 + (n - 1)(z - 1)]}\)
b. Sum of the first 10 terms:
Substitute n = 10 into \(S_n = \frac{qn}{2}[2 + (n - 1)(z - 1)]\)\(S_{10} = \frac{q(10)}{2}[2 + (10 - 1)(z - 1)]\)
Simplify\(S_{10} = 5q[2 + (9)(z - 1)]\\\\S_{10} = 5q(2 + 9z - 9)\\\\\)
Add like terms\(\mathbf{S_{10} = 5q(9z - 7)}\)
In summary, given that the first term and the second term of an arithmetic sequence is q and qz respectively, therefore:
a. Common difference (d) = \(\mathbf{d = q(z - 1)}\)
Sum of the first n terms is: \(\mathbf{S_n = \frac{qn}{2}[2 + (n - 1)(z - 1)]}\)
b. \(\mathbf{S_{10} = 5q(9z - 7)}\)
Learn more here:
https://brainly.com/question/14311840
Solve the proportion.
3x/9=7/4
Answers
Answer:
exact form: x=21/4
decimal form: 5.25.
mixed number form: x=5 1/4
Step-by-step explanation:
have a good day :)
Answer:
x = 5.25 or 21/4 or 5 1/4
Step-by-step explanation:
3x : 9 = 7 : 4
3x = 9 x 7 : 4
3x = 63 : 4
3x = 15.75
x = 15.75 : 3
x = 5.25 or 21/4 or 5 1/4
-----------------
check
(3 × 5.25) : 9 = 7 : 4
15.75 : 9 = 7 : 4
1.75 = 1.75
same value, the answer is good
What does AB congruent symbol CD mean? AB and CD here have lines over them How is it different than AB=CD?
Answers
Answer:
Suppose that we have two line segments, AB and CD. We know that they have the same length.
I know that AB¯¯¯¯¯¯¯¯=CD¯¯¯¯¯¯¯¯ means AB is identical to CD (aka. They are the same lines), and also that AB¯¯¯¯¯¯¯¯≅CD¯¯¯¯¯¯¯¯ means that AB and CD have the same size, but what does AB=CD mean?
Step-by-step explanation:
Los 1600 euros de alquiler de un terreno se reparten entre tres ganaderos que llevan alli a pastar sus ovejas. Como no tienen el mismo número de ovejas, deciden pagar proporcionalmente al número de ovejas de cada uno. Si el primero tiene 120 Ovejas,el segundo 72 y el tercero 68. ¿ Cuánto paga cada uno?
Answers
So, each farmer pays the following amounts: The first farmer pays 738.40 euros. The second farmer pays 443.04 euros. The third farmer pays 418.56 euros
What is proportion?Proportion refers to the equality of two ratios. In other words, when two ratios are set equal to each other, they form a proportion. A proportion is typically written in the form of two fractions separated by an equals sign, such as a/b = c/d. Proportions are commonly used in mathematics to solve problems involving ratios and proportions, such as finding missing values or scaling up or down a given quantity.
Here,
To find out how much each farmer pays, we need to determine the proportion of the total rent that each farmer owes based on the number of sheep they have. First, we need to find the total number of sheep:
120 + 72 + 68 = 260
The first farmer has 120 sheep, which is 46.15% of the total number of sheep (120/260). Therefore, the first farmer owes 46.15% of the rent:
0.4615 x 1600 = 738.40 euros
Similarly, the second farmer has 72 sheep, which is 27.69% of the total number of sheep (72/260). Therefore, the second farmer owes 27.69% of the rent:
0.2769 x 1600 = 443.04 euros
The third farmer has 68 sheep, which is 26.15% of the total number of sheep (68/260). Therefore, the third farmer owes 26.15% of the rent:
0.2615 x 1600 = 418.56 euros
To know more about proportion,
https://brainly.com/question/29474065
#SPJ1
Complete question:
The rent of 1600 euros for a piece of land is divided among three farmers who graze their sheep there. As they do not have the same number of sheep, they decide to pay proportionally according to the number of sheep each has. If the first one has 120 sheep, the second 72, and the third 68. How much does each one pay?
There are ten red cards in a sack and two blue cards in the same sack. How likely is it for you to draw a red card if you make one draw?
Answers
Answer:
83%
Step-by-step explanation:
I think this is the correct answer
The sum of three numbers is 99. The third number is 3 times the first . The second number is 9 more than the first. What are the numbers?
Answers
Answer: This can be written as x + (x-9) + 3(x-9) = 99
5x - 36 = 99
5x = 135
x = 135/5 = 27
You can now just plug in the value of x for each of the initial terms to get:
n1 = 27
n2 = 18
n3 = 54
Step-by-step explanation:
Evaluate 2 – 10+ 8- (-2).
Answers
Steps to solve:
2 - 10 + 8 - (-2)
~Simplify
2 - 10 + 8 + 2
~Subtract
-8 + 8 + 2
~Add
0 + 2
~Add
2
Best of Luck!
Answer:
2
Step-by-step explanation:
first you do this first (-2) then the 2 - is gone then 10 + 8- is 2
Compare using <, >, or =. 72 ___ 26
Answers
Answer:
72 > 26
Step-by-step explanation:
72 is bigger than 26
one card is drawn from a pack of 52cards each of the 52 cards being equally likely to be drawn. what is the probability that the card drawn is a king?
Answers
The probability of drawing a king from a standard deck of 52 cards is 1/13.
In a standard deck of 52 playing cards, there are four kings: the king of hearts, the king of diamonds, the king of clubs, and the king of spades.
To find the probability of drawing a king, we need to determine the ratio of favorable outcomes (drawing a king) to the total number of possible outcomes (drawing any card from the deck).
The total number of possible outcomes is 52 because there are 52 cards in the deck.
The favorable outcomes, in this case, are the four kings.
Therefore, the probability of drawing a king is given by:
Probability = (Number of favorable outcomes) / (Number of possible outcomes)
= 4 / 52
= 1 / 13
Thus, the probability of drawing a king from a standard deck of 52 cards is 1/13.
This means that out of every 13 cards drawn, on average, one of them will be a king.
It is important to note that the probability of drawing a king remains the same regardless of any previous cards that have been drawn or any other factors.
Each draw is independent, and the probability of drawing a king is constant.
For similar question on probability.
https://brainly.com/question/7965468
#SPJ8
The volume, in cubic feet, of a right cylindrical silo of height and radius is \(V = \pi r^2h\) The height of the silo is h(r) = 3.5r. Which statements are true regarding the functions described?
A. To get a volume of 100 cubic feet, the radius must be 2 feet.
B. The domain of \(V(h(r))\) is restricted to values of r greater than 0.
C. The output of V is the input of h
D. \(V(h(r)) = 3.5\pi r^3\)
E. The volume depends on the radius of the cylinder
Answers
1. The domain of \(V (h(r))\) is restricted to values of r greater than 0.
2. \(V(h(r)) = 3.5\pi r^3\)
3. The volume depends on the radius of the cylinder
Question 10 (5 points)
The graph of linear function k passes through the points (-3, 0) and (1, 8).
Which statement must be true?
O The graph of k passes through (-1,
- 8)
The zero of kis 3
The x-intercept of the graph of kis - 3
O
The slope of the graph of kis-
3
4
Please help I will give brainliest

Answers
The graph of linear function k passes through the points (-3, 0) and (1, 8) for this the true statement is given by the x-intercept of the graph of k is - 3.
As given,
Graph of the linear function k passes through the points :
(x₁ , y₁)=(-3, 0)
(x₂, y₂)=(1, 8)
Equation is given by :
(y-0)/(x+3)=(8-0)/(1+3)
⇒y=2(x+3)
⇒y=2x+6
Slope=2
X-intercept by putting y=0
x=-3
Therefore, graph of linear function k passes through the points (-3, 0) and (1, 8) for this the true statement is given by the x-intercept of the graph of
k is - 3.
Learn more about graph here
brainly.com/question/17267403
#SPJ1
help fast plz with that

Answers
Helppppppppppppppppp
Answers
Write the fraction product of a whole number and a unit fraction.
5/12
Answers
Answer:
5*1/12
Step-by-step explanation:
I don't know if this is right but hopefully it is ^^"
Please help I’ll give brainliest

Answers
Answer:
ITS D GOOD LUCK WITH YOUR HMK
Check all the statements) that are true about the polynomial function graphed
Its leading coefficient is positive. its leading coefficient is negative.
It has an odd degree
It has an even degree
It has exactlv two real zeroes
It has exactly three real zeroes.
None of the zeroes have even multiplicity
None of the zeroes have odd multiplicity.
Answers
The true statements about the polynomial function graphed are:
Its leading coefficient is positive.
It has an odd degree.
None of the zeroes have even multiplicity.
From the given options, the true statements about the polynomial function graphed are:
Its leading coefficient is positive.
It has an odd degree.
None of the zeroes have even multiplicity.
Let's analyze each statement:
Its leading coefficient is positive:
The leading coefficient of a polynomial is the coefficient of the term with the highest degree.
From the graph, if the polynomial is going upwards on the right side, it indicates that the leading coefficient is positive.
It has an odd degree: The degree of a polynomial is the highest power of the variable in the polynomial expression.
If the graph has an odd number of "turns" or "bumps," it indicates that the polynomial has an odd degree.
None of the zeroes have even multiplicity:
The multiplicity of a zero refers to the number of times it appears as a factor in the polynomial.
In the given graph, if there are no repeated x-intercepts or no points where the graph touches and stays on the x-axis, it implies that none of the zeroes have even multiplicity.
The other statements (its leading coefficient is negative, it has an even degree, it has exactly two real zeroes, it has exactly three real zeroes, and none of the zeroes have odd multiplicity) cannot be determined based solely on the information given.
Therefore, the true statements about the polynomial function graphed are:
Its leading coefficient is positive.
It has an odd degree.
None of the zeroes have even multiplicity.
For similar question on polynomial function.
https://brainly.com/question/31528136
#SPJ8
Please answer number 4 please!

Answers
Hope this helps.
I believe the answer is A.
If the largest of 89 consecutive integers is 324, what is the smallest?
Answers
Answer:
Step-by-step explanation:
If the larger of 2 consecutive integers is 324, then 324-(2-1) = 323 is the smaller.
If the largest of 89 consecutive integers is 324, then 324 - (89-1) = 236 is the smallest.
Hence, the smallest consecutive integer is \(237\).
What is the smallest consecutive integer?
Numbers that follow each other continuously in the order from smallest to largest are called consecutive numbers.
Here given that,
The largest of \(89\) consecutive integers is \(324\)
So, it is of the form
\(324-89=237\)
Hence, the smallest consecutive integer is \(237\).
To know more about the smallest consecutive integer
https://brainly.com/question/10537962
#SPJ2
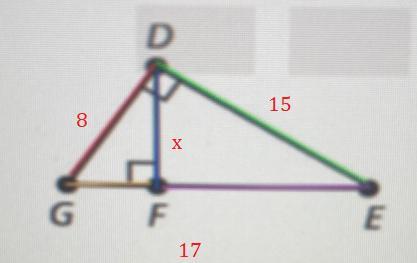
In DGE, DG = 8, GE = 17, and DE = 15. What is the length of DF? Round to the nearest hundred

Answers
Answer:
7.06 units
Explanation:
The given side lengths are indicated in the diagram below:
Using similar triangles, we have:
\(\begin{gathered} \frac{GF}{8}=\frac{8}{17} \\ 17GF=64 \\ GF=\frac{64}{17} \\ GF=3.76 \end{gathered}\)Next, apply Pythagorean Theorem to triangle DGF.
\(\begin{gathered} DG^2=DF^2+GF^2 \\ 8^2=DF^2+3.76^2 \\ DF^2=8^2-3.76^2 \\ DF^2=49.8624 \\ DF^{}=\sqrt{49.8624} \\ DF\approx7.06\text{ units} \end{gathered}\)The length of DF is approximately 7.06 units (to the nearest hundred).
Find the unknown angle measure.

Answers
Answer:
54
Step-by-step explanation:
equilateral triangle= 2 angles equal
180-72=108
108/2 =54
x=54
If other factors are held constant, how does sample size influence the likelihood of rejecting the null hypothesis and measures of effect size such as r^2 and Cohen's d?A) A larger sample increases both the likelihood and measures of effect size.B) A larger sample increases the likelihood but has little influence on measures of effect size.C) A larger sample decreases the likelihood but has little influence on measures of effect size.D) A larger sample decreases both the likelihood and measures of effect size.
Answers
Answer:
2000
Step-by-step explanation:
the first number of a pattern is 177. the pattern follows the "subtract 28" rule. what are the next two numbers?
Answers
We were told that the first number is 177. if it follows the "subtract 28" rule, it means that
The second number would be 177 - 28 = 149
The third number would be 149 - 28 = 121
The next two numbers are 149 and 121
NOT SURE HELPP... it's a khan academy question

Answers
Answer:
36.87
Step-by-step explanation:
Sine rules says:
. sin x = opposite / hypotenuse
We just substitute in the values
. sin x = 3 / 5
. sin x = 0.6
Now we use sin inverse to find the value of the angle
. x = sin^-1(0.6) = 36.87
\(\sin \angle A = \dfrac{3}{5} \\\\\implies \angle A = \sin^{-1} \left( \dfrac 35 \right) = 36.87^{\circ}\)
Pls help for points

Answers
Answer:
The Answer is 1331
Step-by-step explanation:
11*11*11
The retail price for Jamaican allspice is $4.69 per ounce. You buy 8 ounces of allspice on sale for $4.62 per ounce. How much money do you save?
Answers
Answer:
Step-by-step explanation
56 cents
Explanation: The deal is 7 cents less per ounce, you need to buy 8 ounces, multiply 7 by 8, equaling 56 cents
Wesson Company sold 10,000 units of its only product in the first half of the year. If sales increase by 12% in the second half of the year, which cost will increase?
Answers
Answer:
Direct materials
Step-by-step explanation:
In this case we must bear in mind that as more products are sold, more material is needed to manufacture those additional final products
.
Therefore, in this case the cost would be related mainly to the materials, mainly the direct materials, since they are essential in the production of the product.
Factorize q2-4 completely
Answers
The completely factorized form of the expression q² - 4 is (q + 2)(q - 2).
What is the factored form of the expression?Given the expression in the question:
q² - 4
To factorize the expression q² - 4 completely, we can use the formula for the difference of squares.
The difference of squares formula states that :
a² - b² can be factored as (a + b)(a - b).
Given that:
q² - 4
Replace 4 with 2²
q² - 2²
From this expression, let a = x and b = 2
a² - b² = (a + b)(a - b)
q² - 2² = (q + 2)(q - 2)
Therefore, the factored form is (q + 2)(q - 2).
Learn more about the difference of squares here: https://brainly.com/question/30186712
#SPJ1
David and Ken took part in a cycling race. Both of them did not change their speed throughout the race. David completed the race in 5 hours while Ken took 7 hours. Ken's average speed was 9.8 km/h less than David's average speed.
A) What was David average speed
B)What was the distance of the cycling race?
Answers
Let's assume David's average speed is S km/h.
A) To find David's average speed, we can use the formula: Speed = Distance / Time.
David completed the race in 5 hours, so his speed is S km/h. Therefore, we have:
S = Distance / 5
B) Ken's average speed is 9.8 km/h less than David's average speed, which means Ken's average speed is (S - 9.8) km/h.
Ken took 7 hours to complete the race, so we have:
S - 9.8 = Distance / 7
Now, we can solve the system of equations to find the values of S and Distance.
From equation (1): S = Distance / 5
Substitute this into equation (2):
Distance / 5 - 9.8 = Distance / 7
Multiply both sides of the equation by 35 to eliminate the denominators:
7 * Distance - 35 * 9.8 = 5 * Distance
7 * Distance - 343 = 5 * Distance
Subtract 5 * Distance from both sides:
2 * Distance - 343 = 0
Add 343 to both sides:
2 * Distance = 343
Divide both sides by 2:
Distance = 343 / 2 = 171.5 km
Therefore, the distance of the cycling race is 171.5 kilometers.
To find David's average speed, substitute the distance into equation (1):
S = Distance / 5 = 171.5 / 5 = 34.3 km/h
So, David's average speed was 34.3 km/h.\(\)
Answer:
A) 34.3 km/h
B) 171.5 km
Step-by-step explanation:
Since Ken's average speed is said to be 9.8km/h less than David's average speed, and we know that Ken's average speed is dependent on him traveling for 7 hours, then we have our equation to get the distance of the cycling race:
\(\text{Ken's Avg. Speed}=\text{David's Avg. Speed}\,-\,9.8\\\\\frac{\text{Distance}}{7}=\frac{\text{Distance}}{5}-9.8\\\\\frac{5(\text{Distance})}{7}=\text{Distance}-49\\\\5(\text{Distance})=7(\text{Distance})-343\\\\-2(\text{Distance})=-343\\\\\text{Distance}=171.5\text{ km}\)
This distance for the cycling race can now be used to determine David's average speed:
\(\text{David's Avg. Speed}=\frac{\text{Distance}}{5}=\frac{171.5}{5}=34.3\text{ km/h}\)
Therefore, David's average speed was 34.3 km/h and the distance of the cycling race was 171.5 km.
Wanna eat some sushi?
Answers
Answer: sure why not
Step-by-step explanation: