A sample of 1 can be drawn from an automatic storage and retrieval rack with 9 different storage racks and 6 different trays in each rack, find the number of different ways of obtaining a tray?
Answers
There are 54 different ways of obtaining a tray from the automatic storage and retrieval rack.
To find the number of different ways of obtaining a tray from an automatic storage and retrieval rack, we can use the concept of the multiplication principle.
The multiplication principle states that if there are m ways to do one thing and n ways to do another thing, then there are m × n ways to do both things together.
In this case, we have two steps involved in obtaining a tray:
Selecting a storage rack: There are 9 different storage racks available. We can choose any one of them.
Selecting a tray within the chosen storage rack: Once we have chosen a storage rack, there are 6 different trays in each rack. We can select any one of these trays.
According to the multiplication principle, the total number of ways to perform both steps is the product of the number of options for each step.
Number of ways = Number of options for Step 1 × Number of options for Step 2
= 9 × 6
= 54
Therefore, there are 54 different ways of obtaining a tray from the automatic storage and retrieval rack.
Learn more about multiplication principle here:
https://brainly.com/question/11514947
#SPJ11
Related Questions
using the information above, choose the correct conclusion that interprets the results within the context of the hypothesis test.
Select the correct answer bellow:
a. We should reject the null hypothesis because to < tn, So, at the 10% significance level, the data provide sufficient evidence to conclude that the averege percentege of tips recieved waitstaff in Chicago restaurants is less than 15%
b. We should do not reject the null hypothesis because to < tn, So, at the 10% significance level, the data do not provide sufficient evidence to conclude that the averege percentege of tips recieved waitstaff in Chicago restaurants is less than 15%
c. We should not reject the null hypothesis because to > tn, So, at the 10% significance level, the data do not provide sufficient evidence to conclude that the averege percentege of tips recieved waitstaff in Chicago restaurants is less than 15%
d. We should do not reject the null hypothesis because to > tn, So, at the 10% significance level, the data do not provide sufficient evidence to conclude that the averege percentege of tips recieved waitstaff in Chicago restaurants is less than 15%
Answers
The correct conclusion that interprets the results within the context of the hypothesis test is that "We should not reject the null hypothesis because to > tn.(C)
So, at the 10% significance level, the data do not provide sufficient evidence to conclude that the average percentage of tips received by waitstaff in Chicago restaurants is less than 15%."
In hypothesis testing, the null hypothesis assumes that there is no significant difference between the observed and expected data. (C)
The alternative hypothesis suggests otherwise and will be used to determine the significance level. In this case, the average percentage of tips received by waitstaff in Chicago restaurants is less than 15%.
To interpret the result, the t-value is compared to the critical value. When the t-value is greater than the critical value, the null hypothesis is rejected. If the t-value is less than the critical value, the null hypothesis is not rejected. In this case, the t-value is less than the critical value, and thus, the null hypothesis is not rejected.
Therefore, at the 10% significance level, there is no sufficient evidence to conclude that the average percentage of tips received by waitstaff in Chicago restaurants is less than 15%.
To know more about null hypothesis click on below link:
https://brainly.com/question/28920252#
#SPJ11
Given the that the speed of light in a vacuum is about 3.0x10 to the power of 8 meters per second how far does light travel in two weeks
using scientific notation
Answers
The distance covered by light in 2 weeks is \(3.6288*10^{14}\) m.
It is given that:-
Speed of light = \(3*10^8 m/s\)
We have to find the distance travelled by the light in 2 weeks.
We know that,
1 week = 7 days
Hence,
2 weeks = 14 days
Also,
1 day = 24 hours
1 hour = 60 minutes
1 min = 60 seconds
Hence, we can write,
1 day = 60*60*24 seconds = 86,400 seconds
14 days = 86400*14 = 12,09,600 seconds
We know that,
Speed = distance/time
Hence,
distance = speed * time
Hence, distance travelled by light in 2 weeks = \(3*10^8*1209600 = 3628800 * 10^8 = 3.6288*10^{14} m\)
To learn more about Speed of light, here:-
https://brainly.com/question/394103
#SPJ1
what is the equation in slope intercept form of the line that passes through the point (2,-5) and is parallel to the line represented by 8x+2y=14
Answers
Answer: y = -4x + 3
Step-by-step explanation:
First, we will write 8x+2y=14 in slope-intercept form.
8x+2y=14
2y = -8x + 14
y = -4x + 7
Next, we will take this new slope-intercept form equation, y = -4x + 7, and use the slope from it to substitute the coordinate point given to find the y-intercept of the equation we are trying to find.
y = -4x + b
(-5) = -4(2) + b
-5 = -8 + b
b = 3
Lastly, we will write our equation with a slope of -4 and a y-intercept of 3.
y = -4x + 3

Given ABC with AB=3,BC=5,and CA=6 find the length of a mid segment XY

Answers
Answer:
\( \overline{XY} = 1.5 \)
Step-by-step explanation:
Given:
AB = 3
BC = 5
CA = 6
Required:
Length of XY
SOLUTION:
According to the Triangle Midsegment Conjecture, midsegment \( \overline{XY} \) is half the length of \( \overline{AB} \).
Therefore:
\( \overline{XY} = \frac{1}{2}(\overline{AB}) \)
Thus:
\( \overline{XY} = \frac{1}{2}(3) \)
\( \overline{XY} = \frac{3}{2} \)
\( \overline{XY} = 1.5 \)
in a circle, a sector with central angle is 225 degrees intercepts an arc of length 30pi in. find the diameter of the circle
Answers
The diameter of the circle is approximately 60 inches.
To explain further, we can use the formula relating the central angle of a sector to the length of its intercepted arc. The formula states that the length of the intercepted arc (A) is equal to the radius (r) multiplied by the central angle (θ) in radians.
In this case, we are given the central angle (225 degrees) and the length of the intercepted arc (30π inches).
To find the diameter (d) of the circle, we need to find the radius (r) first. Since the length of the intercepted arc is equal to the radius multiplied by the central angle, we can set up the equation 30π = r * (225π/180). Simplifying this equation gives us r = 20 inches.
The diameter of the circle is twice the radius, so the diameter is equal to 2 * 20 inches, which is 40 inches. Therefore, the diameter of the circle is approximately 60 inches.
In summary, by using the formula for the relationship between central angle and intercepted arc length, we can determine the radius of the circle. Doubling the radius gives us the diameter, which is approximately 60 inches.
for such more questions on diameter
https://brainly.com/question/30460318
#SPJ8
Which object has a capacity that is best measured in pints
1.swimming pool
2. Water Bottle
3. Soup Spoon
4.Trash Barrel
HURRY PLZ I WILL GIVE U BRAINLEST
Answers
A. (3,1)
B. (3,-1)
C. (-3,-1)
D.(-3,1)

Answers
Step-by-step explanation:
D) (-3, 1)
I is 3 steps away from the y axis, so counting 3 steps further you'll have (-3,1)
Y= 3y - 2x
2y = 3x -2
(método de sustitución, igualación y suma y resta)
Answers
The solution of the system of equations is (x, y) = (1/3, 1/3).
To solve the given system of equations, we can use any of the following three methods; the substitution method, the elimination method (also known as the addition/subtraction method), and the graphical method. Below, we will solve it using each of these methods.
1. Substitution method:
We will use the substitution method to solve the system of equations. Step-by-step solution is shown below; Given equations are
Y = 3y - 2x ...(1)2y = 3x - 2 ...(2) From equation (1), we have
Y + 2x = 3y ...(3)Now substitute equation (3) into equation
(2)2y = 3x - 2 ...(2)Y + 2x = 3y ...(3)2(3y - 2x) = 3x - 2
Multiplying both sides by 2:
6y - 4x = 3x - 2 Grouping like terms:
6y - 3x = 2 Adding 3x to both sides:
6y = 3x + 2Dividing both sides by 6:
y = (3/6)x + 2/6y = (1/2)x + 1/3
Therefore, the solution of the system of equations is (x, y) = (1/3, 1/3).
2. Elimination method:
We will use the elimination method to solve the system of equations. Step-by-step solution is shown below; Given equations are
Y = 3y - 2x ...(1)2y = 3x - 2 ...(2)Multiplying equation (1) by 2,
we get;2Y = 6y - 4x ...(3)Multiplying equation (2)
by -3, we get;-6y = -9x + 6 ...(4) Adding equations (3) and (4),
we get;-4x = -9x + 8
Simplifying;-4x + 9x = 8x = -8x = -2
Therefore, we found the value of x, which is -2.
Substitute the value of x in either equation (1) or (2);
If we substitute x = -2 in equation (1), we get;
Y = 3y - 2(-2)Y = 3y + 4Y - 3y = 4Y = 4/2Y = 2Substitute the value of y in equation (1)
;Y = 3y - 2xY = 3(2) - 2(-2)Y = 6 + 4Y = 10
Therefore, the solution of the system of equations is (x, y) = (-2, 10/2).3.
For more question equations
https://brainly.com/question/4909706
#SPJ8
20) Find angle Dd= 54.9 cm, f= 69.2 cm, F = 56°

Answers
Using sine rule formula to resolve the value for angle D
The sine rule formula is,
\(\frac{sinD}{d}=\frac{sinF}{f}\)Given:
\(\begin{gathered} d=54.9cm \\ f=69.2cm \\ F=56^0 \end{gathered}\)Therefore,
\(\frac{sinD}{54.9}=\frac{sin56^0}{69.2}\)Simplify
\(\begin{gathered} sinD=\frac{54.9\times sin56^0}{69.2}=0.65771911464 \\ D=sin^{-1}(0.65771911464)=41.12615063003\approx41^0(nearest\text{ degree\rparen} \\ D=41^0 \end{gathered}\)Hence, the answer is
\(\angle D=41^0\)Please help for section d) 100 points, must show all working and step by step

Answers
Answer:
Step-by-step explanation:
(a) and (b) see diagram
(c) you can see from the graph, the purple line hits the parabola twice which is y=6 or k=6
(d) Solving simultaneously can mean to set equal
6x - x² = k >subtract k from both sides
6x - x² - k = 0 >put in standard form
- x² + 6x - k = 0 >divide both sides by a -1
x² - 6x + k = 0
(e) The new equation is the same as the original equation just flipped (see image)
(f) The discriminant is the part of the quadratic equation that is under the root. (not sure if they wanted the discriminant of new equation or orginal. I chose new)
discriminant formula = b² - 4ac
equation: x² - 6x + 6 = 0 a = 1 b=-6 c = 6
discriminant = b² - 4ac
discriminant= (-6)² - 4(1)(6)
discriminant = 36-24
discriminant = 12
Because the discriminant is positive, if you put it back in to the quadratic equation, you will get 2 real solutions.

which of the following statements about the data structures are true? select all correct answers. group of answer choices pandas can store heterogeneous data, meaning different columns in a dataframe can have different data types
Answers
The data structures are true: Option (1,3)
Pandas can store heterogeneous data, meaning different columns in a DataFrame can have different data types Numpy arrays can store homogeneous data only. That's one of the reasons why calculations with numpy arrays are so efficient.Data structures are ways of organizing and storing data in a computer so that it can be accessed and manipulated efficiently. There are several types of data structures, including arrays, linked lists, stacks, queues, trees, and graphs. Each structure has its own unique features and advantages, making it suitable for different scenarios.
For example, arrays are used for storing and accessing data in a linear fashion, while trees and graphs are used for representing hierarchical relationships between data. Data structures are a fundamental concept in computer science and are used in many applications, including databases, compilers, and operating systems. Understanding and implementing data structures is essential for efficient programming and software development
Learn more about data structures
https://brainly.com/question/12963740
#SPJ4
Full Question: Which of the following statements about the data structures are true? Select ALL CORRECT answers.
Pandas can store heterogeneous data, meaning different columns in a dataframe can have different data types Numpy arrays can store heterogeneous data. That's one of the reasons why calculations with numpy arrays are so efficient Numpy arrays can store homogeneous data only. That's one of the reasons why calculations with numpy arrays are so efficient. Pandas can store heterogeneous data, meaning different elements in a series can have different data typesTyson has a $50 gift card to use at a store. He does not have any additional money to spend at the store. Tyson will purchase a belt that costs $8 and x
number of shirts that cost $15 each. The function f(x) = 42 - 15x models the balance on the gift card after Tyson makes the purchases. What is the mo
appropriate domain of the function?
(A) all integer values of
B
all positive integer values of x
©
0 x< 2 where x is an integer
D
0<x<3 where x is an integer
First
Back Pause I
Next
Review I
Answers
0 ≤ x < 2, where x is an integer. Option C
The appropriate domain for the function f(x) = 42 - 15x in the given context can be determined by considering the constraints of the problem.
Tyson has a $50 gift card, and he wants to purchase a belt that costs $8 and x number of shirts that cost $15 each. The function f(x) represents the balance on the gift card after Tyson makes the purchases.
The number of shirts Tyson can purchase depends on the remaining balance on the gift card. Since each shirt costs $15, the maximum number of shirts he can buy is limited by the amount of money left on the gift card.
If we subtract the cost of the belt ($8) and the cost of x shirts ($15x) from the initial balance ($50), we should get a non-negative result, indicating that Tyson has enough money on the gift card to make the purchases.
Therefore, we can set up the inequality:
50 - 8 - 15x ≥ 0
Simplifying, we have:
42 - 15x ≥ 0
Now, we can solve for x:
-15x ≥ -42
Dividing by -15 (remembering to flip the inequality sign), we get:
x ≤ 42/15
x ≤ 2.8
Since x represents the number of shirts Tyson can buy, it should be a whole number. Therefore, the appropriate domain for the function f(x) is:
0 ≤ x ≤ 2, where x is an integer.
Option C.
For more such questions on integer visit:
https://brainly.com/question/929808
#SPJ8
Look over Chuck's work What is incorrect about the way Chuck interpreted his problem? What should have been a clue to Chuck that something was wrong?

Answers
The probability that a random student will be taking both Algebra 2 and Chemistry is 0.0136 or 1.36%.
To find the probability that a random student will be taking both Algebra 2 and Chemistry, we need to use the concept of conditional probability.
Let's denote the event of taking Algebra 2 as A and the event of taking Chemistry as C. We are given that P(A) = 0.08 (8% probability of taking Algebra 2) and P(C|A) = 0.17 (17% probability of taking Chemistry given that the student is taking Algebra 2).
The probability of taking both Algebra 2 and Chemistry can be calculated using the formula for conditional probability:
P(A and C) = P(C|A) * P(A)
Substituting the given values:
P(A and C) = 0.17 * 0.08
P(A and C) = 0.0136
Therefore, the probability that a random student will be taking both Algebra 2 and Chemistry is 0.0136 or 1.36%.
It is important to note that the probability of taking both Algebra 2 and Chemistry is determined by the intersection of the two events, which means students who are taking both courses. In this case, the probability is relatively low, as it depends on the individual probabilities of each course and the conditional probability given that a student is taking Algebra 2.
For more such questions on probability visit:
https://brainly.com/question/25839839
#SPJ8
What is the slope and the y-intercept of the graph of the linear function shown on the grid ?

Answers
Answer:
Slope: -1/4; Y-Intercept: 1.5
Step-by-step explanation:
Step 1: Find the slope. The best way to do this is to transform the two given points to y=mx+b form. When given two points, the best way to find the slope will be to do y2-y1/x2-x1. In this equation it would be -2-0/2+6, which is -2/8, simplified is -0.25 or -1/4. So we have the slope, which can determine the length of the line.
Step 2: Find the Y-Intercept. Finding the Y-intercept is so much simpler when given a graph, since all you have to do is find where the line goes through the y-axis, which in this case is (0,1.5), meaning that the y-intercept is 1.5 (note: the y-intercept can also be found when x=0, for example (0,9).
Hope this helped, good luck!
Please help this is due in a few Brainliest will be rewarded!!!!!

Answers
Step-by-step explanation:
the middle one has to be the same for both part ratios.
the best here is to bring the ratio element of B in the first part ratio to 10. we need to double the B element there
for that (as a ratio is a fraction) we also have to adapt the A element in the same way.
so, we get
4×2 : 5×2 : 9 =
= 8 : 10 : 9
and that is also shown in the graphic.
Answer:
X:Y:Z= 8:10:9
Step-by-step explanation:
Let x be the number of students in class A
Let y be the number of students in class B
Let z be the number of students in class C
x:y = 4:5
y:z= 10: 9
x:y:z = ?
Find the LCM of the y terms (5 and 10 ) which is 10
Divide 10 by the first y term (5) = 2
Divide 10 by the second y term(10) = 1
X: y = (4 x 2) :(5 x 2)= 8:10
y:z =(10 x 1) : (9:1)= 10:9
x:y:z= 8:10:9
I WILL MARK BRAINLIEST TO MORE THAN ONE PERSON WHO HELPS
5)Suppose that the equation N(t)=500(0.02)^(0.7t) represents the number of employees working t years after a company begins operations. a) how many employees are there when the company opens (at t=0). b)how long until there are at least 100 employees working? c) according to this model as t gets larger(and heads towards+infinite) what value does N approach? That is in the long term, how many employees will be working at this company, according to this model?
Answers
Step-by-step explanation:
Given
No. of employees \(N(t)=500(0.02)^{0.7^{t}}\)
(a)When the company opens i.e. at t=0
\(N(0)=500(0.02)^{1}=10\)
There are 10 employees at the beginning
(b)when N=100
\(100=500(0.02)^{0.7^{t}}\\0.2=0.02^{0.7^{t}}\)
Taking log both sides
\(\ln (0.2)=0.7^t \cdot \ln (0.02)\)
\(0.7^t=\frac{\ln (0.2)}{\ln (0.02)}=0.4114\)
again taking log
\(t\times \ln (0.7)=\ln (0.4114)\)
\(t=\dfrac{\ln (0.4114)}{\ln (0.7)}=2.49\)
(c)when t tends to \(\infty\), \((0.7)^t\rightarrow 0\)
So, \(N(\infty)=500\cdot(0.02)^0=500\times1=500\)
i.e. there can be 500 employees at max
a meat pie contains chicken and turkey in the ratio 4:1. The pie contains 200g of Chicken. How much turkey is in the pie?
Answers
Answer:
50 grams
Step-by-step explanation:
From the above question:
Chicken : Turkey
= 4:1
Sum Proportions = 4 + 1 = 5
We have to find the weight in grams of the entire pie
Let us represent the weight in grams of the entire pie = x.
The pie contains 200g of Chicken.
Hence:
4/5 × x = 200g
4x/5 = 200g
Cross Multiply
4x = 200g × 5
x = 200g × 5/4
x = 250g
The amount turkey that is in the pie is calculated as:
Total weight of pie - Amount of Chicken in the pie
= 250g - 200g
= 50 g
can someone answer not just use my points

Answers
Answer:
35
Step-by-step explanation:
Well if m<YVW = (12x-1) and x=3 then just plug in x
So,
m<YVW = (12(3)-1)
m<YVW = 36-1
m<YVW = 35
Please help me. It's literally math!
Find the exact two values for this problem in radians.
\(Cos x = 1/3\)
Answers
Answer:
see below
Step-by-step explanation:
given function: \(Cos(x)=\frac{1}{3}\)
------------------------------------------------------------------------------------------------------Cosine - (In a right triangle, the ratio of the length of the adjacent side to the length of the hypotenuse.)
---------------------------------------------------------------------------------------------------#1: Take the inverse cosine of both sides of the equation to extract \(x\) from inside the cosine.
\(x=arccos\frac{1}{3}\)
#2: Evaluate
\(x=1.23095941\)
#3: The cosine function is positive in the first and fourth quadrants. To find the second solution, subtract the reference angle from \(2\)π to find the solution in the fourth quadrant.
\(x=2(3.14159265)-1.23095941\)
#4: Simplify the equation above.
- Multiply \(2\) by \(3.14159265\)
\(x=6.2831853-1.23095941\)
- Subtract \(1.23095941\) from \(6.2831853\)
\(x=5.05222588\)
#5: Find the period.
- The period of the function can be calculated using \(\frac{2\pi }{|b|}\).
\(\frac{2\pi }{|b|}\)
- Replace \(b\) with \(1\) in the formula for period.
\(\frac{2\pi }{|1|}\)
#6: Solve the equation.
- The absolute value is the distance between a number and zero. The distance between \(0\) and \(1\) is \(1\).
\(\frac{2\pi }{1}\)
- Divide \(2\pi\) by \(1.\)
\(2\pi\)
The period of the \(cos(x)\) function is \(2\pi\) so values will repeat every \(2\pi\) radians in both directions.
\(x=1.23095941+2\pi n,5.05222588+2\pi n\), for any integer \(n\)
find the measure of angle A
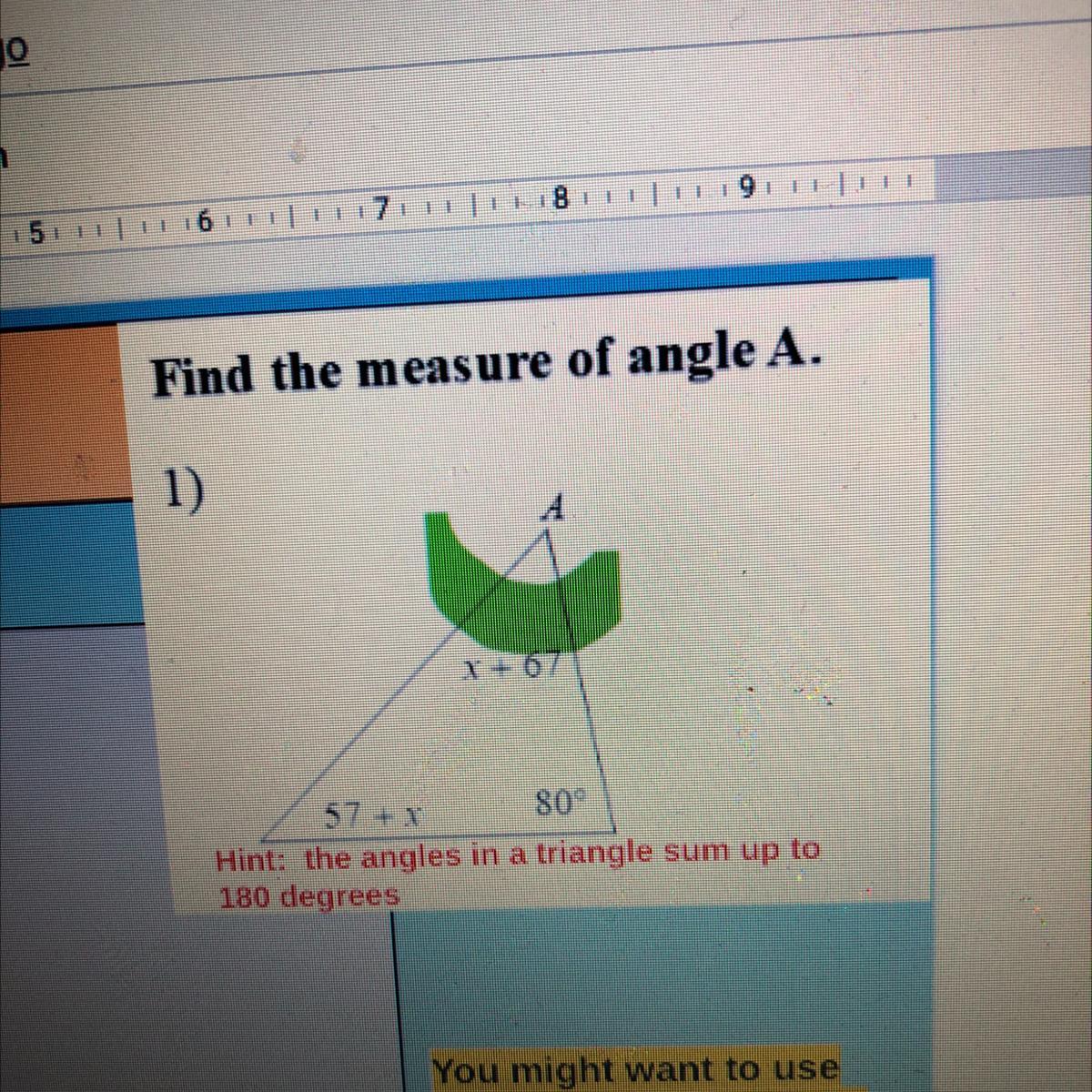
Answers
Answer:
55
Step-by-step explanation:
all angles shoudl equal 180. 180-80=100// 100= (x+67)+(x+57)// 100=2x+124// -24=2x//x=-12// -12+67= 55
8. Sam packed 15 boxes in 5 days. Dylan packed 60 boxes 4 weeks and 2 days. Who packed the most
boxes in the least in the least amount of time? Find each unit rate.
Answers
Answer:
sam did the most
Step-by-step explanation:
let's find box packed per day
sam - 15 boxes in 5 days
so 3 boxes in 1 day
Dylan - 60 boxes in 4 weeks and 2 days
that is 60 in 30 days
that will make 2 boxes in 1 day
4.5 is 75% of what number
Answers
Answer:
The answer is 6
Step-by-step explanation:
4.5 = 75% × Y
4.5 =
75
100
× Y
Multiplying both sides by 100 and dividing both sides of the equation by 75 we will arrive at:
Y = 4.5 ×
100
75
Y = 4.5 × 100 ÷ 75
Y = 6
what is the largest area of a rectangle that can be inscribed in a semicircle of radius 6? round to the nearest whole numb
Answers
The area of the largest rectangle is 46.47 square root.
Consider a semi-circle with a rectangle ABCD inscribed in it.
Let, O = centre of the semi-circle
A and B lies on the base of the semi-circle
OA = OB = x
D and C lie on the semi-circle
BC = AD = y
AB = CD = 2x
By Pythagorean theorem,
CB² + OB² = OC²
⇒ y² + x² = (6)²
⇒ y² = 36 - x²
⇒ y = √(36 - x²)
Now, area of rectangle in terms of x,
Area, A = 2x × y
= 2x × √(36 - x²)
Differentiating,
A' = 2 × √(36 - x²) - 2x²/(36 - x²)
When x = 0, y = 6 and when x = 6, y = 0, area = 0.
It implies that area is maximum when the value of x lies between 0 and 6.
This will occur where A’ = 0.
⇒ 2 × √(36 - x²) - 2x²/(36 - x²) = 0
⇒ 2 × √(36 - x²) = 2x²/(36 - x²)
On simplification, we get,
⇒ 2 × (36 - x²) = 2x²
⇒ 36 - x² = x²
⇒ 2x² = 36
⇒ x² = 36/2
⇒ x = √36/2
Now, y = √(36 - x²) becomes
⇒ y = √(36 - (√36/2)²)
⇒ y = √(36 - 36/2)
⇒ y = √(96 - 36)/2
⇒ y = √60/2
Maximum area = 2xy
= 2(√36/2)(√60/2)
= 46.47
Therefore, the area of the largest rectangle = 46.47 square units.
Learn more about Rectangles here:
brainly.com/question/24571594
#SPJ4
Camilla entered the following group of values into the TVM Solver of her
graphing calculator. N = 24,1% = 1.2, PV = PMT = -480; FV = 0P/Y = 12; C/Y
= 12, PMT-END. Which of these problems could she be trying to solve?
O A. A person can afford a $480-per-month loan payment. If she is
being offered a 24-year loan with an APR of 1.2%, compounded
monthly, what is the most money that she can borrow?
O B. A person can afford a $480-per-month loan payment. If she is
being offered a 24-year loan with an APR of 14.4%, compounded
monthly, what is the most money that she can borrow?
O C. A person can afford a $480-per-month loan payment. If she is
being offered a 2-year loan with an APR of 14.4%, compounded
monthly, what is the most money that she can borrow?
D. A person can afford a $480-per-month loan payment. If she is
being offered a 2-year loan with an APR of 1.2%, compounded
monthly, what is the most money that she can borrow?
Answers
The problem that Camilla could she be trying to solve is D. a person can afford a $480-per-month loan payment.
What is a loan?It should be noted that a loan simply means an amount of money that's taken for future repayment.
In this case, the information given shows that the problem will be that the person can afford a $480-per-month loan payment and she is being offered a 2-year loan with an APR of 1.2%, compounded monthly.
Learn more about loan on:
https://brainly.com/question/26011426
One letter is chosen at random from the word THANKS. A letter is then chosen at random from the word STARK
1. Write out ALL of the outcomes in the sample space of this chance experiment.
. 2. How many outcomes are in the sample space?
3. What is the probability that the letters chosen are AA?
Answers
1. The outcomes in the sample space of choosing a letter from the word STARK are: S, T, A, R, K.
2. Number of outcomes in the sample space = 6 (from THANKS) × 5 (from STARK) = 30.
3. The Probability of choosing the letters AA is 0, as there are no occurrences of the letter A in both words together.
1. The outcomes in the sample space of choosing a letter from the word THANKS are: T, H, A, N, K, S.
The outcomes in the sample space of choosing a letter from the word STARK are: S, T, A, R, K.
2. To find the number of outcomes in the sample space, we multiply the number of outcomes for each word.
Number of outcomes in the sample space = Number of outcomes for the first word × Number of outcomes for the second word
Number of outcomes in the sample space = 6 (from THANKS) × 5 (from STARK) = 30.
3. The probability of choosing the letters AA would be the number of favorable outcomes (which is 0 in this case) divided by the total number of outcomes in the sample space.
Probability of choosing AA = Number of favorable outcomes / Total number of outcomes
Probability of choosing AA = 0 / 30 = 0.
Therefore, the probability of choosing the letters AA is 0, as there are no occurrences of the letter A in both words together.
To know more about Probability .
https://brainly.com/question/13604758
#SPJ11
on a standardized exam, the scores are normally distributed with a mean of 750 and a standard deviation of 25. find the z-score of a person who scored 775 on the exam.
Answers
To find the z-score of a person who scored 775 on the exam, we can use the formula:
z = (x - μ) / σ
where x is the individual's score, μ is the mean, and σ is the standard deviation.
In this case, the individual's score is 775, the mean is 750, and the standard deviation is 25. Plugging these values into the formula, we get:
z = (775 - 750) / 25 = 1
Therefore, the z-score of a person who scored 775 on the exam is 1.
A z-score represents the number of standard deviations an individual's score is away from the mean. It is a measure of how a given value relates to the average value of a set of data, taking into account the variability of the data.
By calculating the z-score, you can determine whether a data point is relatively high or low compared to the rest of the data set. A positive z-score indicates that the data point is above the mean, while a negative z-score indicates that it is below the mean.
In this case, a z-score of 1 indicates that the person's score is 1 standard deviation above the mean.
Learn more about z-scores here:
https://brainly.com/question/30557336
#SPJ11
Let f be the function defined by
f(x) = 3^x. If three subintervals of equal
length are used, what is the value of the left Riemann sum approximation for
3.5
2
3 dx? Round to the nearest
thousandth if necessary.
Answers
The left Riemann sum approximation is 14.892
How to determine the left Riemann sum approximationFrom the question, we have the following parameters that can be used in our computation:
f(x) = 3^x
The left Riemann sum can be expressed as:
\(R_n = h \sum_{i=1}^{n} \frac{4}{a + ih}\)
Such that:
h = (b - a)/n
In this case, a = 2, b = 3.5, n = 3, and f(x) = 3^x
So, the left Riemann sum approximation is:
Approximation = (3.5-2)/3 * (f(2 + 1/3 * (3.5-2)) + f(2 + 2/3 * (3.5-2)) + f(2 + 3/3 * (3.5-2)))
Approximation = 0.5/3 * (3^(2 + 1/3 * (3.5-2)) + 3^(2 + 2/3 * (3.5-2)) + 3^(2 + 3/3 * (3.5-2)))
Approximation = 14.892
Read more about derivative at
https://brainly.com/question/5313449
#SPJ1
determine if the numerical value describes a population parameter or a sample statistic. the average price of a house in the new subdivision is $257,000.
Answers
The numerical value in this sentence, "the average price of a house in the new subdivision is $257,000" describes a Population Parameter.
What is a Population Parameter?A population parameter is a figure that describes a fact about a whole population. In this sentence, we can see that the figure quoted is representative of an entire population. A sample statistic, on the other hand, describes something about a part of a population.
So, for the statement above, we can see that the average price is representative of all the houses in the new subdivision. Thus, the figure is a population parameter.
Learn more about population parameters here:
https://brainly.com/question/2292917
#SPJ4
A square garden has an area of 5 square feet. Without using a calculator, find the side length of the garden to the nearest tenth of a foot
Answers
Answer:
2.23
Step-by-step explanation:
tune able to find the area you should x one side by the other side to find the area 2.23 * 2.23 equals close to 5 square feet
consider the set of integers from 1 to 20 inclusive. this set has how many 3-element subsets, such that no two consecutive integers are in the subset?
Answers
It has 816 ways to 3-element subsets, such that no two consecutive integers are in the subset.
You need three digits from 1 to 20, but you don't want any consecutive ones. You should call them a, b, and c.
Without loss of generality, a < b < c.
We use combinations,
Remember that we can write a + 1 b if a b and they're not sequential. With the aid of this insight, we can see the number of desired the number of methods for choosing a, b, and c from among the integers so that,
(1 ≤ a) & (a + 1 < b) & (b + 1 < c) & (c ≤ 20)
In other words, you want to know how many possibilities there are to choose the three numbers a, b, and c so that;
1 ≤ a < b − 1 < c − 2 ≤ 18
As a result, the question is equal to asking how many ways there are to select three integers (a, b - 1, and c - 2) from a range of 1 to 18. In other words, we are interested in how many ways we can select three items from a total of 18 options.
So, the response is:
\((^1^8_3)\) = 816 ways
To learn more about combinations click here:
brainly.com/question/28042664
#SPJ4