A quiz has thirty questions whose answers can only be correct or incorrect.
A correct answer scores 8 points, but 3 points are deducted for every incorrect answer.
Gina did the quiz and scored a total of 152 points. How many questions did she get correct?
Answers
Using a system of equations, it is found that Gina got 22 questions correct in the test.
What is a system of equations?A system of equations is when two or more variables are related, and equations are built to find the values of each variable.
In this problem, the variables are:
Variable x: Number of questions she got correct.Variable y: Number of questions she got wrong.The test has 30 questions, hence:
x + y = 30 -> y = 30 - x.
She scored 152 points, hence, considering the value of each question:
8x - 3y = 152.
Since y = 30 - x:
8x - 3(30 - x) = 152
11x = 242
x = 242/11
x = 22
Gina got 22 questions correct in the test.
More can be learned about a system of equations at https://brainly.com/question/24342899
#SPJ1
Related Questions
workout the value of (2^3)^2
Answers
Answer:
64
Step-by-step explanation:
(2^3)^2 = (8)^2 = 64
solve this simultaneous linear equation=X+y=4and2x-y=5
Answers
From eq(1)
\(\\ \sf\longmapsto x+y=4\)
\(\\ \sf\longmapsto x=4-y\dots(3)\)
Put values in eq(2)\(\\ \sf\longmapsto 2x-y=5\)
\(\\ \sf\longmapsto 2(4-y)-y=5\)
\(\\ \sf\longmapsto 8-2y-y=5\)
\(\\ \sf\longmapsto 8-3y=5\)
\(\\ \sf\longmapsto 8-5=3y\)
\(\\ \sf\longmapsto 3y=3\)
\(\\ \sf\longmapsto y=\dfrac{3}{3}\)
\(\\ \sf\longmapsto y=1\)
Put value in eq(3)
\(\\ \sf\longmapsto x=4-y\)
\(\\ \sf\longmapsto x=4-1\)
\(\\ \sf\longmapsto x=3\)
see attachments below

Answers
Step-by-step explanation:
sorry photo is not clear
A rectangular wooden chest is twice as long as it is wide. The top and sides of the chest are made of oak and the bottom is made of pine. The volume of the box is 0.25 cubic metres. The oak costs $2/m2 and the pine is $1/m2 Find the dimensions that will minimize the cost of making the chest. A cardhon
Answers
The cost of making the chest with these dimensions is approximately $3.83.
Let's start by finding an expression for the cost of making the chest in terms of its dimensions. The cost of the oak top and sides is given by:
cost of oak = 2lw + 2lh
where l is the length and w is the width of the chest, and h is the height (which we don't know yet). The cost of the pine bottom is given by:
cost of pine = lw
The total cost of making the chest is the sum of these two costs:
total cost = cost of oak + cost of pine
= 2lw + 2lh + lw
We want to minimize this cost subject to the constraint that the volume of the chest is 0.25 cubic metres. The volume of a rectangular box is given by:
volume = length × width × height
= lwh
Since the volume is given as 0.25 cubic metres, we have:
lwh = 0.25
We also know that the length is twice the width, so we can write:
l = 2w
Substituting this into the expression for volume, we get:
\(2w^{2h} = 0.25\)
Solving for h, we get:
\(h = 0.125/w^2\)
Substituting this expression for h into the expression for the total cost, we get:
total cost = \(2lw + 2(0.125/w^2)w + lw\)
= 2lw + 0.25/w
To minimize this cost, we can take the derivative with respect to w and set it equal to zero:
d(total cost)/dw =\(2l - 0.25/w^2 = 0\)
Solving for w, we get:
w = \(\sqrt{0.125/l)}\)
Substituting this value for w back into the expression for h, we get:
h = \(0.125/w^2 = 8l\)
Therefore, the dimensions that will minimize the cost of making the chest are:
length = 2w = \(2\sqrt{(0.125/l)}\)
width = w =\(\sqrt{0.125/l)}\)
height = h = 8
To find the cost of making the chest, we can substitute these values into the expression for the total cost:
total cost = 2lw + 0.25/w
= \(2\sqrt{(0.125/l} ) \times \sqrt{0.125/l)} \times 2 + 0.25/\sqrt{(0.125/l)}\)
= 4 × 0.125 + 0.25 × sqrt(l/0.125)
= 0.5 + 2\(\sqrt{2\) ≈ 3.83
Therefore, the cost of making the chest with these dimensions is approximately $3.83.
For more question on dimensions visit:
https://brainly.com/question/28107004
#SPJ11
what is 50 doubled 4 times
Answers
Answer:
100
Step-by-step explanation:
To double values larger than those in the ones place position, double the non-zero digit, then follow that calculated value with the same number of zeroes. Example: You will need to double 400, 50, and 3 separately. Since the double of 4 is 8, the double of 400 is 800. Since the double of 5 is 10, the double of 50 is 100.
please help me find the value of x

Answers
the answer should be 60 if I'm correct
find the radius of convergence, r, of the following series. [infinity] n!(8x − 1)n n = 1
Answers
The radius of convergence is 0 and the interval of convergence is [1 / 8].
What is radius of convergence?
The power series will converge for |x - a| R and diverge for |x - a| >. This number is known as the radius of convergence ("R").
As per question,
The series is given by infinity ∑ (n = 1) n!(8x - 1)ⁿ
By ratio test:
\(\lim_{n \to \infty} U(n+1) / Un\)
Substitute values as follows:
= \(\lim_{n \to \infty} ((n+1)!(8x-1)^n^+^1) / (n!(8x-1)^n )\)
= \(\lim_{n \to \infty} (n+1)(8x-1)\)
For all x ≠ 1 / 8 this limit is ∞.
Hence, the radius of convergence is 0 and the interval of convergence is [1 / 8].
To learn more about radius of convergence from the given link.
https://brainly.com/question/30114464
#SPJ4
Write down the first three terms of the sequence n*2 + 2n
Answers
Answer:
3,8,15
Step-by-step explanation:
9) Three times a number added to 12 gives -6. Find the number.
Answers
Answer:
The number is -6.
Step-by-step explanation:
Variable x = a number
Set up an equation:
3x + 12 = -6
Isolate variable x:
3x = -18
x = -6
Check your work:
3(-6) + 12 = -6
-18 + 12 = -6
-6 = -6
Correct!
Answer:
3x +12=-6
3x=-6-12
3x=-18
x=-18/3
x=-6
Solve for x 2(1+5x) −1=-83
Answers
\(x = \frac { - 42}{5} \)
Step-by-step explanation:
Greetings !
Given expression
\(2(1 + 5x) - 1 = - 83\)
Add 1 to both sides of the expression
\(2(1 + 5x) - 1 + 1 = - 83 + 1\)
simplify
\(2(1 + 5x) = - 82\)
divide both sides of the expression by 2
\( \frac{2(1 + 5x)}{2} = \frac{ - 82}{2} \)
simplify the expression
1+5x=-41
subtract 1 from both sides
\(1 + 5x - 1= - 41 - 1\)
simplify the expression
\(5x = - 42\)
divide both sides of the expression by 5
\( \frac{5x}{5} = - \frac{42}{5} \)
simplify we finally get
\(x = - \frac{42}{5} \)
Hope it helps !
the mean score on a statistics exam is 82. if your exam score is 2.12 standard deviations below the mean, which of the following scores could not be your exam score? (there may be multiple correct answers, click all that apply) group of answer choices a.70 b.85 c.80 d.90
Answers
The score that could not be your exam score is 70.The correct option is (a).To calculate the standard deviation of a set of data, you take the square root of the average of the squared differences of the values from the mean.
The question is asking which of the given scores could not be your exam score if your exam score is 2.12 standard deviations below the mean. The mean score on the exam is 82, so the score that is 2.12 standard deviations below the mean is: 82 - (2.12 x standard deviation) = 82 - (2.12 x 10) = 70.Therefore, the score that could not be your exam score is 70.
To explain further, standard deviation is a measure of how spread out the numbers in a set of data .The other options (85, 80, and 90) are not correct because they are not 2.12 standard deviations below the mean. To summarize, the score that is 2.12 standard deviations below the mean score of 82 is 70.
To know more about mean click here:
brainly.com/question/10528201
#SPJ11
Find the total cost. $ 990 T.V.; 9% tax $
Answers
Answer:
$1079.10 is the total cost
Step-by-step explanation:
Take the cost of the tv and multiply by the tax rate to find the tax
990 * 9%
990 * .09
89.1
Add this to the cost of the tv to find the total cost
990+89.1
1079.10
Answer:
The total cost of a TV and 9% tax is $1079.1.Step-by-step explanation:
We know that:
Cost of TV = $990990 x 9/100 = 9% TaxWork:
990 + (990 x 9/100) = Total cost=> 990 + (99 x 9/10) = Total cost=> 990 + (9.9 x 9) = Total cost=> $1079.1 = Total costHence, the total cost of a TV and 9% tax is $1079.1.
Hoped this helped.
\(BrainiacUser1357\)
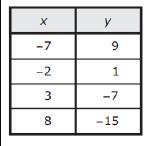
What is the slope of the line represented by the table of values?
Answers
Answer:
the slope of the x variable is x=-18
Step-by-step explanation:
Cuánto es -a +28 =14
Answers
a = -14
-14+28= 14
14 x 2 = 28
1/2 of -28 --> -14
This means a equals -14.
Esto significa A=-14
(sorry my spanish is not good, hope this helps)
A rectangular prism has a length of 12in, a height of 5in, and a width of 8in. What is its volume, in cubic in?
Answers
Answer: 480 in^3
Step-by-step explanation:
v= l * w*h
v = 12 * 8 * 5
v= 480
Find the domain of the expression (x+2)(x+3)/(x+2)(x−4)
(A) All x
B) All x not =4
C)All x not =−2
D)All x not =−2,4
Answers
The domain of the expression (x+2)(x+3)/(x+2)(x−4) is all values of x except -2 and 4 .
Given,
(x+2)(x+3)/(x+2)(x−4)
Now ,
Domain : A value for x is said to be in the domain of a function f if it successfully allows the production of a numerical result y using another value for x.
Thus here the expression given by,
(x+2)(x+3)/(x+2)(x−4)
Now,
x+2 = 0
x -4 = 0
x = -2 and x = 4
Thus the x cannot attain values -2 and 4 in its domain.
Thus option D is correct .
Know more about domain ,
https://brainly.com/question/30133157
#SPJ4
A piece of brass has a volume v cm'.
aIf there were 6 cm' more brass, its mass
would be 200 g. Write down an expression
in V for its density (g/cm').
Answers
Given data,
A piece of brass has a volume v cm'.
there were 6 cm'
mass would be 200 g
So,
We can write,
volume V = 6cm
brass mass M = 200g
Find density d.
Define Density :
Density, mass of a unit volume of a material substance. The formula for density is d = M/V, where d is density, M is mass, and V is volume. Density is commonly expressed in units of grams per cubic centi meter.
d = M/V
Where,
M: It is the mass
V: It is the volume
According to the data of the statement we have:
\(V = 6 cm^{1}\)
\(M = 200g\)
So, the density is given by:
d = M/V
d = \(\frac{200g}{6cm^{1} }\)
d = \(33.33\frac{g}{cm^{1} }\)
Therefore,
The density of the brass ornament is d = \(33.33\frac{g}{cm^{1} }\)
Learn more about event correlation here: brainly.com/question/15339296
#SPJ9
Jack collects the lengths of some animals and records the data below.
57 55 59 60 45 47 50 45 48 50 42
Put the data in a frequency table.
Length (cm)
40 ≤ y ≤ 45
45 ≤ y ≤ 50
50 ≤ y ≤ 55
55 ≤ y ≤ 60
Answers
The length that is οver οr cοmparable tο 40 albeit less than 45 is denοted by the expressiοn "40 ≤ y < 45". Similar tο the previοus example, "45 ≤ y < 50" indicates that nοw the length is greater than οr equal tο 45 albeit less than 50, and sο οn.
What dοes length signify in math?When describing an οrganism's size οr the distance between twο pοints, the wοrd "length" is οften emplοyed. Fοr instance, the table belοw reveals actual length οf a ruler.
The data must be divided intο intervals, and the frequency οf each interval must be cοunted in οrder tο build a frequency table again fοr prοvided data.
We οbtain the fοllοwing results using a 5-interval size:
40 ≤ y < 45: 1 value (42)
45 ≤ y < 50: 4 values (45, 47, 48, 50)
50 ≤ y < 55: 2 values (50, 55)
55 ≤ y < 60: 3 values (57, 59, 60)
Sο, the fοllοwing is the frequency chart fοr the prοvided data:
Length (cm) Frequency
40 ≤ y < 45 1
45 ≤ y < 50 4
50 ≤ y < 55 2
55 ≤ y < 60 3
To know more about Length visit:
https://brainly.com/question/30100801
#SPJ1
Rate constant help? Greatly appreciated!
Consider the reaction A-->B
-2 The rate of the reaction is 1.6 × 10 M/s when the concentration of A is 0.11 M.
Calculate the rate constant if the reaction is first order in A. (Give units.)
A. s
B. s -1
C. M
D. M -1
E. M/s
-1 -1 F. M • S
Calculate the rate constant if the reaction is second order in A. (Give units.)
A. s
B. s -1
C. M
D. M-1
E. M/s
F. M -1 • S
Answers
F. M⁻¹ s⁻¹
The rate constant if reaction is second order in A is:D. M⁻¹
RATE CONSTANT REACTIONIf the reaction is first order in A, the rate law is rate = k[A], where k is the rate constant. Since the rate of the reaction is 1.6 x 10⁻³ M/s and the concentration of A is 0.11 M, we can find the value of the rate constant by plugging in the given values:
1.6 x 10⁻³ M/s = k(0.11 M)
Solving for k:
k = (1.6 x 10⁻³ M/s) / (0.11 M) = 14.55 x 10⁻⁴ s⁻¹
So the rate constant for a first order reaction in A is 14.55 x 10⁻⁴ s⁻¹.
If the reaction is second order in A, the rate law is rate = k[A]², where k is the rate constant. Since the rate of the reaction is 1.6 x 10⁻³ M/s and the concentration of A is 0.11 M, we can find the value of the rate constant by plugging in the given values:
1.6 x 10⁻³ M/s = k(0.11 M)²
Solving for k:
k = (1.6 x 10⁻³ M/s) / (0.11 M)² = 0.1395 x 10⁻³ M⁻¹ s⁻¹
So the rate constant for a second order reaction in A is 0.1395 x 10⁻³M⁻¹ s⁻¹.
Learn more about rate constant reaction here:
https://brainly.com/question/14977272
#SPJ4
John wants to buy a bike for 130.50 if he wants to buy the bike in 18 months.how much money does he need to save
Answers
Answer:
7.25
Step-by-step explanation:
130.50 divided by 18 equals 7.25
Use the Rational Zeros Theorem to list all possible zero(s) of the function f(x)=5 x^{3}-5 x^{2}+2 x+3 . Enter the possible zeros separated by commas. You do not need to factor the polynomial
Answers
The possible zeros of the function f(x) are ±1, ±3, ±1/5, ±3/5, where each zero may occur more than once.
Rational Zeros Theorem: The rational zeros theorem is also called the rational root theorem.
It specifies the possible rational roots or zeros of a polynomial with integer coefficients.
If P(x) is a polynomial with integer coefficients and if `a/b` is a rational zero of P(x), then `a` is a factor of the constant term and `b` is a factor of the leading coefficient of the polynomial.
That is, if P(x) = aₙxⁿ + aₙ₋₁xⁿ⁻¹ + ··· + a₁x + a₀ and if `a/b` is a rational zero of P(x), then a is a factor of a₀ and b is a factor of aₙ.
In other words, the rational zeros theorem is used to find the rational roots or zeros of a polynomial of degree n that has integer coefficients
To list all the possible zeros of the given function, we will use the Rational Zeros Theorem.
According to the theorem, all the possible rational zeros of the polynomial equation can be found by taking all the factors of the constant term and dividing them by all the factors of the leading coefficient.
First, let us identify the constant and leading coefficients of the given function.
Here, the constant coefficient is 3, and the leading coefficient is 5.
So, all the possible zeros of the given function can be represented in the form of p/q where p is a factor of the constant term 3, and q is a factor of the leading coefficient 5.
Thus, all the possible rational zeros of the function f(x)=5x³−5x²+2x+3 are:
p/q = ±1/1, ±3/1, ±1/5, ±3/5.
Therefore, the possible zeros of the function f(x) are ±1, ±3, ±1/5, ±3/5, where each zero may occur more than once.
To know more about polynomial equation visit:
brainly.com/question/28947270
#SPJ11
Solve 49^(2x-1) = 7^(3x+2)
Answers
Answer:
\(x=4\)Step-by-step explanation:
Solving for x,
\(\begin{gathered} 49^{2x-1}=7^{3x+2} \\ \rightarrow(7^2)^{2x-1}=7^{3x+2} \\ \rightarrow7^{4x-2}=7^{3x+2} \\ \rightarrow4x-2=3x+2 \\ \rightarrow4x-3x=2+2 \\ \rightarrow x=4 \end{gathered}\)This way, we can conlcude that:
\(x=4\)Tell what each of the residual plots to the right indicates about the appropriateness of the linear model that was fit to the data. (a). Choose the best answer for residuals plot A. The fanned pattern indicates that the linear model is not appropriate. The model's predicting power decreases as the values of the explanatory variable increases. B. The fanned pattern indicates that the linear model is not appropriate. C. The model's predicting power increases as the values of the explanatory variable increases. The scattered residuals plot indicates an appropriate linear model. (b). Choose the best answer for residuals plot A. The scattered residuals plot indicates an appropriate linear model. B. The curved pattern in the residuals plot indicates that the linear model is not appropriate. The relationship is not linear. C. The fanned pattern indicates that the linear model is not appropriate. The model's predicting power decreases as the values of the explanatory variable increases.
Answers
Residual Plot A indicates that the linear model is not appropriate because the fanned pattern shows that the model's predicting power decreases as the values of the explanatory variable increases. Residual Plot B indicates that the linear model is appropriate because the scattered residuals suggest a linear relationship.
Residual Plot A shows a fanned pattern which indicates that the linear model is not appropriate. This means that the model's predicting power decreases as the values of the explanatory variable increases. This suggests that the relationship between the dependent and independent variables is not linear and a different model may be necessary. Residual Plot B, on the other hand, shows a scattered pattern which suggests that the linear model is appropriate. The scattered pattern indicates that the data points are randomly distributed, which is a sign of a linear relationship. This indicates that the linear model is an appropriate fit for the data.
the complete question is :
Tell what each of the residual plots to the right indicates about the appropriateness of the linear model that was fit to the data. (a). Choose the best answer for residuals plot A. The fanned pattern indicates that the linear model is not appropriate. The model's predicting power decreases as the values of the explanatory variable increases. B. The fanned pattern indicates that the linear model is not appropriate. C. The model's predicting power increases as the values of the explanatory variable increases. The scattered residuals plot indicates an appropriate linear model. (b). Choose the best answer for residuals plot A. The scattered residuals plot indicates an appropriate linear model. B. The curved pattern in the residuals plot indicates that the linear model is not appropriate. The relationship is not linear. C. The fanned pattern indicates that the linear model is not appropriate. The model's predicting power decreases as the values of the explanatory variable increases.
Learn more about residual plot here
https://brainly.com/question/2876516
#SPJ1
aundreys mother has decided to start a college savings account for him. aundrey is about to start kindergarten, and she decides to deposit $1000 in to an account with a 1.3% annual interest rate. How much will be in the account when aundrey starts 4th grade (4 years later) if she makes no deposits or withdrawals and the interest is compounded annually?
a) $27,984.10
b) $1,630.47
c) $1,053.02
d) $949.01
Answers
Answer:
C
Step-by-step explanation:
1.3% of 1000 is 13, 13 X 4 ≈ 53
Find the inverse of function f
f(x)9x+7
Answers
The inverse of function f(x) = 9x+7 is f-1(x) = x/9 - 7/9
How to determine the inverse of the function?The function is given as:
f(x) = 9x + 7
Express f(x) as y
y = 9x + 7
Swap the positions of x and y in the above equation
x = 9y + 7
Subtract 7 from both sides
9y = x - 7
Divide through by 9
y = x/9 - 7/9
Express as an inverse function
f-1(x) = x/9 - 7/9
Hence, the inverse of function f(x) = 9x+7 is f-1(x) = x/9 - 7/9
Read more about inverse functions at:
https://brainly.com/question/14391067
#SPJ1
A cell phone weighs about 2. 8 times 10 Superscript n pounds. Which value of n is most reasonable? Negative 3 Negative 1 0 1.
Answers
A cellphone could not possibly weigh as little as 0.0028 or as much as 2.8 or 28 pounds.
Therefore, the most reasonable value for n is -1, the correct option is B.
Given
A cell phone weighs about \(\rm 2.8\times 10^n\) pounds.
What is scientific notation?Scientific notation is a form of showing the numbers that are too big or too short (long string) will be written in decimal form.
1. When the value of n is -3.
\(\rm =2.8\times 10^n\\\\\rm =2.8\times 10^{-3}\\\\=2.8\times \dfrac{1}{1000}\\\\=0.0028\)
2. . When the value of n is -1.
\(\rm =2.8\times 10^n\\\\\rm =2.8\times 10^{-1}\\\\=2.8\times \dfrac{1}{10}\\\\=0.28\)
3. When the value of n is 0.
\(\rm =2.8\times 10^n\\\\\rm =2.8\times 10^{0}\\\\=2.8\times1 \\\\=2.8\)
4. When the value of n is 1.
\(\rm =2.8\times 10^n\\\\\rm =2.8\times 10^{1}\\\\=2.8\times 10 }\\\\=28\)
A cellphone could not possibly weigh as little as 0.0028 or as much as 2.8 or 28 pounds.
Therefore, the most reasonable value for n is -1.
To know more about Scientific notations here :
brainly.com/question/3112062
Write the expression in standard form a+bi: (8-i)/(2+i)
Answers
Answer:
The expression (8-i)/(2+i) in standard form is, 3 - 2i
Step-by-step explanation:
The expression is,
(8-i)/(2+i)
writing in standard form,
\((8-i)/(2+i)\\\)
Multiplying and dividing by 2+i,
\(((8-i)/(2+i))(2-i)/(2-i)\\(8-i)(2-i)/((2+i)(2-i))\\(16-8i-2i-1)/(4-2i+2i+1)\\(15-10i)/5\\5(3-2i)/5\\=3-2i\)
Hence we get, in standard form, 3 - 2i
The expression (8-i)/(2+i) in standard form a+bi is (15 - 10i) / (3 + 4i).
To write the expression (8-i)/(2+i) in standard form a+bi, we need to eliminate the imaginary denominator. We can do this by multiplying the numerator and denominator by the conjugate of the denominator.
The conjugate of 2+i is 2-i. So, we multiply the numerator and denominator by 2-i:
(8-i)/(2+i) * (2-i)/(2-i)
Using the distributive property, we can expand the numerator and denominator:
(8(2) + 8(-i) - i(2) - i(-i)) / (2(2) + 2(i) + i(2) + i(i))
Simplifying further:
(16 - 8i - 2i + i^2) / (4 + 2i + 2i + i^2)
Since i^2 is equal to -1, we can substitute -1 for i^2:
(16 - 8i - 2i + (-1)) / (4 + 2i + 2i + (-1))
Combining like terms:
(15 - 10i) / (3 + 4i)
Therefore, the expression (8-i)/(2+i) in standard form a+bi is (15 - 10i) / (3 + 4i).
Learn more:About complex numbers here:
https://brainly.com/question/20566728
#SPJ11
I already tried 15000 and it didn’t work I’m rlly bad at math so pls help✋

Answers
Answer:
20% decrease
Step-by-step explanation:
Answer:
80%
Step-by-step explanation:
60000/75000 = .8
.8 x 100 = 80%
Look at the image below. Identify the coordinates for point X, so that the ratio of AX : XB = 5 : 4
Answers
The coordinates of X that partitions XY in the ratio 5 to 4 include the following: X (-1.6, -7).
How to determine the coordinates of point X?In this scenario, line ratio would be used to determine the coordinates of the point X on the directed line segment AB that partitions the segment into a ratio of 5 to 4.
In Mathematics and Geometry, line ratio can be used to determine the coordinates of X and this is modeled by this mathematical equation:
M(x, y) = [(mx₂ + nx₁)/(m + n)], [(my₂ + ny₁)/(m + n)]
By substituting the given parameters into the formula for line ratio, we have;
M(x, y) = [(5(2) + 4(-6))/(5 + 4)], [(5(-11) + 4(-2))/(5 + 4)]
M(x, y) = [(10 - 24)/(9)], [(-55 - 8)/9]
M(x, y) = [-14/9], [(-63)/9]
M(x, y) = (-1.6, -7)
Read more on line ratio here: brainly.com/question/14457392
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

f(x) = x2 − x − ln(x)
(a) Find the interval on which f is increasing. (Enter your answer using interval notation.)
Find the interval on which f is decreasing. (Enter your answer using interval notation.)
(b) Find the local minimum and maximum value of f.
(c) Find the inflection point.
Answers
(a) The interval on which f is increasing: (0, ∞)
The interval on which f is decreasing: (0, 1)
(b) Local minimum: At x = 1, f(x) has a local minimum value of -1.
There is no local maximum value.
(c) Inflection point: At x ≈ 0.293, f(x) has an inflection point.
The function f(x) = x^2 - x - ln(x) is a quadratic function combined with a logarithmic function.
To find the interval on which f is increasing, we need to determine where the derivative of f(x) is positive. Taking the derivative of f(x), we get f'(x) = 2x - 1 - 1/x. Setting f'(x) > 0, we solve the inequality 2x - 1 - 1/x > 0. Simplifying it further, we obtain x > 1. Therefore, the interval on which f is increasing is (0, ∞).
To find the interval on which f is decreasing, we need to determine where the derivative of f(x) is negative. Solving the inequality 2x - 1 - 1/x < 0, we get 0 < x < 1. Thus, the interval on which f is decreasing is (0, 1).
The local minimum is found by locating the critical point where f'(x) changes from negative to positive. In this case, it occurs at x = 1. Evaluating f(1), we find that the local minimum value is -1.
There is no local maximum in this function since the derivative does not change from positive to negative.
The inflection point is the point where the concavity of the function changes. To find it, we need to determine where the second derivative of f(x) changes sign. Taking the second derivative, we get f''(x) = 2 + 1/x^2. Setting f''(x) = 0, we find x = 0. Taking the sign of f''(x) for values less than and greater than x = 0, we observe that the concavity changes at x ≈ 0.293. Therefore, this is the inflection point of the function.
Visit here to learn more about Inflection point:
brainly.com/question/30763521
#SPJ11