a quadrilateral that is not a rectangle is inscribed in a circle. what is the least number of arc measures needed to determine the measures of each antgle in the quadrialteral
Answers
The least number of arc measures needed to determine the measures of each angle in the inscribed quadrilateral is 2.
To determine the measures of each angle in the quadrilateral, we need to find the central angles of the arcs that intersect the quadrilateral's vertices. Since the quadrilateral is not a rectangle, it is not a cyclic quadrilateral, which means that its opposite angles do not add up to 180 degrees.
Therefore, we need to use the fact that the sum of the measures of the opposite angles in an inscribed quadrilateral is 360 degrees. Let the angles of the quadrilateral be A, B, C, and D, with opposite angles A and C, and B and D. We can find the measure of arc AC by drawing a chord connecting the endpoints of AC and finding the central angle that intercepts it. Similarly, we can find the measure of arc BD.
Now, we can use the fact that the sum of the central angles that intercept arcs AC and BD is equal to 360 degrees. Let these angles be x and y, respectively. Then, we have:
x + y = 360
We can solve for one of the variables, say y, in terms of the other:
y = 360 - x
Substituting this into the equation for arc BD, we have:
2x + 2(360 - x) = arc BD
Simplifying this equation, we get:
arc BD = 720 - 2x
Now, we can use the fact that the sum of the measures of angles A and C is equal to the measure of arc AC, and the sum of the measures of angles B and D is equal to the measure of arc BD. Therefore, we have:
A + C = arc AC
B + D = arc BD = 720 - 2x
We need to find the least number of arc measures needed to determine the measures of A, B, C, and D. Since we have two equations and two variables (x and A), we can solve for both variables. Then, we can use the equations for B and D to find their measures.
Solving for A in terms of x, we have:
A = arc AC - C
A = 360 - x - C
Substituting this into the equation for B + D, we have:
(360 - x - C) + B + D = 720 - 2x
Simplifying this equation, we get:
B + D = 360 + x - C
Now, we have three equations and three variables (x, A, and C). We can solve for each variable in terms of x, and then use the equation for B + D to find their measures.
Therefore, the least number of arc measures needed to determine the measures of each angle in the quadrilateral is two: arc AC and arc BD.
Learn more about quadrilateral here: brainly.com/question/29119487
#SPJ11
Related Questions
◄)) Divide:
4) 8,567
R
Submit
Answers
The Remainder is 3 and the Quotient is 2141.
What is meant by long term division?Long division is a mathematical technique for breaking down large numbers into smaller groups or parts. It is beneficial to divide a problem into simple and easy steps. Dividends, divisors, quotients, and remainders are all part of the long divisions.The layout of short division and long division is similar, but there are two major differences. Long division is used when dividing multi-digit numbers by two-digit numbers, whereas short division is used when dividing multi-digit numbers by one-digit numbers. Follow the steps below to find the square root of 5 using the long division method. As a result, the value of root 5 is 5 = 2.2360... Long division can be used to calculate the value of the square root of any non-perfect square number.Therefore,
The given Divisor = 4 and Dividend = 8567
4 ÷ 8567
= 2141.75
The Quotient is 2141 and the Remainder is 3
To learn more about long term division, refer to:
https://brainly.com/question/25289437
#SPJ1

please help will give brainliest

Answers
The correct explicit rule is f(n) = 50 + 30n
What is Explicit Rule?An explicit rule is a mathematical formula that directly gives the n-th term of a sequence or the value of a function for a given input, without the need to find other terms first. It can be expressed using variables, constants, and operations such as addition, subtraction, multiplication, and division.
To determine who is correct, we need to first understand the meaning of the variables in the explicit rules.
Let n be the number of days the car is rented for.
Let f(n) be the cost of renting the car for n days.
The deposit is a one-time charge and is not dependent on the number of days rented. Therefore, the constant term in the explicit rule should be 50.
Now, for each day rented, the cost is $30. This means that the cost for n days should be 30n.
So the correct explicit rule is:
f(n) = 50 + 30n
Therefore, Kevin is correct with the explicit rule f(n) = 50 + 30(n-1). This is because we subtract 1 from n since the deposit is charged only once at the beginning and is not included in the daily rate.
Suzanne's explicit rule, f(n) = 80 + 30(n-1), adds an extra $30 to the cost of renting the car, which is not correct.
To learn more about Explicit Rule from the given link
https://brainly.com/question/12620593
#SPJ1
From a survey of 100 drivers, 37 said they drove cars, 43 said they drove trucks, 12 said they drove vans, and 8 said they drove motorcycles. Out of 5,000 drivers, predict how many will drive a car.
Answers
Out of 5,000 drivers, there 1,850 are person drive the car.
What is Proportional?
Any relationship that is always in the same ratio and quantity which vary directly with each other is called the proportional.
Given that;
From a survey of 100 drivers, 37 said they drove cars, 43 said they drove trucks, 12 said they drove vans, and 8 said they drove motorcycles.
Now,
Since, From a survey of 100 drivers, 37 said they drove cars.
Hence, Out of 5,000 drivers;
Let the number of person drive the car = x
So, By definition of proportion, we get;
⇒ 100 / 37 = 5000/x
Solve for x as;
⇒ x = 5000 × 37 / 100
⇒ x = 50 × 37
⇒ x = 1,850
Thus, The number of person drive the car = 1,850
Learn more about the proportion visit:
https://brainly.com/question/1496357
#SPJ2
(6x^2) (4x^2)
nd some help
Answers
Answer:
So, I solved it and I got this:
Simplify the expression.
24 x^ 4
Step-by-step explanation:
hope this helps! have a great day!
how do you do 16 * -4 by step by step
Answers
16 * -4 = -64
First, 16*4 = 64.
Second, a positive times a negative equals a negative.
Other justification:
16 x -4 means you add -4 to itself 16 times:
-4 + -4 + -4 + -4 + ... for a total of 16 times gives you -64.
Please help meeeeeee!!!!!!!!

Answers
Factor the polynomial function over the complex numbersf(x)=x^4+9x^3+15x^2+9x+14
Answers
The polynomial function over the complex numbers is,
(x + 1i) ( x - 1i) (x+ 7) ( x + 2).
What is factoring a polynomial?
Factorization of polynomials, also known as polynomial factorization, is a mathematical and computer algebraic technique that combines irreducible factors with coefficients in the same domain to produce a polynomial with coefficients in a given field or in integers.
Consider, the given polynomial
f(x) = x^4 + 9x^3 + 15x^2 + 9x + 14
We can use a factoring "trick" here....write this as
x^4 + 9x^3 + 14x^2 + x^2 + 9x + 14 = 0 factor by grouping
x^2 ( x^2 + 9x + 14) + 1 ( x^2 + 9x + 14) = 0
(x^2 + 1) (x^2 + 9x + 14) = 0
(x^2 + 1) (x^2 + 9x + 14) = 0
⇒ (x^2 + 1) = 0, (x^2 + 9x + 14) = 0
x^2 = -1, x^2 + 7x + 2x + 14 = 0
x = ±i , x(x + 7) + 2(x + 7) = 0
x = ±i , (x + 7)(x + 2) = 0
⇒ (x + i)(x - i)(x + 7)(x - 7) = 0
(x + 1i) ( x - 1i) (x+ 7) ( x + 2) = 0
Hence, the polynomial function over the complex numbers is,
(x + 1i) ( x - 1i) (x+ 7) ( x + 2).
To know more about factoring a polynomial, click on the link
https://brainly.com/question/24351176
#SPJ4
The total length of a road trip was 13.2 hours. If highway signs are posted every 0.06 hours, including one at the end of the road trip, how many highway signs will there be on the road trip?
Answers
There will be 221 highway signs on the road trip.
What is Total Length?
Whole Length (TL) is the measurement taken in a straight line, with the fish lying on its side, from the tip of the snout to the end of the tail (caudal fin).
The total length of the road trip is 13.2 hours.
Highway signs are posted every 0.06 hours. To find out how many highway signs are on the road trip, we can divide the total length of the road trip by the interval between each sign and then add one more sign for the end of the road trip:
(number of signs) = (total length of road trip) / (interval between signs) + 1
Substituting the values, we get:
(number of signs) = 13.2 / 0.06 + 1
(number of signs) = 220 + 1
(number of signs) = 221
Therefore, there will be 221 highway signs on the road trip.
To know more about Total Length visit,
https://brainly.com/question/26319327
#SPJ1
7) Find the perimeter of triangle ABC. Round all answers to the nearest tenth.[6 points)
A
Please help!!! I’ll mark brain list too!

Answers
Answer: 14.6
Step-by-step explanation:
I made a square around the triangle which I then counted the squares, found the Pythagorean theorem, and then added the missing sides together
What is x equal to? ;-;

Answers
Answer:
18 > x or x < 18
Step-by-step explanation:
This is a linear inequality.
15(x + 1) + 7 > 11x + 4 + 5x
15x + 22 > 16x + 4
22 - 4 > 16x - 15x
= 18 > x
The graph of the function g(x) is a transformation of the parent function f(x)=x^2.
Which equation describes the function g?
g(x)=x^2+3
g(x)=(x+3)^2
g(x)=(x−3)^2
g(x)=x^2−3

Answers
The fuction f(x) = x², as represented in the graph. we now need to fond the equation of function G(x) which is same as function f(x) but slightly displaced to the left side of x - axis.
As we know, when the displacement is along negative x - axis (let it be c), the function changes as :
\(\qquad\displaystyle \tt \dashrightarrow \: g(x) = f(x + c)\)
\(\qquad\displaystyle \tt \dashrightarrow \: g(x) = (x + c) {}^{2} \)
Now, lets check it out to fond the value of c ~
put value of x and y from any point on the graph of g(x)
[ let it be (-3, 0) ]
\(\qquad\displaystyle \tt \dashrightarrow \: 0 =( - 3 + c) {}^{2} \)
\(\qquad\displaystyle \tt \dashrightarrow \: 0 = ( - 3 + {c}^{} )\)
\(\qquad\displaystyle \tt \dashrightarrow \: c = 0 + 3\)
\(\qquad\displaystyle \tt \dashrightarrow \: c = 3\)
now, plug in the value of of c in the required equation and its done ~
\(\qquad\displaystyle \tt \dashrightarrow \: g(x) = (x + 3) {}^{2} \)
Please Help! 60 points for a rapid reply- please look at the question below= The Figure of circle A shown has a diameter of PR which intersects with QS at point B and the measurements shown, Calculate the following measures-


Answers
The measures in the circle given in the image above are calculated as:
1. m<PSQ = 130°; 2. m<AQS = 30°; 3. m(QR) = 100°; 4. m(PS) = 110°; 5. (RS) = 70°.
How to Find the Measures in the Circle?In order to find the measures in the circle shown, recall that according to the inscribed angle theorem, the measure of intercepted arc is equal to the central angle, but is twice the measure of the inscribed angle.
1. m<PSQ = m<PAQ
Substitute:
m<PSQ = 130°
2. Find m<PBQ:
m<PBQ = 1/2(m(PQ) + m(RS)) [based on the angles of intersecting chords theorem]
Substitute:
m<PBQ = 1/2(130 + 2(35))
m<PBQ = 100°
m<AQS = 180 - [m<BAQ + m<PBQ]
Substitute:
m<AQS = 180 - [(180 - 130) + 100]
m<AQS = 30°
3. m(QR) = m<QAR
Substitute:
m(QR) = 100°
4. m(PS) = 180 - m(RS)
Substitute:
m(PS) = 180 - 2(35)
m(PS) = 110°
5. m(RS) = 2(35)
m(RS) = 70°
Learn more about Measures in a Circle on:
https://brainly.com/question/27111486
#SPJ1
PLS HELP ILL GIVE 5 STARS AND BRAINLIEST TO THE 1ST CORRECT ANSWER


Answers
Answer:
9x^2 + 6x + 1
Step-by-step explanation:
area = side × side
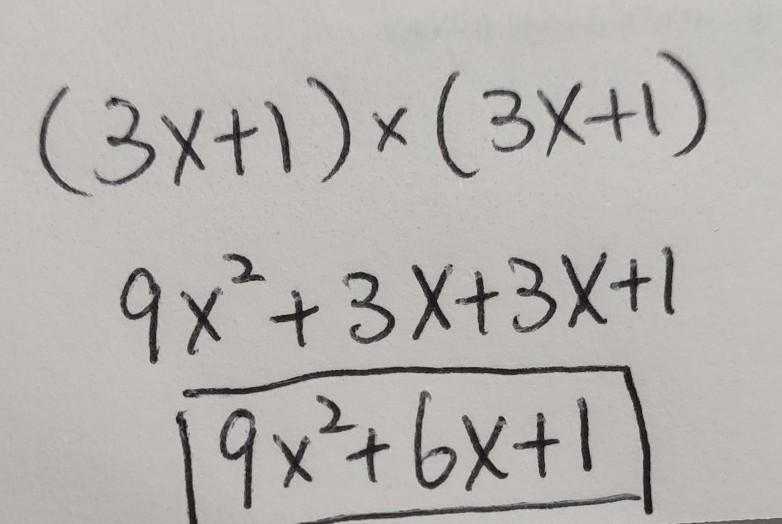
Lyndie is making reduced copies of a photo that measures 25 centimeters in height. She sets the copy machine to an 80% size reduction.
Part A
Write a percent equation that represents the relationship of the height of the first copy to the height of the original photo.
Part B
Lyndie wants to make another copy that will have a height of 17 cm. The copy machine settings increase or decrease in increments of 5%. Which photo should she make her copy from, the original or her first copy? Explain.
Answers
a) The enlargement needed to be done is 25%.
b) The succession time should be at least t=9 to get a final copy that is less than 15% of the original size.
What is Percentage?To determine the quantity or percentage of something in terms of 100, use the percentage formula. Per cent simply means one in a hundred. Using the percentage formula, a number between 0 and 1 can be expressed. A number that is expressed as a fraction of 100 is what it is. It is mostly used to compare and determine ratios and is represented by the symbol %.
Given:
Let the size of the page be q, when it is reduced to 80%, its size becomes
= 80% x q
= 0.80(q)
= 0.80q
When you want to return it into its original size q,
x(0.80q) = q
x = q / 0.80q
x = 1.25
x= 125%
Hence, the enlargement needed to be done is 25%.
b) The size of the page after t number of copying done is given by
C(t) = \(C_0(0.80)^t\)
So, C(t) / \(C_0\) = \((0.80)^t\)
0.15 ≤ \((0.80)^t\)
Taking log on both side
log (0.15) ≤ log \((0.80)^t\)
log (0.15) ≤ t log (0.80)
log (0.15) /log (0.80) ≤ t
0.80 ≤ t
Hence, the succession time should be at least t = 9 to get a final copy that is less than 15% of the original size.
Learn more about Percentage here:
https://brainly.com/question/29306119
#SPJ1
write an equation of the line in point slope form that passes through the given points (3,4) and (4,6)An equation of the line is??
Answers
re The point-slope form of a line is
\(y-y_1=m(x-x_1)\)The slope m of the line passing through these two points is the difference between their y coordinates divided by the difference between their x - coordinate.
\(m=\frac{6-4}{4-3}\)\(m=2\)Now we need only find the y-intercept.
Let us use the point (3, 4) which tells us that at x = 3, y = 4; therefore,
\(4-y_1=2(3)\)\(y_1=-2\)Hence, the question of our line in point-slope form is
\(\textcolor{#FF7968}{y+2=2x}\)Alternatively, when we have the slope of the line we would just use one of the points to quickly write the point-intercept form.
The y_1 and x_1 in the very first equation are the coordinates of one of the points on the line =. We know that one of the point on our line is (3, 4);
Mx-y when m=2,x=7. And y= 5
Answers
14-5= 9
So the answer is 9
Answer:
9
Step-by-step explanation:
mx - y (m = 2, x = 7, y = 5)
(2*7) - 5
= 14 - 5
= 9
If f(x) = 2x² +3 and g(x)=x2-7, find (f- g)(x)
A. 3x²2²-10
B. x² + 10
C. x²-4
D. 3x²2²-4
APEX FUNCTIONS PLEASE HELP
Answers
Answer: D
Step-by-step explanation:
Who can draw me an irregular pentagon (no sides or angles should be equal) and all the sides must be in inches and ONLY whole numbers. and all the angles of the irregular pentagon must equal to 540°.
Answers
An irregular pentagon with all sides in whole inches and angles summing up to 540 degrees can be drawn with the following measurements: 2 in, 3 in, 4 in, 5 in, and 8 in.
Explanation:
To draw an irregular pentagon with all sides in whole inches and angles summing up to 540 degrees, we need to use a combination of different side lengths that add up to 5 sides, while also ensuring that the angles add up to 540 degrees. One possible set of measurements for the sides of the pentagon that meet these requirements is:
2 inches
3 inches
4 inches
5 inches
8 inches
To confirm that the angles add up to 540 degrees, we can use the formula:
sum of interior angles = (n - 2) x 180
where n is the number of sides of the polygon. For a pentagon, n = 5, so the formula becomes:
sum of interior angles = (5 - 2) x 180 = 540 degrees
We can also check that the sides of the pentagon are unequal by comparing their lengths. As all the side lengths are whole numbers, we can easily verify that no two sides are the same. Therefore, we have successfully drawn an irregular pentagon with all sides in whole inches and angles summing up to 540 degrees, using the measurements of 2 in, 3 in, 4 in, 5 in, and 8 in.
To learn more about polygon click here, brainly.com/question/24464711
#SPJ11
find the expression 6u+6u–3u+5u
Answers
Answer:
14u
Step-by-step explanation:
6u+6u–3u+5u
= 12u - 3u + 5u
= 9u + 5u
= 14u
So, the answer is 14u
Amanda applied the associative property to (1 + 5) + 9 = 15. Which of the following might she have used?
A) 1 + 5 + 3(2 + 1) = 15
B) 1 + (5 + 9) = 15
C) 5 + 1 + 9 = 15
D) 9 + 1 + 5 =15
Answers
Answer:
D
I'm not sure but
The 9 has to be in in front of the brackets in order to tell us which operation we are using. If 1+5 is in brackets, then it would be D because y pi know what you are adding (1+5) to.
What is 7054.72 rounded to the nearest 10?
Answers
Answer:
7054.7
Step-by-step explanation:
7054.7 is 7054.72 rounded to the nearst 10
Answer:
7050
Step-by-step explanation:
7050, 5 is in tens and the 4 is in ones but it's less than 5 so it will be zero
Which number line represents the solutions to |x + 4| = 2?

Answers
Answer:
x=-2, -6 > pick the first answer choice !!!!!
Step-by-step explanation:
Let's solve your equation step-by-step.
|x+4|=2
Solve Absolute Value.
|x+4|=2
We know either x+4=2or x+4=−2
x+4=2 (Possibility 1)
x+4−4=2−4 (Subtract 4 from both sides)
x=−2
x+4=−2 (Possibility 2)
x+4−4=−2−4 (Subtract 4 from both sides)
x=−6
Answer:
x=−2 or x=−6
Answered by the ONE & ONLY #QUEEN herself aka #DRIPPQUEENMO!!!
HOPE THIS HELPED!!! BAHAHAHAHAHA
PLZZ HELPPP
Which matrix equation can be used to solve the system?
x+y=21
5x+4y=20

Answers
Answer:
\(X= \left[\begin{array}{ccc}-4&1\\5&-1\\\end{array}\right] \left[\begin{array}{ccc}21\\20\\\end{array}\right] \\\)
Step-by-step explanation:
Given the simultaneous equation
x+y=21
5x+4y=20
To write in matrix form, it must be in the form AX= b
X = A⁻¹b
A⁻¹ is the inverse of matrix A
A is a 2by2 matrix
X is the variables
b is a column matrix
The expression will therefore be written as;
\(A=\left[\begin{array}{ccc}1&1\\5&4\\\end{array}\right] \\\\|A| = 1(4)- 5(1)\\|A| = 4-5\\|A| = -1\\A^{-1} = -\left[\begin{array}{ccc}4&-1\\-5&1\\\end{array}\right] \\\\A^{-1} = \left[\begin{array}{ccc}-4&1\\5&-1\\\end{array}\right] \\\)
Hence the required product matrix that represent X is;
\(X= \left[\begin{array}{ccc}-4&1\\5&-1\\\end{array}\right] \left[\begin{array}{ccc}21\\20\\\end{array}\right] \\\)
(7x7x7x7x7x7x7)-3x-3x-3
Answers
Answer:
823516
Step-by-step explanation:
hope this helps
Answer:
7^7 times -3^3, or -22235661
Step-by-step explanation:
what is the smallest positive integer a such that the intermediate value theorem guarantees a zero exists between 0 and a?
Answers
The smallest positive integer that the intermediate value theorem guarantees a zero exists between 0 and a is 3.
What is the intermediate value theorem?
Intermediate value theorem is theorem about all possible y-value in between two known y-value.
x-intercepts
-x^2 + x + 2 = 0
x^2 - x - 2 = 0
(x + 1)(x - 2) = 0
x = -1, x = 2
y intercepts
f(0) = -x^2 + x + 2
f(0) = -0^2 + 0 + 2
f(0) = 2
(Graph attached)
From the graph we know the smallest positive integer value that the intermediate value theorem guarantees a zero exists between 0 and a is 3
For proof, the zero exists when x = 2 and f(3) = -4 < 0 and f(0) = 2 > 0.
Your question is not complete, but most probably your full questions was
Given the polynomial f(x)=− x 2 +x+2 , what is the smallest positive integer a such that the Intermediate Value Theorem guarantees a zero exists between 0 and a ?
Thus, the smallest positive integer that the intermediate value theorem guarantees a zero exists between 0 and a is 3.
Learn more about intermediate value theorem here:
brainly.com/question/28048895
#SPJ4

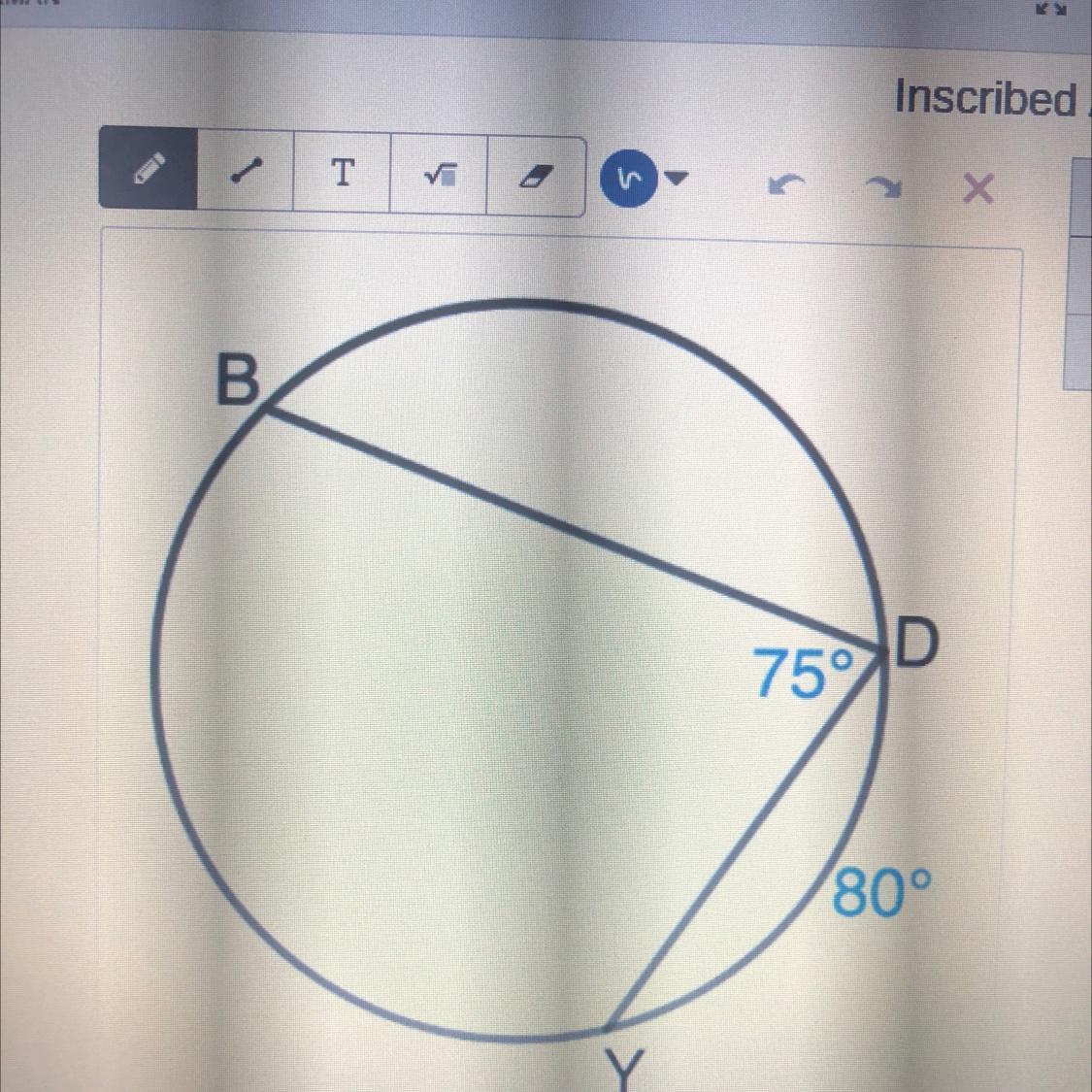
What is arc bd in this picture
Answers
a + b =c a + b + c = 36 given that a and b have the same value what is a,b and c
Answers
Answer:
a = 9 b = 9 c = 18
Step-by-step explanation:
a+b = c
a+ b + c = 36 but we know a+b = c sub that in
c + c = 36
c = 18 now a + b = c and a and b are the same
so a and b are = 9
Answer:
a is 9
b is 9
c is 18
Step-by-step explanation:
Let's list the information provided
a + b =c
a + b + c = 36
a=b
Knowing that a=b we can replace b with a in the equations
a+a is the same as 2a since a is being doubled
2a=c
Knowing this we can replace c with 2a
2a+2a=36
Now solve for a
\(2a+2a=36\\4a=36\\\frac{4a}{4} =\frac{36}{4} \\a=9\)
Now let's sub this value of a into the equations to see what the other values are
a=b
9=b
2a=c
2(9)=c
18=c
Suppose that scores on a recent statistics exam were normally distributed, that students in the 80th percentile of scores earned 85 points, and that students in the 30th percentile of scores earned 65 points. What was the mean of all exam scores in the class?.
Answers
The mean of all exam scores in the class is 72.67 ~ 73 . Mean is ratio of sum of score in all exam to the total numbers of all exams.
The exam scores are normally distributed , normally distributed is an arrangement in which most of values in middle and rest are symmetrically distributed at the ends 80th percentile of scores earned 85 it implies that 80% of students score is 85 or less and 30th percentile of scores earned 65 means 30% of students score is 65 or less .
Z-score value for 80th percentile is 0.841
Z-score value for 30th percentile is – 0.524
Formula for normally distributed,
Z =( X – μ) / σ
where μ is mean of scores , σ is standard deviations of scores ,X is sample mean
For 80th percentile , X= 85 , Z= 0.841
0.841=( 85- μ) /σ ----(1)
-0.524= (65-μ) / σ ----(2)
Solving equations (1) and (2)
- (841/524)= (85-μ )/( 65-μ) => 841μ – 841(65) = -524μ +85(524)
⇒ 1365μ= 99,205 => μ= 72.67
So, the value of mean of scores obtained by students in a class is 72.67 ~ 73
To learn more about normal distribution, refer:
https://brainly.com/question/27241794
#SPJ4
Sally has 42 cookies she wants to eat some and share some with her class if she hopes to share at least 35 with them with her class how many cookies can she eat?
Answers
Answer:
7 cookies
Step-by-step explanation:
42 - 35 = 7
Let A be a complex (or real) n x n matrix, and let x in C^n be an eigenvector corresponding to an eigenvalue (lambda) in C Show that for each nonzero complex scalar (nu) , the vector (nu) x is an eigenvector of A
Answers
The vector (nu) x is an eigenvector of A and corresponds to each nonzero complex scalar (nu) (lambda).
Let x in Cn be an eigenvector of A that corresponds to an eigenvalue. Assume that A is a n x n matrix (lambda). Ax = (lambda)x follows.
Let (nu) now be a complex scalar that is nonzero. A((nu)x) = A((nu)x) = A((nu)x) = A((nu)x) = A((nu)x) = A((nu)x)
As a result, (nu)x is an eigenvector of A that corresponds to (nu) (lambda).
Learn more about eigen vector here
https://brainly.com/question/13050052
#SPJ4