A point represents a location.
True
False
Answers
Related Questions
HELPPP!! PLEASE!!!!!

Answers
Answer:
y=15x
Step-by-step explanation:
Divide the change in y components of two points by the change in x components of a the points
60-30/4-2
30/2
=15
x=1
y=15
Equation: y=15x
I hope this helps :)
(someone please let me know if I'm incorrect and submit the correct answer)
I really need help on this

Answers
Answer:
Part A: \(\frac{3}{5}\)
Part B: \(\frac{1}{2}\)
Step-by-step explanation:
Pre-SolvingWe know that Alinn flipped a coin 20 times, and that 12 of those times resulted in heads. The other 8 times resulted in tails.
Part A wants us to find the experimental probability of the coin landing on heads. Experimental probability is the probability determined based on the experiments performed.
Part B wants us to find the theoretical probability of the coin landing on heads. Theoretical probability is determined based on the number of favorable outcomes over the number of possible outcomes.
Part A
Experimental probability is determined as # of times something occurred experimentally / total number of times.
Since 12 of the 20 times that Alinn flipped the coin resulted in heads, this means that the experimental probability of Alinn flipping heads is \(\frac{12}{20}\), which simplifies down to \(\frac{3}{5}\).
Part BTheoretical probability, as stated above, is the number of favorable outcomes / possible outcomes.
Our favorable outcome is flipping heads, and on a coin, there are two sides that a coin can land on: heads and tails. This means that there are two possible outcomes, and only one of them is favorable.
This means that our theoretical probability is \(\frac{1}{2}\).
due last month!!!!!!!!!

Answers
The required coordinates of C' after rotating triangle ABC 90° clockwise about the origin are (4, -5).
To rotate a point in the Cartesian plane 90° clockwise about the origin, we can use the following transformation:
(x', y') = (y, -x)
where (x, y) are the original coordinates and (x', y') are the new coordinates after rotation.
To find the coordinates of C' after rotating triangle ABC 90° clockwise about the origin, we can apply this transformation to point C(5, 4):
(x', y') = (y, -x)
(x', y') = (4, -5)
Therefore, the coordinates of C' after rotating triangle ABC 90° clockwise about the origin are (4, -5).
Learn more about transformation here:
https://brainly.com/question/11709244
#SPJ1
EXPRESS THE TRIG RATIOS AS FRACTIONS IN SIMPLEST TERMS (50 POINTS)
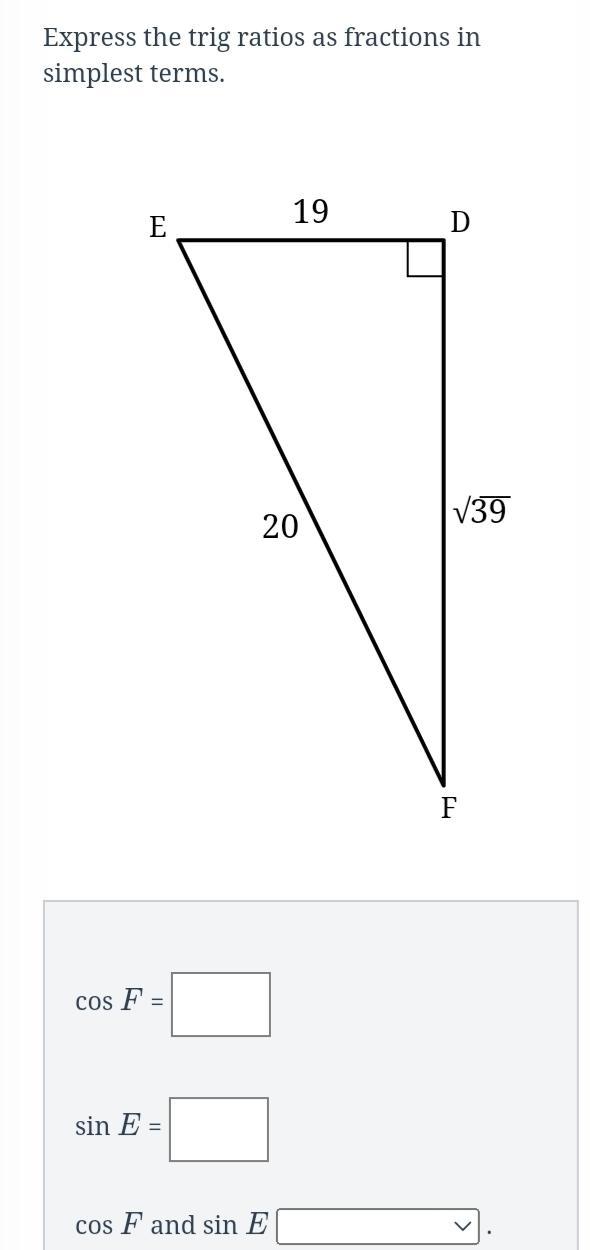
Answers
The value of cos F and sin E are equal to one another or they are equal angles since they have the same ratios
Trigonometric RatioTo solve this problem, we have to use the respective trigonometric ratio required.
Using SOHCAHTOA, we can use this to solve for all the unknown.
cos F
To solve for cos F, we can use the cosine value of F
\(cos F = \frac{adjacent}{hypothenuse} \\cos F = \frac{\sqrt{39} }{20}\)
Sin E
To solve for sin E, we can use the Sine value of E
\(sin E = \frac{opposite}{hypothenuse} \\sin E = \frac{\sqrt{39} }{20}\)
The value of cos F and sin E are the same.
Learn more on trigonometric ratio here;
https://brainly.com/question/24349828
#SPJ1
Find the following products :-
( -7 x² ) × 2 y
please give answer immediately
and give it correct
please don't write incorrect answer
Answers
Answer:
- 14x²y
Step-by-step explanation:
Given
- 7x² × 2y
= - 7 × 2 × x² × y
= - 14x²y
X^2 x y = x^2y
Therefore (-7x^2) x 2y = 14x^2y
6 Evaluate without using calculators. -4(-2)+(-12)÷(+3)+-20+(+4)+(-6
Answers
Answer:
Its 12
Step-by-step explanation:
1. Following PEMDAS, we first solve the equation inside the parentheses.
-4(-2) = 8
-12 ÷ 3 = -4
-20 + 4 = -16
2. Now, we have the following expression:
8 + (-4) + (-16)
3. Again, following PEMDAS, we solve the equation inside the parentheses first.
8 + (-4) + (-16) = 8 - 4 - 16
4. Finally, we solve the equation from left to right.
8 - 4 - 16 = 8 - (4 + 16)
8 - (20) = -12
Therefore, the value of the expression is -12.
Which statements are true about the graph of –6. 5 < x? Check all that apply. There is an open circle on –6. 5. There is an open circle on 6. 5. There is a closed circle on –6. 5. The graph includes the point 6. 5. The arrow points to the left. The arrow points to the right.
Answers
There is an open circle on –6. 5 and the arrow points to the right. The correct options are A and E.
What is inequality?Inequality is simply a type of equation that does not have an equal sign in it. Inequality is defined as a statement about the relative size as we will as is used to compare two statements.
The given expression is \(\rm x > -6.5\).
It means the value of x is more than -6.5.
Since the sign of equality is not there in the equation then at -6.5 will be an open circle. And the arrow points to the right.
The graph is shown below.
More about the inequality link is given below.
https://brainly.com/question/19491153

repeatedly rolling a die until getting a 3. you can express each individual outcome as a list. use ellipsis (...) as needed.
Answers
The correct answer is: To express each individual outcome when repeatedly rolling a die until getting a 3, you can create a list using the numbers rolled and an ellipsis (...) to indicate repetition.
To express each individual outcome when repeatedly rolling a die until getting a 3, you can create a list using the numbers rolled and an ellipsis (...) to indicate repetition. Your answer would be:
Individual outcome: {1, 2, 4, 5, 6, 3}, {1, 2, 4, 5, 6, 1, 2, 4, 5, 6, 3}, {1, 2, 4, 5, 6, 1, 2, 4, 5, 6, 1, 2, 4, 5, 6, 3}, ...
In each list, you roll the die until you get a 3, and you can repeat this process infinitely. The ellipsis indicates that this pattern continues indefinitely.
Learn more about individual outcome:
https://brainly.com/question/31388324
#SPJ11
A manufacturer of radial tires for automobiles has extensive data to support the fact that the lifetime of their tires follows a normal
distribution with a mean of 42,100 miles and a standard deviation of 2,510 miles. Identify the lifetime of a radial tire that corresponds to
the first percentile. Round your answer to the nearest 10 miles.
O47,950 miles
O 36,250 miles
47,250 miles
O 37,150 miles
O None of the above
Answers
the lifetime of a radial tire that corresponds to the first percentile 36,250 miles
To identify the lifetime of a radial tire that corresponds to the first percentile, we need to find the value at which only 1% of the tires have a lower lifetime.
In a normal distribution, the first percentile corresponds to a z-score of approximately -2.33. We can use the z-score formula to find the corresponding value in terms of miles:
z = (X - μ) / σ
Where:
z = z-score
X = lifetime of the tire
μ = mean lifetime of the tires
σ = standard deviation of the lifetime of the tires
Rearranging the formula to solve for X, we have:
X = z * σ + μ
X = -2.33 * 2,510 + 42,100
X ≈ 36,250
Rounded to the nearest 10 miles, the lifetime of the tire that corresponds to the first percentile is 36,250 miles.
To know more about deviation visit:
brainly.com/question/31835352
#SPJ11
Can someone please help me with this question

Answers
Answer
180 - x
Step-by-step explanation:
opposite angles of a quadrilateral inscribed in a circle are supplementary
Answer:
180-x !!!
Step-by-step explanation:
i had some time to think about it
In the year 2010 the population of sunshine city was 7,500 in the year 2020 the population of sunshine city was 8,000 if this trend continues what will be the population of sunshine city in the year 2025
Answers
Answer:
Ok so for every 10 years the population grows by 500 people so by 2025 it would have grown 250 people so 8250 people
hello please help i’ll give brainliest

Answers
Answer:
Volcanic Eruptions, Earthquakes, Erosion
I am very sorry if this is wrong
Have a great rest of your day and good luck!
Answer:
the answer is a, b, and d
Step-by-step explanation:
erosion is caused by wearing down overtime
Intersection find the extreme values of the function ƒ(x, y, z) = xy z2 on the circle in which the plane y - x = 0 intersects the sphere x2 y2 z2 = 4
Answers
There are no extreme values of the function ƒ(x, y, z) = xy z^2 on the given intersection.
To find the extreme values of the function ƒ(x, y, z) = xy z^2 on the given intersection, we need to find the critical points.
First, let's substitute y = x into the equation of the sphere:
x^2 (x^2) z^2 = 4
Simplifying the equation, we have:
x^4 z^2 = 4
Taking the square root of both sides, we get:
x^2 z = ±2
Now, we can substitute y = x into the equation of the function:
ƒ(x, y, z) = x(x)(z^2) = x^2 z^2
Since we have x^2 z^2 in both the function and the equation of the sphere, we can substitute x^2 z^2 = 4:
ƒ(x, y, z) = 4
The function ƒ(x, y, z) = 4 is a constant function, which means it has no critical points.
Know more about function here:
https://brainly.com/question/30721594
#SPJ11
Simplify
-6 + { 14 + { 60 - 9 ( 1 + 3 ) [}
Answers
-6 + [14 + (60-36)]
-6 + (14+24)
-6 + 38
32
whats bigger 1.11 or 1.101?
Answers
Answer:
1.11 is bigger
Step-by-step explanation:
how would you solve for v :
1/u + 1/v = 1/f

Answers
Step-by-step explanation:
\( \frac{1}{u} + \frac{1}{v} = \frac{1}{f} \)
\( \frac{1}{v} = \frac{1}{f} - \frac{1}{u} \)
\( \frac{1}{v} = \frac{u - f}{uf} \)
\(v = \frac{uf}{u - f} \)
the students of 3 sections of a class have to stand in rows each row has an equal number of students if there are 24 , 36 , and 60 students in 3 sections find the maximum number of students in each row
Answers
The maximum Number of scholars in each row is 12. This means that the scholars can be arranged in rows with an equal number of scholars, and each row can have a outside of 12 scholars.
To find the maximum number of scholars in each row, we need to determine the topmost common divisor( GCD) of the total number of scholars in each section. The GCD represents the largest number that divides all the given figures unevenly.
Given that there are 24, 36, and 60 scholars in the three sections, we can calculate the GCD as follows Step 1 List the high factors of each number 24 = 23 * 31 36 = 22 * 32 60 = 22 * 31 * 51
Step 2 Identify the common high factors among the three figures Common high factors 22 * 31 Step 3 Multiply the common high factors to find the GCD GCD = 22 * 31 = 4 * 3 = 12
thus, the maximum number of scholars in each row is 12. This means that the scholars can be arranged in rows with an equal number of scholars, and each row can have a outside of 12 scholars.
For more questions on Number .
https://brainly.com/question/26460978
#SPJ8
convert 500 minutes to hours
Answers
Answer:
8.33
Step-by-step explanation:
1hr=60 minutes
?hr = 500 minutes
To find how many hours, divide 500 by 60
500/60 = 8.33
500 minutes = 8.33 hours
What is the product of (−4)⋅(−4)⋅(−4)⋅y⋅y using exponents
Answers
Answer:
\((-4)^{3\)*\(y^{2}\)
This should be right.
If a translation is described as (x -5, y), how has the original image changed?
Answers
Answer:
It moves the x value 5 units to the left.
Step-by-step explanation:
"x - 5" means that we are subtracting 5 to whatever x value we are given. The "y" value doesn't change.
Since we are subtracting to the x value, we are going to move left 5 units.
Let's say we had the point (5, 5).
If we use the translation rule;
(5 - 5, 5)
(0, 5)
We moved the x value 5 units to the left.
Best of Luck!
Convert the point from rectangular coordinates to cylindrical coordinates. (6, 2√3, -9) (r, θ, z) = ( )
Answers
The cylindrical coordinates are (r, θ, z) = (6√2, 20°, -9).
The given rectangular coordinates are (6, 2√3, -9)
To convert to cylindrical coordinates (r, θ, z), we must find r, θ, and z.
r = √(6^2 + (2√3)^2)
r = √(36 + 12)
r = √48
r = 6√2
Now,
tanθ = 2√3/6
θ = tan^-1(2√3/6)
θ = tan^-1(1/3)
θ = 20°
z: z = -9
Therefore, the cylindrical coordinates are (r, θ, z) = (6√2, 20°, -9).
Learn more about the cylindrical coordinates here:
https://brainly.com/question/31046653.
#SPJ4
Which choice is an irrational number?

Answers
Answer: I think it's either 2 or 3 bc it's not number 4 and it's not number 1 for sure either one of those two
Step-by-step explanation:
Answer:
3
Step-by-step explanation:
sqrt of 18 is irrational because you cannot put it in ratio notation
the builder decided to survey the employees according to their trade. a random sample was selected from each trade.
Answers
The builder conducted a survey of employees based on their trades by selecting a random sample from each trade.
In order to gather information about the employees and their specific trades, the builder decided to conduct a survey. To ensure the survey results are representative of the entire employee population, the builder employed a random sampling method. This means that a sample group was selected from each trade, chosen in a way that gives every employee an equal chance of being included in the survey.
Random sampling is a widely used technique in survey research as it helps minimize bias and ensures the sample represents the larger population. By selecting a random sample from each trade, the builder can obtain a diverse range of perspectives and experiences across different trades within the company. This approach allows for a comprehensive understanding of the employees' opinions, needs, and concerns specific to their respective trades.
By conducting a survey based on trades and using random sampling, the builder can gain valuable insights into the workforce's specific dynamics, identify any common issues or areas for improvement, and make informed decisions regarding training, resource allocation, or policy changes to better support each trade within the organization.
Learn more about: Survey
brainly.com/question/31624121
#SPJ11
PLEASE HELP WITH MY MATH HOMEWORK
ill give brainliest

Answers
Answer:
The answer is that the ball was in the air for 0.56 seconds when it was 54 feet above the ground. This was determined by using the Quadratic Formula to solve the equation 54 = -16s^2 + 96s for the variable s.
Step-by-step explanation:
To solve this equation, we can use the Quadratic Formula, which states that for a quadratic equation in the form ax^2 + bx + c = 0, the solutions are given by:
x = (-b +/- sqrt(b^2 - 4ac)) / (2a)
In this case, a = -16, b = 96, and c = -54. Plugging these values into the Quadratic Formula, we get:
s = (-96 +/- sqrt(96^2 - 4 * -16 * -54)) / (2 * -16)
= (96 +/- sqrt(9216 + 4352)) / -32
= (96 +/- sqrt(13,568)) / -32
Since we want the time (in seconds) that the ball was in the air, we need to find the positive solution to this equation. Thus, we have:
s = (96 + sqrt(13,568)) / -32
= (96 + 120) / -32
= 0.5625 seconds
Rounding this value to the nearest hundredth of a second, we get 0.56 seconds. This means that the ball was in the air for 0.56 seconds when it was 54 feet above the ground.
To solve this equation, we used the Quadratic Formula. This method allowed us to find the time (in seconds) that the ball was in the air by solving for the value of the variable s in the given equation. This helped Vue answer his question by providing a numerical value for the amount of time that the ball was in the air when it was 54 feet above the ground.
Please help, select all the perfect squares

Answers
Answer:
9 , 16x^2 , 4z and 100y^2 are perfect Squares!
_____________________________________
What are Perfect Squares?
A perfect square is a number that can be expressed as the product of an integer by itself or as the second exponent of an integer.
3 * 3 = 9
4 * 4 = 16
2 * 2 = 4
50 * 50 = 100
Therefore making those numbers perfect squares.
[NOTE: The numbers that are squared are still perfect squared, just a larger version!]
More information on perfect squares:
https://brainly.com/question/17735980?referrer=searchResults
Have a WONDERFUL day! (:
Answer:
Step-by-step explanation:
Perfect squares are: 100y^2, 16x^2, and 9
sqrt of 100y^2 is 10y
sqrt of 16x^2 is 4x
sqrt of 9 is 3
write each equation in vertex form. then identify the vertex, axis of symmetry and direction of opening. y=x^2+8x+\:18 , y=-\:x^2\:\:12x\:-\:36 and y=2x^2\:+\:12x\:+\:13
Answers
The equation in vertex form is y = 2(x+3)² + 1. The vertex is (-3,1), the axis of symmetry is x = -3, and the direction of opening is upwards.
The vertex form of the equation is y = a(x-h)^2 + k, where (h, k) is the vertex. The axis of symmetry is x = h, and the direction of opening is determined by the value of a.
Using this formula, let us write each equation in vertex form and then identify the vertex, axis of symmetry, and direction of opening.
1. y = x² + 8x + 18
To write this equation in vertex form, we need to complete the square. y = x² + 8x + 18 is equivalent to y = (x+4)² - 2. Therefore, the equation in vertex form is y = (x+4)² - 2.
The vertex is (-4,-2), the axis of symmetry is x = -4, and the direction of opening is upwards.2
. y = -x² - 12x - 36To write this equation in vertex form, we need to complete the square. y = -x² - 12x - 36 is equivalent to y = -(x+6)² - 12. Therefore, the equation in vertex form is y = -(x+6)² - 12.
The vertex is (-6,-12), the axis of symmetry is x = -6, and the direction of opening is downwards.3. y = 2x² + 12x + 13To write this equation in vertex form, we need to complete the square. y = 2x² + 12x + 13 is equivalent to y = 2(x+3)² + 1.
To learn more about : vertex form
https://brainly.com/question/31546205
#SPJ8
Use a line integral to find the area of the region R. R : region bounded by the graphs of y=3x and y=4−x^2
Answers
Given that the region bounded by the graphs of y = 3x and y = 4 − x².Let's find the intersection points of these two curves:y = 3xand y = 4 - x²⇒ 3x = 4 - x²⇒ x² + 3x - 4 = 0⇒ x² + 4x - x - 4 = 0⇒ x(x + 4) - 1(x + 4) = 0⇒ (x + 4) (x - 1) = 0⇒ x = -4 or 1
We have to check the interval for x: -4 ≤ x ≤ 1For finding the area of the region R by using a line integral. Firstly, we need to parameterize the region R.
Let's take P(x,y) as a point on R and the parameterization of R is given by:r(t) = ⟨t, 3t⟩ for -4 ≤ t ≤ 1The limits are -4 and 1 as discussed above.Now, let's calculate dr/dt as follows:r'(t) = ⟨1, 3⟩
Area of the region R can be computed as follows:A = ∫ᵧx F(x,y) dywhere, F(x,y) = xand the limits for y are:y = 3x ≤ y ≤ 4 - x² = 3x ≤ y ≤ 4 - x²The integral becomes:A = ∫₋₄¹ x ∫₃x⁴₋ₓ² dx dy⇒ A = ∫₋₄¹ ∫₀ⁿ x dy dx
Where n = 4 - x²So, integrating with respect to y and x:A = ∫₋₄¹ xy |₀ⁿ dx= ∫₋₄¹ x(4-x²-3x) dx= ∫₋₄¹ -x³+4x dx= [(-x⁴/4)+2x²]₋₄¹= (1/4)+32= 33/4 sq unitsThe area of the region R is 33/4 sq units.
To know more about integrating Visit:
https://brainly.com/question/30900582
#SPJ11
In the diagram below, the cone has a radius of 9 centimeters and a slant height of 15 centimeters.
image 134fcf7d1dc04fbbb16d3bc2b8f9a75f
What is the volume of the cone?
Responses
324π cm3
324 π cm 3
405π cm3
405 π cm 3
972π cm3
972 π cm 3
1,215π cm3
Answers
Answer:
405π cm3
Step-by-step explanation:
A drum of petrol is 3/4 full . when 30 litres is drawn from it , it is 7/12 , find the capacity of the drum.
Answers
Answer:
The drum capacity is 180 liters.
Step-by-step explanation:
Let the capacity of the drum be c. Then the contents of the drum at the beginning are (3/4)c, and
if 30 liters are drawn out, then the contents are (3/4)c - 30 liters = (7/12)c.
Here the LCD is 12, and so we have (9/12)c - (7/12)c = 30 liters, or
(2/12)c = 30 liters, or c = (12/2)(30 liters) = 180 liters
The drum capacity is 180 liters.
Answer:
The capacity of the drum is 180 liters
Step-by-step explanation:
3/4x - 30 = 7/12x
3/4x - 7/12x = 30
9/12x - 7/12x = 30
2/12x = 30
1/6x = 30
x = 30*6
x = 180 liters
Find the slope of the line. Use the two points shown.


Answers
Answer:
The slope is 2.
Step-by-step explanation:
slope = rise/run
= 1-(-5) / 2-(-1)
= 6/3 = 2
Therefore, the slope is 2.