a play starts at 7:30pm, first act last 46 minutes, interval lasts 20 minutes. second act lasts 53 minutes, what time does the second act end?
Answers
Answer:
9:thirty one
Step-by-step explanation:
Add 46 twenty and 5three then add the answer in 7:thirty
Related Questions
At noon, Trevor and Kim start running from the same point. Trevor runs east at a speed of 8 km/h and Kim runs west at a speed of 6 km/h. At what time will they be 21 km apart?
Answers
Trevor and Kim will be situated 21 kilometers apart from each other at 1:30 PM. They will be separated by a distance of 21 km when the clock strikes 1:30 in the afternoon.
To determine at what time Trevor and Kim will be 21 km apart, we can set up a distance-time equation based on their relative speeds and distances.
Let's assume that t represents the time elapsed in hours since noon. At time t, Trevor would have traveled a distance of 8t km, while Kim would have traveled a distance of 6t km in the opposite direction.
Since they are running in opposite directions, the total distance between them is the sum of the distances they have traveled:
Total distance = 8t + 6t
We want to find the time when this total distance equals 21 km:
8t + 6t = 21
Combining like terms, we have:
14t = 21
To solve for t, we divide both sides of the equation by 14:
t = 21 / 14
Simplifying, we find:
t = 3 / 2
So, they will be 21 km apart after 3/2 hours, which is equivalent to 1 hour and 30 minutes.
Therefore, Trevor and Kim will be 21 km apart at 1:30 PM.
For more such question on distance . visit :
https://brainly.com/question/30395212
#SPJ8
A circle has a diameter of 20 cm. Find the area of the circle, leaving
π in your answer.
Include units in your answer.
Answers
If circle has a diameter of 20 cm, the area of the circle is 100π square centimeters.
The area of a circle can be calculated using the formula:
A = πr²
where A is the area, π (pi) is a mathematical constant that represents the ratio of the circumference of a circle to its diameter (approximately 3.14), and r is the radius of the circle.
In this case, we are given the diameter of the circle, which is 20 cm. To find the radius, we can divide the diameter by 2:
r = d/2 = 20/2 = 10 cm
Now that we know the radius, we can substitute it into the formula for the area:
A = πr² = π(10)² = 100π
We leave π in the answer since the question specifies to do so.
It's important to include units in our answer to indicate the quantity being measured. In this case, the area is measured in square centimeters (cm²), which is a unit of area.
To learn more about area click on,
https://brainly.com/question/19784529
#SPJ1
In a Chi-Square test, which of the following is NOT true? If the chi squared test statistic is large, the P-value will be small. Samples are drawn from different populations and we wish to determine whether these populations have the same proportions of the characteristics being considered. Small values of the chi squared test statistic would lead to a decision to reject the null hypothesis. The null hypothesis is that the different populations have the same proportions of specified characteristics.
Answers
The statement that is NOT true in a Chi-Square test is "Small values of the chi squared test statistic would lead to a decision to reject the null hypothesis."
This is because if the test statistic is small, it means that the observed values are close to the expected values, and there is no significant difference between the populations. Therefore, a small test statistic would lead to a failure to reject the null hypothesis. In a Chi-Square test, we compare the proportions of specified characteristics in different populations, and we wish to determine whether they are the same or not. If the test statistic is large, it means that the observed values are significantly different from the expected values, and we have evidence to reject the null hypothesis. Finally, the P-value will be small if the test statistic is large, indicating strong evidence against the null hypothesis.
Learn more about hypothesis here:
https://brainly.com/question/31319397
#SPJ11
Hint(s) o Use 6.87 days as a planning value for the population standard deviation. a. Assuming 95% confidence, what sample size would be required to obtain a margin of error of 0.5 days? Do not round intermediate calculations. Round your answer up to the nearest whole number. b. If the precision statement was made with 90% confidence, what sample size would be required to obtain a margin of error of 2 days?
Answers
To obtain a margin of error of 0.5 days with 95% confidence, a sample size of 738 would be required. To obtain a margin of error of 2 days with 90% confidence, a sample size of 127 would be required.
a. The required sample size for a given margin of error, we can use the formula:
n = (Z * σ / E)^2
Where:
n = required sample size
Z = Z-score corresponding to the desired confidence level (in this case, 95% confidence corresponds to a Z-score of approximately 1.96)
σ = population standard deviation
E = margin of error
Given:
Population standard deviation (σ) = 6.87 days
Margin of error (E) = 0.5 days
Confidence level = 95% (Z-score ≈ 1.96)
Substituting these values into the formula, we can solve for n:
n = (1.96 * 6.87 / 0.5)^2
n = 27.143^2
n ≈ 737.742
Rounding up to the nearest whole number, the required sample size is approximately 738.
b. Similarly, for a 90% confidence level, the Z-score is approximately 1.645. We can use the same formula to calculate the required sample size:
n = (Z * σ / E)^2
Given:
Population standard deviation (σ) = 6.87 days
Margin of error (E) = 2 days
Confidence level = 90% (Z-score ≈ 1.645)
Substituting these values into the formula, we can solve for n:
n = (1.645 * 6.87 / 2)^2
n = 11.256^2
n ≈ 126.485
Rounding up to the nearest whole number, the required sample size is approximately 127.
To learn more about sample size refer here:
https://brainly.com/question/31734526#
#SPJ11
a rectangular solid (with a square base) has a surface area of 433.5 square centimeters. find the dimensions that will result in a solid with maximum volume.
Answers
The dimensions that will result in a solid with maximum volume are approximately x = 12.02 centimeters and h = 5.01 centimeters.
Let the side of the square base be x, and let the height of the rectangular solid be h. Then, the surface area of the solid is given by:
Surface area = area of base + area of front + area of back + area of left + area of right
Surface area = x² + 2xh + 2xh + 2xh + 2xh = x² + 8xh
We are given that the surface area is 433.5 square centimeters, so we can write: x² + 8xh = 433.5
We want to find the dimensions that will result in a solid with maximum volume. The volume of the solid is given by:
Volume = area of base × height = x² × h
We can use the surface area equation to solve for h in terms of x:
x² + 8xh = 433.5
h = (433.5 - x²)/(8x)
Substituting this expression for h into the volume equation, we get:
Volume = x² × (433.5 - x²)/(8x) = (433.5x - x³)/8
To find the maximum volume, we need to find the value of x that maximizes this expression. To do this, we can take the derivative of the expression with respect to x, set it equal to zero, and solve for x:
d(Volume)/dx = (433.5 - 3x²)/8 = 0
433.5 - 3x² = 0
x² = 144.5
x = sqrt(144.5) ≈ 12.02
We can check that this is a maximum by computing the second derivative of the volume expression with respect to x:
d²(Volume)/dx² = -3x/4
At x = sqrt(144.5), this is negative, which means that the volume is maximized at x = sqrt(144.5).
Substituting x = sqrt(144.5) into the expression for h, we get:
h = (433.5 - (sqrt(144.5))²)/(8×sqrt(144.5))
h = 433.5/(8×sqrt(144.5)) - sqrt(144.5)/8
h = 5.01
Learn more about volume here:
https://brainly.com/question/6286323
#SPJ11
The dimensions of the rectangular solid that will result in a maximum volume are approximately.\(6.34 cm \times 9.03 cm \times 9.03 cm.\)
Let's assume that the length, width, and height of the rectangular solid are all equal to x, so the base of the solid is a square.
The surface area of the rectangular solid can be expressed as:
\(SA = 2xy + 2xz + 2yz\)
Substituting x for y and z, we get:
\(SA = 2x^2 + 4xy\)
We are given that the surface area is 433.5 square centimeters, so:
\(2x^2 + 4xy = 433.5\)
Simplifying, we get:
\(x^2 + 2xy - 216.75 = 0\)
Using the quadratic formula to solve for y, we get:
\(y = (-2x\± \sqrt (4x^2 + 4(216.75)))/2\)
\(y = -x \± \sqrt (x^2 + 216.75)\)
Since the base of the rectangular solid is a square, we know that y = z. So:
\(z = -x \± \sqrt(x^2 + 216.75)\)
The volume of the rectangular solid is given by:
\(V = x^2y\)
Substituting y for\(-x + \sqrt (x^2 + 216.75),\) we get:
\(V = x^2(-x + \sqrt(x^2 + 216.75))\)
Expanding and simplifying, we get:
\(V = -x^3 + x^2\sqrt(x^2 + 216.75)\)
The dimensions that will result in a solid with maximum volume, we need to find the value of x that maximizes the volume V.
We can do this by taking the derivative of V with respect to x, setting it equal to zero, and solving for x:
\(dV/dx = -3x^2 + 2x\sqrt(x^2 + 216.75) + x^2/(2\sqrt (x^2 + 216.75)) = 0\)
Multiplying both sides by \(2\sqrt (x^2 + 216.75)\) to eliminate the denominator, we get:
\(-6x^2\sqrt (x^2 + 216.75) + 4x(x^2 + 216.75) + x^3 = 0\)
Simplifying, we get:
\(x^3 - 6x^2\sqrt (x^2 + 216.75) + 4x(x^2 + 216.75) = 0\)
We can solve this equation numerically using a graphing calculator or computer software.
\(The solution is approximately x = 6.34 centimeters.\)
Substituting x = 6.34 into the expression for y and z, we get:
\(y = z \approx 9.03 centimeters\)
For similar questions on rectangular
https://brainly.com/question/19819849
#SPJ11
Solve 2x<10. Explain how to find the solution set.
Answers
Answer:
X<5
Step-by-step explanation:
Divide by 2
Answer=5
Step-by-step explanation:
You can solve this question step by step as follows;
here
2x<10
place 2 to another side and you know it divides 10
or, x<10/2
or,x<5
therefore the answer is 5
7 plus a number m is more than 5
Answers
Answer:
Step-by-step explanation:
7+m>5
Answer:
m = -2
Step-by-step explanation:
yes.
LMNO id a parallelogram. If NM =x +30 and OL=4x +9, find the value of X NM AND OL
Answers
Therefore , the solution of the given problem of parallelograms comes out to be NM and OL both equal 37.
What is parallelograms?
In Euclidean mathematics, a parallelogram is actually a simple hexagon with two distinct groups and equal distances. A specific kind of quadrilateral called a parallelogram is formed when both sets of sides equally share a horizontal path. Parallelograms come in four different varieties, three of which are mutually exclusive.
Here,
Since LMNO is a parallelogram, we know that the lengths of the opposing sides are identical. Therefore, we can equalize the NM and OL formulas, then solve for x:
=> OL = 4x + 9 and
=> NM = x + 30
=> OL = x + 30
=> 4x + 9 = NM
=> 3x = 21
=> x = 7
We have thus established that x = 7. In order to discover the values for NM and OL, we can put this value back into the expressions for those variables:
=> NM = x + 30 = 7 + 30 = 37
=> OL = 4x + 9 = 4(7) + 9 = 37
As a result, NM and OL both equal 37.
To know more about parallelograms visit:
https://brainly.com/question/29147156
#SPJ1
can someone answer page 3 question 3, page 5 question 3, all of page 6
Answers
The answers to the questions involving trigonometry are: 90, BC/AB ÷ BC/AB = 1, g = 6.5, <I = 62 degrees, h= 13.8, 12.0, x = 6.8, x = 66.4, 160.6, The pole = 6.7
What is trigonometrical ratios?Trigonometric ratios are special measurements of a right triangle, defined as the ratios of the sides of a right-angled triangle. There are three common trigonometric ratios: sine, cosine, and tangent
For page 3 question 3,
a) <A + <B = 90 since <C = right angle
b) SinA = BC/AB and CosB = BC/AB
The ratio of the two angles BC/AB ÷ BC/AB = 1
I notice that the ratio of sinA and cosB gives 1
b) The ratio of CosA and SinB will give
BC/AB ÷ BC/AB
= BC/AB * AB/BC = 1
For page 5 number 3
Tan28 = g/i
g/12.2 = tan28
cross multiplying to have
g = 12.2*tan28
g = 12.2 * 0.5317
g = 6.5
b) the angle I is given as 90-28 degrees
<I = 62 degrees
To find the side h we use the Pythagoras theorem
h² = (12.2)² + (6.5)²
h² = 148.84 +42.25
h²= 191.09
h=√191.09
h= 13.8
For page 6
1) Sin42 = x/18
x=18*sin42
x = 18*0.6691
x = 12.0
2) cos28 = 6/x
xcos28 = 6
x = 6/cos28
x [= 6/0.8829
x = 6.8
3) Tan63 = x/34
x = 34*tan63
x= 34*1.9526
x = 66.4
4) Sin50 123/x
xsin50 = 123
x = 123/sin50
x = 123/0.7660
x =160.6
5) Sin57 = P/8
Pole = 8sin57
the pole = 8*0.8387
The pole = 6.7
Learn more about trigonometrical ratios on https://brainly.com/question/23130410
#SPJ1
In Fig. 7.2, a find the value of y when x = -2-5,

Answers
Answer:
Given equation: y = x² + 2x - 3
If you wish to find the values of y when x = -2 and x = -5:
When x = -2:
⇒ y = (-2)² + 2(-2) - 3
⇒ y = 4 - 4 - 3
⇒ y = -3
When x = -5:
⇒ y = (-5)² + 2(-5) - 3
⇒ y = 25 - 10 - 3
⇒ y = 12
If you wish to find the value of y when x = -2-5:
When x = -2-5 ⇒ x = -7
⇒ y = (-7)² + 2(-7) - 3
⇒ y = 49 - 14 - 3
⇒ y = 32
Answer:
y = 32
Step-by-step explanation:
Given :-
y = x² + 2x - 3
x = -2-5 = -7
To Find :-
y
Inputting the value of x :
y = (-7)² + 2(-7) - 3
y = 49 - 17
Solution :-
y = 32
The 3rd term of a a G.P is 18 and the 7th term is 32/9. Find the G.P
Answers
The G.P. of a term is 256/243.
To find out the G.P. for the 3rd term:
Let us consider the 1st term to be 'a'.
So, \(ar^{2}=18\) ....... Equation (1)
Also \(ar^{6} = \frac{32}{9}\) ..... Equation (2)
Dividing (2) by (1), we get,
\(\frac{ar^{6}}{ar^{2}} = \frac{32}{162}\)
\(r^{4}\) = 16/81.
r = 2/3.
Putting r in equation (1) than we will get
a = 81/2.
So, 10th term = \(ar^{9}\)
= (81/2) ×(512/19683)
= 256/243.
Hence the answer is the G.P. of a term is 256/243.
To learn more about Probability click here https://brainly.com/question/24756209
#SPJ9
What is it pls tell me

Answers
sorry if I’m wrong tho
please answer and explain the link below

Answers
Thanks for the points hope you'll understand
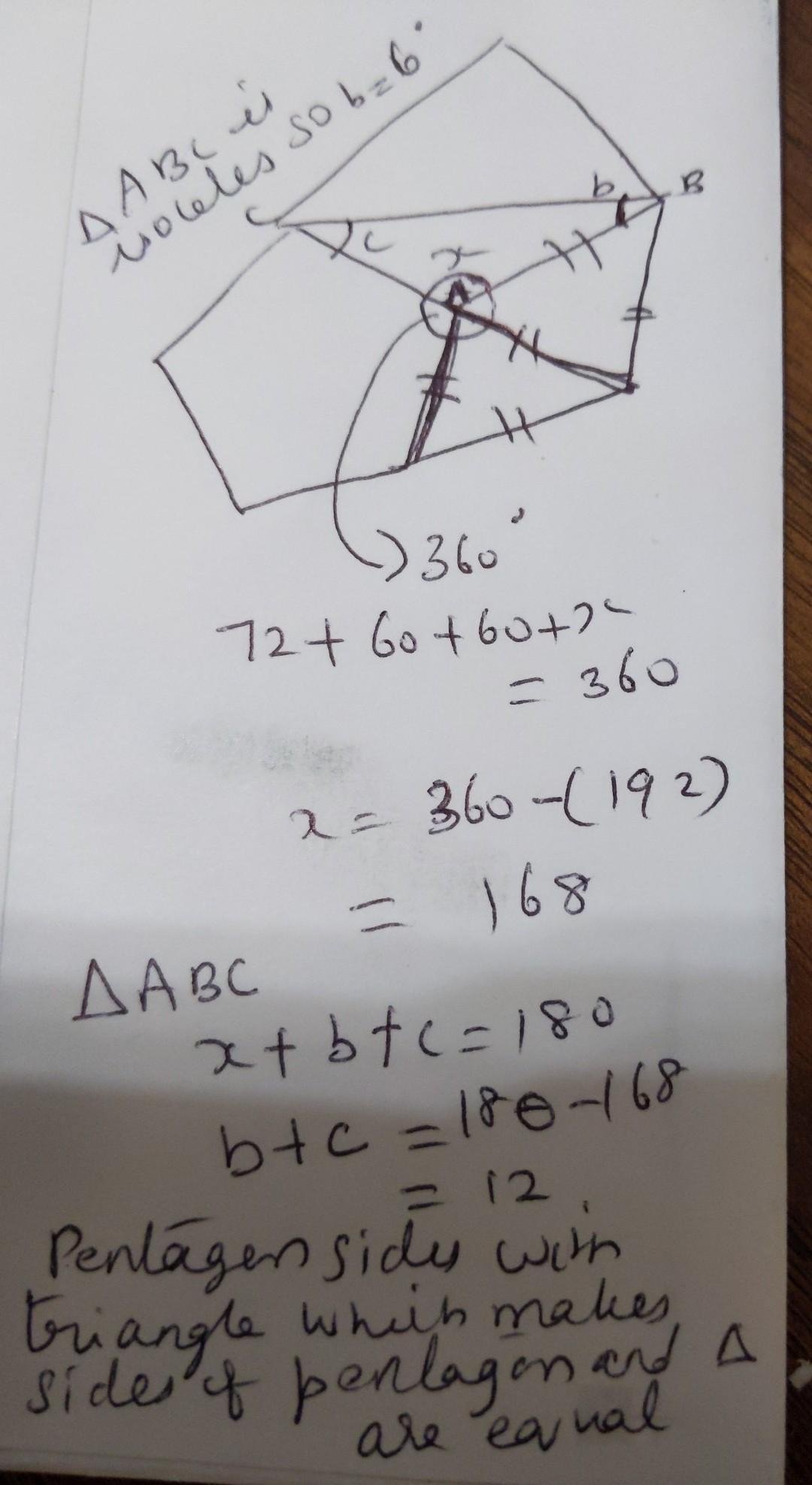
four grey regular polygons join together as shown in the diagram
please answer part b

Answers
Answer:
a=72° b = 6°
Step-by-step explanation:
answer is in pic
hello people ~
Sketch the graph of y = 4 cos 3x° + 7
Answers
Answer:
\(\sf\fbox\red{Answer:-}\)
The answer in the attachment may help uh
\(\small\fbox{\blue{\underline{mαrk \; mє \; вrαínlíєѕt \; plєαѕє ♥}}}\)

\(\sf \bold{\:y\:=\:4\:cos\:3x\:+\:7}\)
\(\sf \sf{Y\:Intercepts}:\:\left(0,\:11\right)\)\(\sf \sf{X\:Intercepts}:\:\left none\)\(\sf \sf \sf{Asymptotes}:\:\left none\)\(\sf \sf{Domain}:\:\left(-\infty \: < x < \infty )\)graph attached below:
[ fieryanswererft ]

Which of the of the following statements is true with respect to a simple linear regression model? a. the stronger the linear relationship between two variables, the closer the correlation coefficient will be to 1. O b. if the correlation coefficient between the x and y variables is negative, the sign on the regression slope will also be negative. O C. if the correlation coefficient between the dependent and independent variable is determined to be significant, the regression model for y given x will also be significant. O d. all of the above is true. e. none of the above is true.
Answers
Answer:
d. All of the above are true
Step-by-step explanation:
All of the following statements,
a. the stronger the linear relationship between two variables, the closer the correlation coefficient will be to 1.
b. if the correlation coefficient between the x and y variables is negative, the sign on the regression slope will also be negative.
C. if the correlation coefficient between the dependent and independent variable is determined to be significant, the regression model for y given x will also be significant.
are true
Jeremiah makes 25% of the three-point shots he attempts. For a warm up, Jeremiah likes to shoot three-point shots until he successfully makes one. Let M be the number of shots it takes Jeremiah to successfully make his first three-point shot. Assume that the results of each shot are independent. Find the probability that Jeremiah's first successful shot occurs on his 3rd attempt. You may round your answer to the nearest hundredth. P(M=3)=
Answers
Answer: .14
Step-by-step explanation: Khan Academy
Answer:
0.14
Step-by-step explanation:
First off, please read clearly.
This problem is asking for the probability that (M = 3).
The correct answer for this P(M = 3) problem is 0.14 through Khan Academy.
Even when you solve it, it is 0.14. The equation would be zero point twenty-five multiplied by parenthesis one minus zero point twenty-five closed parenthesis to the power of two. Written out the equation would be the following:
0.25x(1-0.25)^2
*** DO NOT MIX THIS UP WITH A VERY SIMILAR PROBLEM TO THIS. ***
There is a problem using this same Jeremiah situation but it asks for P(M < 4).
If you want the answer for P(M < 4) it is 0.58 so
P(M < 4) = 0.58
And another Jeremiah problem that asks for P(M > 6).
If you want the answer for P(M > 6) it is 0.18 so
P(M > 6) = 0.18
Have a nice day :)
Solve the matrix equation.
2
-3
8
16
-1 -5
X
II
-4
3
0 0
-5
2
-4
a.
c.
8
-4
3
3
-4
-4
عا
3
-9
5
-4.
- 9
5
4.
5
b.
d.
-4.
3
-8 4
3
3
89
-9 1
4
95 -4

Answers
Answer:
a is the correct answer
Step-by-step explanation:
\( \binom{8 \: \: \: - 4 \: \: \: 3}{ - 9 \: \: \: 5 \: \: \: - 4} \)
A social security number contains nine digits, such as 914-47-2245. How many different social security numbers can be formed?
Answers
The number of different social security numbers that can be formed is 3628800.
Given that :
A social security number contains nine digits, such as 914-47-2245.
There are digits 0,1,2,....,9.
So there are 10 numbers in total.
So we can select 9 numbers from a total of 10 numbers.
Using permutation, total numbers is :
P(10, 9) = 10! / (10 - 9)!
= 10!
= 3628800
Hence the total number of security numbers that can be formed is 3628800.
Learn more about Permutations here :
https://brainly.com/question/32683496
#SPJ4
Evan practices the piano 329 minutesbc in 1 weeks. Assuming he practices the same amount every week, how many minutes would he practice in 2 weeks?
Answers
The number of minutes of practice in two weeks is 658.
What is an expression?An expression is a way of writing a statement with more than two variables or numbers with operations such as addition, subtraction, multiplication, and division.
Example: 2 + 3x + 4y = 7 is an expression.
We have,
Total minutes of practice in one week = 329.
Total minutes of practice in two weeks.
= 2 x 329
= 658 minutes.
Thus,
658 minutes was the practice in two weeks.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
0.75x — 13 = 2
What's the value of x
Answers
Answer:
The value of x is 20.
Step-by-step explanation:
The steps are :
0.75x - 13 = 2
0.75x = 2 + 13
0.75x = 15
x = 15 ÷ 0.75
x = 20
A 2010 u.s. census bureau report indicated there are 4,229,138 residents of indiana aged 25 and older. what percentage of the residents aged 25 and older have a degree if there are 326,036 residents with an associate's degree, 623,200 with a bachelor's degree, and 348,807 with either a graduate or professional degree? write your answer as a percent rounded to the nearest whole number.
Answers
Among the 4,229,138 residents of Indiana aged 25 and older, the percentage of the residents aged 25 and older that have a degree is 31 %.
Percentage, which was adapted from the Latin word "per centum", which means "by the hundred", is a fraction or a ratio in which the value of whole is always 100. It is represented by the symbol "%".
The formula to get the percentage is:
Percentage = (Value / Total Value) × 100
Getting first the total value of the degree holders: 326,036 have an associate's degree, 623,200 have a bachelor's degree, and 348,807 have either a graduate or professional degree
residents with degree = 326,036 + 623,200 + 348,807
residents with degree = 1,298,043
If the total value of the residents aged 25 and older is 4,229,138 and among them, 1,298,043 have a degree, getting its percentage using the formula:
Percentage = (Value / Total Value) × 100
Percentage = (1,298,043 / 4,229,138) × 100
Percentage = (0.3069285041) × 100
Percentage = 30.69 %
Rounding off to the nearest whole number,
Percentage = 31 %
To learn more about percentages: brainly.com/question/24304697
#SPJ4
√9pr / (pr)^-3/2 =
A. √3pr
B. 3/pr
C. 3√pr
D. 3pr
E. 3p²r²
Answers
Answer:
E
Step-by-step explanation:
=√9pr / (pr)^-3/2
=3√(pr) × (pr)^3/2
= 3p²r²
Answer:
E. 3p²r²
Step-by-step explanation:
√9pr / (pr)^-3/2=
3(pr)^1/2*(pr)^3/2=
3(pr)^(1/2+3/2)=
3(pr)^2=3p^2r^2
A cook wants to make enough cookies for 150 students. The cookie recipe makes 1 dozen cookies. A dozen equals 12 cookies.
How many batches does the cook need to make if each student gets one cookie?
Answers
Answer:
12.5
Step-by-step explanation:
150 / 12 = 12.5
(I'm not the best at explaining-)
A 2% solution of _______________ has been moderately effective for about 50% of men who have used it.
Answers
A 2% solution of Minoxidil has been moderately effective for about 50% of men who have used it. Minoxidil is a vasodilator that was initially developed to manage hypertension.
Minoxidil, a medication that is applied topically, is used to cure hair loss in males and females, although it is more often used in men. It works by stimulating hair growth and slowing down hair loss.Minoxidil, a vasodilator, increases blood flow to the hair follicles, allowing them to produce thicker and longer hair. It is sold under various brand names, including Rogaine, Regaine, and Avacor Physician's Formulation, and is available in various strengths, including 2% and 5%.Minoxidil is more effective in treating androgenetic alopecia, also known.
As male pattern baldness, than other types of hair loss. It is believed that minoxidil promotes hair growth by increasing the diameter of the hair shaft, resulting in thicker and longer hair growth.Minoxidil is used to treat male and female pattern baldness (androgenetic alopecia) by applying it topically to the scalp. However, like any medication, there may be side effects, such as skin irritation, burning, or itching. As a result, it is recommended that people use it under the supervision of a physician.
To know more about developed visit:
https://brainly.com/question/31944410
#SPJ11
What is the solution set for the inequality Negative one-fourthx2(x – 4)(x +5) ≤ 13?
Answers
Answer:
c
Step-by-step explanation:
Answer:
c
Step-by-step explanation:
How do I get the exact value of sin 480?
Answers
Step 1
Remove full rotations of 360 degrees until the angle is between 0 and 360 degrees
\(480-360=120^o\)Step 2
Hence, we find sin 120 using reference angles in the first quadrant
\(\begin{gathered} \sin \text{ 60=}\frac{\sqrt[]{3}}{2} \\ \text{Hence} \\ \sin 120=\frac{\sqrt[]{3}}{2} \end{gathered}\)Therefore,
\(\begin{gathered} \sin 480=\sin 120=\sin 60=\frac{\sqrt[]{3}}{2} \\ \sin \text{ 480=}\frac{\sqrt[]{3}}{2} \end{gathered}\)Answer sin 480 =(√3)/2
A linear transformation is a special type of function_ b If A is a 3 x 5 matrix and T is & transformation defined by T(x) = Ax, then the domain of T is R' If Ais an m Xn matrix, then the range of the transforma- tion X +> Ax is Rm d. Every linear transformation is a matrix transformation_ A transformation T is linear if and only if T(cv+ C2V2) = CT() + CT (V2) for all Vq and Vz in the domain of T and for all scalars € and C2:
Answers
According to the question For a) This statement is correct. For b) statement is incorrect. For c) statement is correct. For d) statement is incorrect and For e) This statement is correct.
a. A linear transformation is a special type of function.
This statement is correct. A linear transformation is a function between vector spaces that preserves the vector addition and scalar multiplication operations. In other words, it satisfies two properties: preservation of addition
\(\[T(u + v) = T(u) + T(v)\]\)
and preservation of scalar multiplication
\(\[T(cu) = cT(u)\]\)
where \(\(T\)\) is the linear transformation, \(\(u\)\) and \(\(v\)\) are vectors, and \(\(c\)\) is a scalar.
b. If \(\(A\)\) is a \(\(3 \times 5\)\) matrix and \(\(T\)\) is a transformation defined by \(\(T(x) = Ax\),\) then the domain of \(\(T\)\) is \(\(\mathbb{R}^5\).\)
This statement is incorrect. The domain of the transformation \(\(T\)\) is determined by the size of the input vectors, which in this case is determined by the number of columns of matrix \(\(A\)\). Since \(\(A\)\) is a \(\(3 \times 5\)\) matrix, the domain of \(\(T\)\) is \(\(\mathbb{R}^5\), not \(\mathbb{R}\).\)
c. If \(\(A\)\) is an \(\(m \times n\)\) matrix, then the range of the transformation \(\(x \rightarrow Ax\)\) is \(\(\mathbb{R}^m\).\)
This statement is correct. The range of the transformation \(\(x \rightarrow Ax\)\) is the set of all possible outputs obtained by multiplying the matrix \(A\)\) with the input vectors \(\(x\).\) Since \(\(A\)\) is an \(\(m \times n\)\) matrix, the resulting vectors will have \(\(m\)\) dimensions. Therefore, the range of the transformation is \(\(\mathbb{R}^m\).\)
d. Every linear transformation is a matrix transformation.
This statement is incorrect. While every matrix transformation is a linear transformation (since matrix multiplication satisfies the properties of linearity), not every linear transformation can be represented by a matrix. Linear transformations can have various forms and may not always be expressible as matrix multiplication.
e. A transformation \(\(T\)\) is linear if and only if \(\(T(cv + c_2v_2) = cT(v_1) + c_2T(v_2)\)\) for all \(\(v_1\)\) and \(\(v_2\)\) in the domain of \(\(T\)\) and for all scalars \(\(c\)\) and \(\(c_2\).\)
This statement is correct. This equation represents the linearity property of a transformation. A transformation \(\(T\)\) is linear if and only if it satisfies this equation, which states that the transformation of a linear combination of two vectors is equal to the linear combination of the transformed vectors.
To know more about vectors visit-
brainly.com/question/32952227
#SPJ11
Find the x 2x - 3 = 1
Answers
Answer:
x=2
Step-by-step explanation:
2x - 3 = 1
Add 3 to each side
2x - 3+3 = 1+3
2x = 4
Divide by 2
2x/2 = 4/2
x = 2
Answer:
2=x
Step-by-step explanation:
2x-3=1
+3 +3
2x=4
4/2=2
2=x
2X-Y=4
x=4-y
please explain each step
Answers
Step-by-step explanation:
2X-Y=4 ---------(1)
x=4-y---------(2)
since x = 4 – y just substitute for eqn 1
2(4–y) – y = 4
8 – 2y –y=4
8 –3y = 4
–3y=4–8
–3y=–4
y=–4/–3
y= 4/3
since y = 4/3 just substitute for y in eqn (2)
x=4–4/3
multiply both sides by 3
3x=12–4
3x=8
x=8/3 or 2 2/3