A model rocket is launched with an initial upward velocity of 126. The rocket's height (in feet) after seconds is given by the following. Find all values of for which the rocket's height is 50 feet.
Answers
At time t = 0.4191 and t = 7.456, rocket was at the height of 50 feet;
Given equation; h = 126t - 16t²;
when rocket's height is 50 feet;
126t - 16t² = 50
16t² - 126t + 50 = 0
Using quadratic formula;
t = {126 ±√(-126)² - (4)(16)(50)}/2(16)
After solving; t =0.4191 and t = 7.456
Therefore, at time t = 0.4191 and t = 7.456, rocket was at the height of 50 feet;
To learn more about quadratic formula; visit: https://brainly.com/question/9300679
#SPJ9
Related Questions
Anna is a sales person who has jobs this week in cities within North Carolina and South Carolina. On a map, these two cities are 50 centimeters apart. The map uses a scale of 2 centimeters = 4 kilometers. What is the actual distance between these cities?Gavin goes to the market and buys one rectangle shaped board. The length of the board is 16 cm and the width of the board is 10 cm. If he wants to add a 2 cm wooden border around the board, what will be the area of the rectangle board?
Answers
Anna is a sales person who has jobs this week in cities within North Carolina and South Carolina. On a map, these two cities are 50 centimeters apart. The map uses a scale of 2 centimeters = 4 kilometers. What is the actual distance between these cities?
Applying the Rule of Three that allows you to solve problems based on proportions.
Distance of the two cities= 50 cm
The map uses a scale of 2 centimeters = 4 kilometers.
Answer: The actual distance between these cities is 100 km

The quadratic function y = -x2 + 10x - 8 models the height of a trestle on a bridge. The x-axis represents ground level.
To find where the section of the bridge meets ground level, solve 0 = -x2 + 10x - 8.
Where does this section of the bridge meet ground level?
Answers
Answer: 0.876, 9.123
Step-by-step explanation:
The function is \(y=-x^2+10-8\)
It meets the ground level when \(y\) is 0
\(\Rightarrow -x^2+10x-8=0\\\Rightarrow x^2-10x+8=0\\\\\Rightarrow x=\dfrac{10\pm \sqrt{(-10)^2-4(1)(8)}}{2}\\\\\Rightarrow x=\dfrac{10\pm \sqrt{68}}{2}\\\\\Rightarrow x=5\pm \sqrt{17}\\\Rightarrow x=0.876,\ 9.123\)
Thus, it touches the ground at two points given above
XZ.P Point P(-7, 2) is mapped onto P¹ (3, -11) by the reflection y=mx+c. find the values of the constants m and c.
Answers
The values of the constants m and c include the following:
m = -1.3
c = 7.1
What is the slope-intercept form?In Mathematics and Geometry, the slope-intercept form of the equation of a straight line is given by this mathematical equation;
y = mx + c
Where:
m represent the slope or rate of change.x and y are the points.c represent the y-intercept or initial value.Since the point P(-7, 2) is mapped onto P' (3, -11) by the reflection y = mx + c, we can write the following system of equations;
2 = -7m + c ...equation 1.
-11 = 3m + c ...equation 2.
By solving the system of equations simultaneously, we have:
2 = -7m - 3m - 11
11 + 2 = -10m
13 = -10m
m = -1.3
c = 7m + 2
c = 7(-1.3) + 2
c = -7.1
Read more on slope-intercept here: brainly.com/question/7889446
#SPJ1
In a study researchers reported the mean BMI for men 60 and older to be 24.7 with a standard deviation of 3.3 and the mean BMI for women 60 and older to be 23.1 with a standard deviation of 3.7. Using these values as the populations mean and standard deviation for men and women respectively, find the probability that the difference in the mean BMI (men-women) for 45 women and 50 men selected independently and at random will exceed 2.1.
Answers
Answer:
Probability that the difference in the mean BMI (men-women) for 45 women and 50 men selected independently and at random will exceed 2.1 = 0.2451
Step-by-step explanation:
The central limit theorem helps us to obtain the mean and the standard deviation of any sampling distribution.
Given that the sample was obtained from a normal distribution or an approximately normal distribution & it was obtained using random sampling techniques with each variable independent of one another and with each sample with adequate sample size,
Mean of sampling distribution (μₓ) = Population mean (μ)
Standard deviation of the sampling distribution = σₓ = (σ/√N)
where σ = population mean
N = Sample size
For the 45 women
μₓ = μ = 23.1
σₓ = (σ/√N) = (3.7/√45) = 0.552
For the 50 men
μₓ = μ = 24.7
σₓ = (σ/√N) = (3.3/√50) = 0.467
To find the probability that the difference in the mean BMI (men-women) for 45 women and 50 men selected independently and at random will exceed 2.1, we need to combine the distributions.
New distribution = (BMI of men) - (BMI of women) = x = X₁ - X₂
When independent distributions are combined, the combined mean and combined variance are given through the relation
Combined mean = Σ λᵢμᵢ
(summing all of the distributions in the manner that they are combined)
Combined variance = Σ λᵢ²σᵢ²
(summing all of the distributions in the manner that they are combined)
λ₁ = 1, λ₂ = -1
μ₁ = 24.7, μ₂ = 23.1
σ₁ = 0.467, σ₂ = 0.552
Combined mean = (Mean of men) - (Mean of women) = 24.7 - 23.1 = 1.6
Combined Variance = (1²×0.467²) + [(-1)²×(0.552²)] = 0.522793
Combined standard deviation = √0.522793 = 0.723
Probability that the difference in the mean BMI (men-women) for 45 women and 50 men selected independently and at random will exceed 2.1 = P(x > 2.1)
Note that the resulting distribution from the combination of distributions is still a normal distribution since the distributions combined were normal distributions too.
Hence, we first normalize or standardize 2.1
The standardized score for any value is the value minus the mean then divided by the standard deviation.
z = (x - μ)/σ = (2.1 - 1.6)/0.723 = 0.69
To determine the required probability
P(x > 2.1) = P(z > 0.69)
We'll use data from the normal distribution table for these probabilities
P(x > 2.1) = P(z > 0.69) = 1 - P(z ≤ 0.69)
= 1 - 0.7549
= 0.2451
Hope this Helps!!!
find the equation for the line that passes through the point (4,-3), and that is perpendicular to the line with the equation y= -3/4x-3
Answers
Answer:
hi
Step-by-step explanation:
Answer
Slope between two given points (1,3) and (2,7) is
m=
2−1
7−3
=4
Then perpendicular slope is m
1
=
4
−1
The line equation with this slope is given by
y=
4
−1
x+c.......(1)
Now, the above line passes through the point (−4,−3)
⇒−3=
4
−1
×(−4)+c
⇒c=−4
Therefore required line is 4y+x+16=0 (Substitute
′
c
′
in (1) and simplify)
Factor each.
Please help!

Answers
Answer:
1) The factors of \(x^2-3x+2=0\) are \(\mathbf{(x-1)(x-2)=0}\)
Option C is correct.
3) The factors of \(x^2+2x-8=0\) are \(\mathbf{(x-2)(x+4)=0}\)
Option B is correct.
Step-by-step explanation:
1) Factor : \(x^2-3x+2=0\)
For factoring we need to break the middle term, such that there sum is equal to middle term of expression and product is equal to product of first and last term.
The middle term : -3x
We can break them as (-2x)( -x)
Solving:
\(x^2-3x+2=0\\x^2-2x-x+2=0\\x(x-2)-1(x-2)=0\\(x-1)(x-2)=0\)
So, factors of \(x^2-3x+2=0\) are \(\mathbf{(x-1)(x-2)=0}\)
Option C is correct.
3) Factor: \(x^2+2x-8=0\)
For factoring we need to break the middle term, such that there sum is equal to middle term of expression and product is equal to product of first and last term.
The middle term : 2x
We can break them as (4x)( -2x)
Solving
\(x^2+2x-8=0\\x^2+4x-2x-8=0\\x(x+4)-2(x+4)=0\\(x-2)(x+4)=0\)
So, factors of \(x^2+2x-8=0\) are \(\mathbf{(x-2)(x+4)=0}\)
Option B is correct.
evaluate (11.6)^2 by using (a^2+b^2+2ab)
Answers
Answer:
\(134.56\)
Step-by-step explanation:
Break 11.6 into addenda.
\((11 + 0.6)\)
Apply the binomial expansion method.
\((11 + 0.6)(11 + 0.6)\)
\(11 {}^{2} = 121\)
\(2(11)(0.6) = 13.2\)
\(0.6 {}^{2} = 0.36\)
Add them all up and you get.
\(134.56\)

area of 6ft 10ft 14ft figure

Answers
Answer:
209.25
Step-by-step explanation:
Calculate the areas of the triangle, rectangle, and half circle, then add them together:
triangle = 1/2bh = 1/2(6)(10) = 30
rectangle = bh = (14)(10) = 140
half circle = 1/2πr² = 1/2(3.14)(5)² = 39.25
radius = r = D/2 = 10/2 = 5
Total area = 30 + 140 + 39.25 = 209.25
Answer:
209.25 ft²
Step-by-step explanation:
To find the total area of the figure you have to add the areas of the triangle, rectangle and the semi circle.
Area of the triangle.
\( \sf \: A = \frac{1}{2} \times base \times height \\ \sf \: A = \frac{1}{2} \times 6 \: ft \times10 \: ft \\ \sf \: A = \frac{1}{2} \times 60 \: {ft}^{2} \\ \sf \: A =30 \: {ft}^{2} \)
Area of the rectangle.
\(\sf \: A =length \times width \\ \sf \: A =14 \: ft \times 10 \: ft \\ \sf A =140 \: {ft}^{2} \)
Area of the semi circle.
\( \sf \: A = \frac{1}{2} \pi {r}^{2} \\ \sf \: A = \frac{1}{2} \times \pi \times ( \frac{10}{2}) ^{2} \\ \sf \: A = \frac{1}{2} \times \pi \times {5}^{2} \\ \sf \: A = \frac{1}{2} \times \pi \times 25 \\ \sf \: A = \frac{1}{2} \times 3.14 \times 25 \\ \sf \: A = \frac{1}{2} \times 78.5 \\ \sf \: A = 39.25 {ft}^{2} \)
Add up all the areas to find the total area.
\( \sf \: Total \: Area = 30 {ft}^{2} + 140 {ft}^{2} + 39.25 {ft}^{2} \\ = 209.25 {ft}^{2} \)
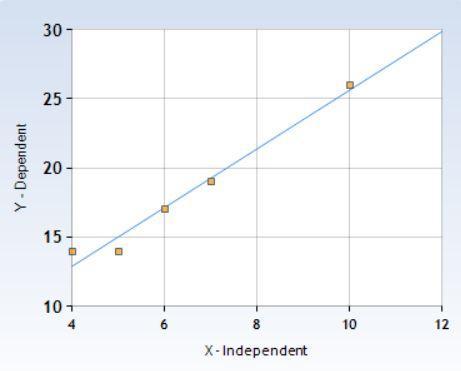
determine the equation of the line of the line of best fit from the data in the table on the right. x 4 5 6 7 10 y = 14 14 17 19 26
Answers
The equation for the line of best fit from the given data, will be y = 2.12 x + 4.42.
How to find the line of best fit ?The line of best fit would be the line that has an equal number of points above it, as the number of points beneath it.
Going by this definition, two points that would be on the line are (6, 17) and ( 7, 19 ).
The slope of this line would be:
= ( Y2 - Y1 ) / ( X 2 - X1)
= ( 19 - 17 ) / (7 - 6 )
= 2.12
The y intercept would be:
y = mx + c
19 = 2.12 (7 ) + c
c = 4.42
The equation of the line of best fit is then :
y = 2.12 x + 4.42
Find out more on line of best fit at https://brainly.com/question/17013253
#SPJ1
2 points Jason's friend George jumped off a cliff into the ocean in Acapulco while vacationing with some friends. His height as a function of time could be modeled by the function h(t)=-16t2+16t+480, where t is the time in seconds and h is the height in feet. a) What was George's height (disregard units in answer) after 5 seconds? *
Answers
we need to substitute t=5
\(h(5)=16(5^2)+16(5)+480\)\(h(5)=16(25^{})+16(5)+480\)\(h(5)=400+80+480=960\)The George's height after 5 seconds was 960
27 Answer:
Given the simple interest formula, I = Prt, solve for t
28 Answer:
Rewrite the equation so that y is a function of x:
7x + y = 13
29 Answer:
Rewrite the equation so that y is a function of x:
3x + 5y = 15
30 Answer:
Use the result in question #28 to find y when x = -1.
31 Answer:
Use the result in question #29 to find y when x = -1.
32 Answer:
Find the unit rate: 3 tablespoons for 1.5 servings.
33 Answer:
Find the unit rate: $10.99 for 12 slices of pizza.
34 Answer:
Convert the measure. Round your answer to the nearest tenth.
15 teaspoons to tablespoons (1 tablespoon = 3 teaspoons).
35 Answer:
Find the percent. Round to the nearest whole percent.
159 people in favor out of 350 people surveyed.
Answers
28. t = I / (Pr)
29. y = -(3x / 5) + (15 / 5)
30. y = -3/5 x + 3
31. y = -3/5 * -1 + 3 = 3 + 3/5 = 3.6
32. 2 tablespoons per serving
33. $0.92 per slice
34. 5 tablespoons
35. 45% (159 / 350 = 0.45 and 0.45 * 100 = 45)
What is a simple interest?Simple interest is a method of calculating the interest charge on a loan or deposit based on a constant interest rate and the original principal amount. The formula for simple interest is I = Prt, where P is the principal amount, r is the interest rate as a decimal, t is the time period in years, and I is the interest amount. In simple interest, the interest amount is calculated only on the original principal, not on any accumulated interest from prior periods.
learn more about simple interest: https://brainly.com/question/25793394
#SPJ1
a 680g patient comes in with diarrhea. the doctor orders anti-diarrhea medication at a dosage of 15 mcg/kg TID x 3 days. rhye medication concentration 50mcg/ml. What is the patients dose in MCG? What is the total volume of medication you will send home?
Answers
Answer:
dose in MCG = 10.2 mcg
Total volume to be sent home = 1.836 ml (1836μl)
Step-by-step explanation:
weight of patient = 680g
dosage in mcg of medication = 15mcg/kg
This means that
for every 1kg weight, 15mcg is given,
since 1kg = 1000g, we can also say that for every 1000g weigh, 15mcg is given.
1000g = 15mcg
1g = 15/1000 mcg = 0.015 mcg
∴ 680g = 0.015 × 680 = 10.2 mcg
Dosage in MCG = 10.2 mcg
Next, we are also told ever ml volume of the drug contains 50 mcg weight of the drug (50mcg/ml). This can also be written as:
50mcg = 1 ml
1 mcg = 1/50 ml = 0.02 ml
∴ 10.2 mcg = 10.2 × 0.02 = 0.204 ml
since the medication is to be taken TID (three times daily) for 3 days, the total number of times the drug is to be taken = 9 times.
therefore, the total volume required = 0.204 × 9 = 1.836 ml (1836 μl)
Krista designs quilts using the pattern shown. The table of values describes the shaded area of the pattern in square units, y, as a function of the length of a side,X units. Which equation describes this relationship?

Answers
The equation which describes the relationship between the side length and shaded area of the quilt is y=0.5x²
Modeling relationship between two variablesSide length, x = 1,3,4,5,8
Shaded Area, y = 0.5, 4.5, 8, 12.5, 32
The relationship can be modeled as a quadratic function. Using a graphing calculator for the quadratic function written in the form y = ax² + bx + c
a = 0.5 ; b = 0 ; c = 0
Therefore, the quadratic function can be written as y = 0.5x²
Learn more on quadratic functions ; https://brainly.com/question/1214333
#SPJ1

M Question 2 Unit 7 Chapter 10 %
https://ezto.mheducation.com/ext/map/index.html?
Account for 63859...Pay your trash bills...
Unit 7 Chapter 10 Quiz
2
Imported from inte...
Wait time
Inspection time
Process time
Seved
New folder
Imported from inte....
17 days
13 days
23 days
22 days
12 days
Navern Corporation manufactures and sells custom home elevators. From the time an order is
placed until the time the elevator is installed in the customer's home averages 87 days. This 87
days is spent as follows:
Help
Move time
Queue time
What is Navern's manufacturing cycle efficiency (MCE) for its elevators?
Seve & Exit
Su
Answers
Navern's manufacturing cycle efficiency (MCE) for its elevators is: 41.4%
How to solve the manufacturing cycle efficiencyThe formula for obtaining the manufacturing cycle efficiency is value-added time divided by the production cycle time * 100. In the data given, the process and inspection times qualify as a value-added time
Process time = 23 days
Inspection time = 13 days
Value added time = 23 + 13 = 36days
The production cycle time = Move time + process time + queue time + inspection time + wait time
= 22 + 12 + 23 + 13 + 17 days
= 87 days
So, the manufacturing efficiency time = 36/87 * 100
= 41.4%
Learn more about manufacturing efficiency here:
https://brainly.com/question/29645032
#SPJ1
Simplify (2x-3)(5x squared-2x+7)
Answers
To simplify the expression (2x-3)(5x^2-2x+7), we can use the distributive property.
First, multiply 2x by each term inside the second parentheses:
2x * 5x^2 = 10x^3
2x * -2x = -4x^2
2x * 7 = 14x
Next, multiply -3 by each term inside the second parentheses:
-3 * 5x^2 = -15x^2
-3 * -2x = 6x
-3 * 7 = -21
Combine all the resulting terms:
10x^3 - 4x^2 + 14x - 15x^2 + 6x - 21
Now, combine like terms:
10x^3 - 19x^2 + 20x - 21
So, the simplified expression is 10x^3 - 19x^2 + 20x - 21.
For such more question on parentheses
https://brainly.com/question/172904
#SPJ8
Solve the following system of equations using either Gaussian elimination or a matrix. Write your answer as a point and explain how you would check your work:

Answers
By using Matrix method it denotes that the equations are consistent and have a single solution.
Matrix method, we will use the formula, \(X=A^{-1} B\) where,
\(\[{\rm{X}} = \left[ {\begin{array}{*{20}{l}}x\\y\\z\end{array}} \right]\]\)
\(\[{A^{ - 1}} = \frac{{adjA}}{{|A|}}\]\)
\(\[{\rm{B}} = \left[ {\begin{array}{*{20}{c}}{33}\\{ - 26}\\{23}\end{array}} \right]\]\)
So, we will have to find \(A^{-1}\), for that, we will first find the determinant of matrix A, that is |A|, then we will find the cofactors of matrix A, take its transpose, and that will be Adj A.
Therefore, we will be able to get the inverse of matrix A using
\(A^{-1}\) =Adj A|A|
and hence We then substitute all the obtained values of \(A^{-1}\) and B in the main formula and do necessary calculations to get the value of x, y and z accordingly.
Complete step-by-step answer:
It is given in the question that, we have to solve the system of equations,
2x-y+4z=33
X+2y-3z=−26
-5x−3y+5z=23
Applying the matrix approach.
Therefore, the first step is to convert the supplied equations into matrix form. Thus, it can be expressed as follows.
\(\[\left[ {\begin{array}{*{20}{c}}2&{ - 1}&4\\1&2&{ - 3}\\{ - 5}&{ - 3}&5\end{array}} \right]\left[ {\begin{array}{*{20}{l}}x\\y\\z\end{array}} \right]\]\[\)\(= \left[ {\begin{array}{*{20}{c}}{33}\\{ - 26}\\{23}\end{array}} \right]\)
\(\[|{\rm{A}}| = \left[ {\begin{array}{*{20}{c}}2&{ - 1}&4\\1&2&{ - 3}\\{ - 5}&{ - 3}&5\end{array}} \right]\]\)
= 2(10+9) + 1(5-15) + 4(-3+10)
= 38-10+28
=56
Since we have |A|≠0.
Hence, it denotes that the equations are consistent and have a single solution.
To learn more about Matrix Method, visit:
https://brainly.com/question/12450320
#SPJ1
Below are the names of ten students:
Dorothy
Anthony
Harold
Margaret
Tiffany
Nancy
Angela
Paul
For the following, assume the probability of a student being chosen is the same for each student. Also, assume that
simple random sampling is being used. (If necessary, use an exact decimal value for all probabilities.)
a.) What is the probability of choosing a student whose name ends with the letter "k"?
b.) What is the probability of choosing a student whose name begins with the letter "C"?
Patrick
Jeremy
c.) What is the probability of choosing a student whose name contains the letters "m" or "M"?
d.) A Math Club is formed using these ten students, and the club must consist of seven students. How many ways
can students be assigned to the Math Club?
e.) The ten students enter an art competition where first place wins $100, second place wins $50, third place wins
$25, and fourth place wins $10. How many different ways can prizes be distributed?
It’s not multiple choice you have to work the math problem!!
Answers
Step-by-step explanation:
a probability is always the ratio
desired cases / totally possible cases
let's relist the 10 names, as there was some "mixing" going on in your text :
Dorothy
Anthony
Harold
Margaret
Tiffany
Nancy
Angela
Paul
Patrick
Jeremy
so, whatever happens, the totally possible cases are 10 (as we are only taking about these 10 names, no other name can suddenly appear in all the scenarios).
in each scenario one student is randomly chosen.
a) the probabilty to pick a student with name ending "k".
we look through the list and find only 1 student, whose name ends with "k" : Patrick.
that means the number of desired cases is 1.
and the probabilty is therefore
1/10 = 0.1
b) the probability to pick a student with name beginning "C".
we look and look and look. none of the 10 names start with a "C".
that means the number of desired cases is 0.
and the probabilty is
0/10 = 0
c) the probability that the name of the picked student contains "m" or "M".
we find 2 names : Margaret and Jeremy.
that means that the number of desired cases is 2.
and the probabilty is therefore
2/10 = 1/5 = 0.2
d) in how many ways can we pick 7 elements out of 10, when the sequence of the pulled 7 elements does not matter (e.g. ... Nancy, Paul ... is the same as ... Paul, Nancy, ...). and no student can be pulled more than once (no repetitions).
that means we have to calculate the combinations of 7 items out of 10 without repetition :
C(10, 7) = 10! / (7! × (10-7)!) = 10! / (7! × 3!) =
= 10×9×8 / (3×2) = 5×3×8 = 120
there are 120 possibilities to build the math club.
e) now we pick 4 students out of 10. but as we give them prices based on ranking, the sequence matters (e.g. Nacy first, Paul second is different to Paul first, Nancy second).
but we still have no repetition, as nobody can win more than one price.
that means we need to calculate the permutations of 4 items out of 10 without repetition :
P(10, 4) = 10! / (10-4)! = 10! / 6! = 10×9×8×7 = 5,040
there are 5040 different ways to distribute the 4 prices among the 10 students.
There are four students running for Class President. On election day,
Samantha got just 6.5% of votes. If there are 277 tallied votes, how many votes
did Samantha get? Round your answer to the nearest whole vote.
Answers
Step-by-step explanation:
6.5%÷100×277
=13×277÷20
=180.05
=180
50 PTS. Solve the given equation by completing the square.
r2 + 8 = 38
Fill in the values of a, b, and c to complete the solutions.

Answers
Answer:
r = 15
Step-by-step explanation:
That's my answer hope it helps brainliest my answer please that's correct
Answer:
r=15
Step-by-step explanation:
hope it helps you bro
Divide the following complex numbers:
(3+ i) / (2-3i)
O A. - 3 - 1
O B. 1 3 - 1
}
C
9 11
+
13 13
D.
3 11
5
Answers
Answer:
Standard complex form 3/13 + 11/13i
Step-by-step explanation:
not sure if this helps
The dimensions of a rectangular pyramid are shown.
6, feet. 8, feet. 4, feet.
What is the volume of this rectangular pyramid in cubic feet?
Answers
The volume of the rectangular pyramid is 64 cubic feet.
What is a rectangular pyramid?A pyramid with a rectangular base is known as a rectangle pyramid. When viewed from the bottom, this pyramid seems to be a rectangle. As a result, the base has two equal parallel sides.
The apex, which is located at the summit of the pyramid's base, serves as its crown. Right or oblique pyramids can be seen in rectangular shapes. If it is a right rectangular pyramid, the peak will be directly over the base's center; if it is an oblique rectangular pyramid, the apex will be angled away from the base's center.
The volume of a rectangular pyramid is given as:
V = (l)(b)(h) / 3
V = (6)(8)(4) / 3
V = 192 / 3
V = 64 cubic feet.
Hence, the volume of the rectangular pyramid is 64 cubic feet.
Learn more about volume here:
https://brainly.com/question/1578538
#SPJ1
The correct question is:

64° 42 °
xº
48°
Find the value of x
Answers
Discuss measures that can be taken to develop the spirit of hard work
The value of log 3 5 × log 25 9 is
Answers
The value of \(log_35 \times log_{25}9\) is 1.
What is an expression?An expression is a way of writing a statement with more than two variables or numbers with operations such as addition, subtraction, multiplication, and division.
Example: 2 + 3x + 4y = 7 is an expression.
We have,
\(log_35 \times log_{25}9\)
\(log_ab = \frac{logb}{loga}\)
So,
= log 5 / log 3 x log 9 / log 25
= log 5 / log 3 x log 3² / log 5²
\(logm^n = n~logm\)
So,
= log 5 / log 3 x log 3² / log 5²
= (log 5 / log 3) x (2 log 3 / 2 log 5)
= (log 5 / log 3) x (log 3 / log 5)
= 1
Thus,
1 is the value.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
Consider the following question.
"Do you watch television every day?"
Which of the following statements BEST explains why the question is NOT a statistical question?
A The question does not anticipate variability in the answers
B The question results in a single absolute answer.
C The question may be answered differently by different people.
D. The question does not require an explanation
Answers
Answer:
a
Step-by-step explanation:
Answer:
C, the only info for the question is about yourself which is a survery question
Step-by-step explanation:
Draw an angle in standard position with the given measure. 8/3 π
Answers
The asterisk (*) represents the vertex of the angle, the initial side is the positive x-axis, and the terminal side is the red line segment that forms an angle of 8/3 π with the positive x-axis.
What is the standard position of angles?
Standard position simply means that the vertex of the angle is at the origin of the circle and that one ray of the angle is on the positive x-axis. The other ray of the angle is placed at the angle measure formed by traveling counter-clockwise along the circle.
To draw an angle in standard position with measure 8/3 π, follow these steps:
Start with the positive x-axis.
Counterclockwise, rotate the initial side of the angle until it coincides with the positive x-axis.
Starting from the initial side on the positive x-axis, rotate the terminal side of the angle in a counterclockwise direction until the angle measures 8/3 π.
The resulting angle will have a measure of 8/3 π and will look like the following:
|
|
--------*-----------
|
|
Here, the asterisk (*) represents the vertex of the angle, the initial side is the positive x-axis, and the terminal side is the red line segment that forms an angle of 8/3 π with the positive x-axis.
To learn more about the standard position of angles visit:
https://brainly.com/question/19882727
#SPJ1
Margie makes a necklace using 14 purple beads for every 6 silver beads. The necklace contains 80 beads. How many of each color bead are in the necklace?
Answers
The quantity of each colour beads that are in the necklace include the following:
Purple beads = 56
Purple beads = 56silver beads = 24
Purple beads = 56silver beads = 24What is a ratio?A ratio is defined as the mathematical expression that shows the number of times one value is contained in another value.
The number of purple beads = 14
The number of silver beads ,= 6
The total quantity of beads = 80
Therefore the total combination = 14+6 = 20
For purple beads = 14/20 × 80/1
= 1120/20 = 56
For silver beads = 6/20×80/1
= 480/20= 24
Learn more about ratio here:
https://brainly.com/question/25927869
#SPJ1
in a survey 420 U.S. females ages 18 to 64, 279 say they have gone to the dentist in the past year. Construct a 90% confidence interval for the population proportion.

Answers
The formula to calculate the confidence interval is
\(P\pm z\times\sqrt[]{\frac{P(1-P)}{n}}\)Where
\(\begin{gathered} P=\text{ sample proportion} \\ n=sample\text{ size} \\ z=\text{ z-score} \end{gathered}\)We can calculate the sample proportion by
\(\begin{gathered} P=\frac{x}{n} \\ \text{Where x is the successes} \end{gathered}\)The parameters are
\(\begin{gathered} x=279 \\ n=420 \\ \end{gathered}\)Using an online calculator, the z-score for a 90% confidence interval is 1.645.
Therefore, we can calculate P to be:
\(P=\frac{279}{420}=0.6643\)Hence, we can calculate calculate the confidence interval by substituting the values
\(\begin{gathered} =0.6643\pm1.645\sqrt[]{\frac{0.6643(1-0.6643)}{420}} \\ =0.6643\pm1.645(0.023) \\ =0.6643\pm0.0378 \end{gathered}\)Therefore, the lower limit of the confidence interval is
\(\begin{gathered} =1.645-0.0378 \\ =1.6072 \end{gathered}\)The lower limit of the confidence interval is 1.6072
Therefore, the upper limit of the confidence interval is
\(\begin{gathered} =1.645+0.0378 \\ =1.6828 \end{gathered}\)Therefore, the upper limit of the confidence interval is 1.6828
A student ran a distance of 3 1/2miles each day for 5 days. Then the student ran a distance of 4 1/4 miles each day for the next 5 days. What was the total distance in miles the student ran during these 10 days?
Answers
Answer:
To find the total distance, we need to add up the distance the student ran in the first 5 days and the distance the student ran in the next 5 days.
Distance for the first 5 days = 3 1/2 miles/day × 5 days = 17.5 miles
Distance for the next 5 days = 4 1/4 miles/day × 5 days = 21.25 miles
Total distance = Distance for the first 5 days + Distance for the next 5 days
Total distance = 17.5 miles + 21.25 miles
Total distance = 38.75 miles
Therefore, the student ran a total of 38.75 miles during these 10 days.
Work out the value of x+y multiplied by z if x=3/5 ....

Answers
Answer:
1.056
Step-by-step explanation:
Because 2 4/5+ 3/5= 3 1/5
3 1/5 as a decimal is, 3.2
3.2× .33= 1.056
What is the constant rate of change for the relationship shown in the table?

Answers
Answer:
3
Step-by-step explanation:
Answer:
3
Step-by-step explanation: