A line has a slope of -1 and passes through the point (-19, 17). Write its equation in slope- intercept form. Write your answer using integers, proper fractions, and improper fractions in simplest form.
Answers
\((\stackrel{x_1}{-19}~,~\stackrel{y_1}{17})\hspace{10em} \stackrel{slope}{m} ~=~ - 1 \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{17}=\stackrel{m}{- 1}(x-\stackrel{x_1}{(-19)}) \implies y -17= -1 (x +19) \\\\\\ y-17=-x-19\implies {\Large \begin{array}{llll} y=-x-2 \end{array}}\)
Related Questions
If the terms of a polynomial do not have a GCF, does that mean it is not factorable?
Answers
can someone please help I pay £100

Answers
Answer:
The new points to the triangle will be:
\(A(1,4)\\ B(1,1)\\ C(-1,1)\)
Step-by-step explanation:
Because the reflection point is at \(x=2\), all x values will subtract their distances from \(x=2\) to get their new values. The y values remain the same.
The starting values are:
\(A(3,4)\\ B(3,1)\\ C(5 ,1)\)
Point \(A\) is 1 unit away from \(x=2\), so we'll subtract 1 from 2 to get the new x value: \(2 - 1 = 1\), so \(A(1,4)\).
Point \(B\) is also 1 unit away from \(x=2\), so we'll subtract 1 from 2 to get the new x value: \(2 - 1 = 1\), so \(B(1,1)\).
Point \(C\) is 3 units away from \(x=2\), so we'll subtract 3 from 2 to get the new x value: \(2 - 3 = -1\), so \(C(-1,1)\).
Calculus please help me

Answers
(1) f(x) = (1 - x³) / (x - 1)
(a) The domain is the set of values that this function can take on. If x = 1, the denominator becomes 0 and the function is undefined. Any other value of x is okay, though, since for x ≠ 1, we have
f(x) = (1 - x³) / (x - 1) = - (1 - x³) / (1 - x) = -(x² + x + 1)
which is defined for all x. This also tells us that the plot of f(x) is a parabola with a hole at x = 1. So, the domain is the interval (-∞, 1) ∪ (1, ∞).
(b) The range is the set of values that the function actually does take on. Taking the simplified version of f(x), we can complete the square to write
-(x² + x + 1) = -(x² + x + 1/4 - 1/4) - 1 = -(x + 1/2)² - 3/4
which is represented by a parabola that opens downward, with a maximum value of -3/4. So the range is the interval (-∞, -3/4).
(c) Judging by the plot of f, the limits at both negative and positive infinity are -∞.
(d) Same answer as part (a).
(2) f(x) = x³ - x
(a) The derivative of f at x = 3, and hence the slope of the tangent line to this point, is
\(f'(3)=\displaystyle\lim_{h\to0}\frac{f(3+h)-f(3)}h\)
\(f'(3)\displaystyle=\lim_{h\to0}\frac{((3+h)^3-(3+h))-24}h\)
\(f'(3)=\displaystyle\lim_{h\to0}\frac{(27+27h+9h^2+h^3)-(3+h)-24}h\)
\(f'(3)=\displaystyle\lim_{h\to0}\frac{26h+9h^2+h^3}h\)
\(f'(3)=\displaystyle\lim_{h\to0}(26+9h+h^2)=\boxed{26}\)
(b) The tangent line at x = 3 has equation
y - f (3) = f ' (3) (x - 3)
y - 24 = 26 (x - 3)
y = 26 x - 54
We also want to find any other tangent lines parallel to this one, which requires finding all x for which f '(x) = 26. We could use the same limit definition as in part (a), but to save time, we exploit the power rule to get
f '(x) = 3 x² - 1
Then solve for when this is equal to 26:
3 x² - 1 = 26 ==> x² = 9 ==> x = ±3
The other tangent line occurs at x = -3, for which we have f (-3) = -24, and so the equation for the tangent is
y - f (-3) = 26 (x - (-3))
y + 24 = 26 (x + 3)
y = 26 x + 54
O dreaptă (d) și punctele A,B și C în aceasta ordine stind ca AB=10cm; BC=14cm desemnați lungimea segmentului [AC]=? Vă rogg dau coroana!!!!la cine e corect
Answers
Answer:
Length of line AC = 24 cm
Step-by-step explanation:
Given:
Length of line AB = 10 cm
Length of line BC = 14 cm
Find:
Length of line AC
Computation:
We know that line AB and BC are two part of line AC
So,
AC = AB + BC
Length of line AC = Length of line AB + Length of line BC
Length of line AC = 10 + 14
Length of line AC = 24 cm
A drama club is planning a bus trip to New York City to see a Broadway play. The cost per person for the bus rental varies inversely to the number of people going on the trip. It will cost $30 per person if 44 people go on the trip. How much will it cost per person if 20 people go on the trip? Round your answer to the nearest cent, if necessary.
Answers
Statement Problem: A drama club is planning a bus trip to New York City to see a Broadway play. The cost per person for the bus rental varies inversely to the number of people going on the trip. It will cost $30 per person if 44 people go on the trip. How much will it cost per person if 20 people go on the trip?
Solution:
Let the cost per person for the bus rental be c;
Let the number of people going on the trip be n;
\(c\propto\frac{1}{n}\)\(\begin{gathered} c=\frac{k}{n} \\ \text{Where k is the constant of proportionality;} \\ k=cn \\ c=30,n=44 \\ k=30\times44 \\ k=1320 \end{gathered}\)Then, we have;
\(\begin{gathered} \text{When;} \\ n=20,c=\text{?} \\ c=\frac{k}{n} \\ c=\frac{1320}{20} \\ c=66.00 \end{gathered}\)If 20 people go on the trip, the cost per person is;
\(\text{ \$66.00}\)A professor tells a student that he has a 90% chance of getting an A for the course that he score an 85 or better on the midterm exam. The student thinks he has only a 50% chance of getting 85 better. what is the probability that the student scores an 85 or better and he receive an A in the score?
Answers
The probability that the student scores an 85 or better and he receive an A in the score is 0.45.
In the question it is given that the professor tells that the student has 90% chance of getting A, if he gets 85 or better in mid term exam.
The student is 50% sure that he will get 85 or better in the examination.
To get the probability of the student scores an 85 or better and he receives an A grade, we use multiplication rule.
P( student getting A grade and 85 or better)= P(getting A) x P(getting 85 or better)
P(getting A)=0.9
P(getting 85 or better)=0.5
= 0.9x0.5
P( student getting A grade and 85 or better)=0.45
Therefore, probability that the student scores an 85 or better and getting A is 0.45.
To know more about probability here:
https://brainly.com/question/11034287#
#SPJ1
Evaluate the expression. Drag the answer into the box to match the expression. 27•((3^3)^-1) a. 27 b.3 c.1 D.1/9 100 POINTS help 100!
Answers
Answer:
\(\Huge \boxed{\mathrm{C. \ 1}}\)
\(\rule[225]{225}{2}\)
Step-by-step explanation:
\(27 \cdot ((3^3)^{-1})\)
Multiplying exponents.
\(27 \cdot 3^{-3}\)
Rewriting 27 with base 3.
\(3^3 \cdot 3^{-3}\)
Adding exponents since bases are the same.
\(3^0 =1\)
\(\rule[225]{225}{2}\)
Answer:
C. 1
Step-by-step explanation:
27 * {(3³)⁻¹}
= 27
3³
= 27
27
= 1
URGENT!! ILL GIVE
BRAINLIEST! AND 100 POINTS

Answers
Answer:
Option is the the. correct answer A
Indicated operation? Perform it?

Answers
98
First you do the exponents.
11^2 = 121
-3^3 = -27
2^2 = 4
So now we have 121 - 27 + 4
And you just go left to right now
121 - 27 = 94
94 + 4 = 98
So the answer is
98
Hope this helps
A mathematical model is a simplified description of a system or a process. In your opinion, how are mathematical models helpful? What are the advantages and disadvantages of using a model? In what ways are mathematical models linked to the fields of chemistry, biology, and physics? Cite several examples.
Answers
Given statement solution is :- Mathematical models are extremely valuable tools in various fields, including chemistry, biology, and physics. They offer several advantages: Simplification and abstraction, Prediction and simulation, Cost and time efficiency, Insight and understanding.
Mathematical models are extremely valuable tools in various fields, including chemistry, biology, and physics. They offer several advantages:
Simplification and abstraction: Mathematical models allow complex systems or processes to be represented using simplified mathematical equations or algorithms. This simplification helps in understanding the underlying principles and relationships of the system, making it easier to analyze and predict outcomes.
Prediction and simulation: Models enable scientists to make predictions about the behavior of a system under different conditions. They can simulate scenarios that are difficult or impossible to observe in the real world, allowing researchers to explore various hypotheses and make informed decisions.
Cost and time efficiency: Models can be used to explore different scenarios and test hypotheses in a relatively quick and cost-effective manner compared to conducting real-world experiments. They can help guide experimental design by providing insights into the most relevant variables and parameters.
Insight and understanding: Mathematical models often reveal underlying patterns and relationships that may not be immediately apparent from experimental data alone. They provide a framework for organizing and interpreting data, leading to a deeper understanding of the system being studied.
However, mathematical models also have limitations and potential disadvantages:
Simplifying assumptions: Models are based on assumptions and simplifications, which may not fully capture the complexity of the real-world system. If these assumptions are incorrect or oversimplified, the model's predictions may be inaccurate or misleading.
Uncertainty and error: Models are subject to uncertainties and errors stemming from the inherent variability of the system, limitations in data availability or quality, and simplifying assumptions. It is crucial to assess and communicate the uncertainties associated with model predictions.
Validation and verification: Models need to be validated and verified against experimental data to ensure their accuracy and reliability. This process requires rigorous testing and comparison to real-world observations, which can be challenging and time-consuming.
Mathematical models are closely linked to the fields of chemistry, biology, and physics, providing valuable insights and predictions in these disciplines. Here are some examples:
Chemistry: Mathematical models are used to study chemical reactions, reaction kinetics, and molecular dynamics. One example is the use of rate equations to model the kinetics of a chemical reaction, such as the reaction between reactants A and B to form product C.
Biology: Mathematical models play a crucial role in understanding biological systems, such as population dynamics, gene regulation, and the spread of infectious diseases. For instance, epidemiological models like the SIR (Susceptible-Infectious-Recovered) model are used to simulate and predict the spread of diseases within a population.
Physics: Mathematical models are fundamental in physics to describe physical phenomena and predict outcomes. One well-known example is Newton's laws of motion, which can be mathematically modeled to predict the motion of objects under the influence of forces.
Quantum mechanics: Mathematical models, such as Schrödinger's equation, are used to describe the behavior of particles at the quantum level, providing insights into atomic and molecular structures and the behavior of subatomic particles.
Fluid dynamics: Mathematical models, such as the Navier-Stokes equations, are employed to study the behavior of fluids, including airflow, water flow, and weather patterns.
These examples demonstrate the wide range of applications for mathematical models in understanding, predicting, and simulating various phenomena in the fields of chemistry, biology, and physics.
For such more questions on Advantages of Mathematical Models
https://brainly.com/question/12653211
#SPJ8
Find the first three powers, A, A2, and A3, of the transition matrix below. Find the probability that state 1 changes to state 2 after three repetitions of the experiment. 0.3 0.1 0.6 A0.5 0.2 0.3 Type an integer or decimal for each matrix element.)
Answers
The probability that state 1 changes to state 2 after three repetitions of the experiment is 0.052.
The first power of the transition matrix A is simply the matrix itself:
A1 = [ 0.3 0.1 0.6 ]
[ 0.5 0.2 0.3 ]
The second power of the transition matrix is obtained by multiplying A by itself:
A2 = A1 * A1 = [ 0.30.3+0.10.5 0.30.1+0.10.2 0.30.6+0.10.3 ]
[ 0.50.3+0.20.5 0.50.1+0.20.2 0.50.6+0.20.3 ]
= [ 0.19 0.06 0.33 ]
[ 0.29 0.08 0.33 ]
The third power of the transition matrix is obtained by multiplying A2 by A:
A3 = A2 * A = [ 0.190.3+0.060.5 0.190.1+0.060.2 0.190.6+0.060.3 ]
[ 0.290.3+0.080.5 0.290.1+0.080.2 0.290.6+0.080.3 ]
= [ 0.161 0.052 0.327 ]
[ 0.247 0.068 0.327 ]
To find the probability that state 1 changes to state 2 after three repetitions of the experiment, we need to look at the second element of the first row of A3. This element is 0.052, so the probability that state 1 changes to state 2 after three repetitions of the experiment is 0.052.
To know more about probability visit :
brainly.com/question/30034780?referrer=searchResults
#SPJ4
Which shows the factored form of the expression below? 100-p^16 (show all steps you took to get to answer)
Answers
Answer:
\(100-p^{16}=(10-p^{8})(10+p^{8})\)
Step-by-step explanation:
Factoring
Binomial factoring is a common task when solving a great variety of math problems.
One of the best-known formula that helps us to factor a binomial is:
\((a^2-b^2)=(a-b)(a+b)\)
It can easily be identified because the expression is the difference between two perfect squares.
The expression
\(100-p^{16}\)
can be factored with the formula above since it's the difference of two squares:
\(a=\sqrt{100}=10\)
\(b=\sqrt{p^{16}}=p^{8}\)
The expression is factored as follows:
\(\boxed{100-p^{16}=(10-p^{8})(10+p^{8})}\)
The Pappas family has two cats, Zeus and Athena. Together they weigh nine pounds. Zeus weighs 3 pounds less than Athena. How much does Athena weigh?
Answers
Answer:
Athena weighs 6 pounds. (Zeus weighs 3 pounds).
Step-by-step explanation:
We know that A (Athena) + Z (Zeus) = 9. And we know that Zeus weighs three pounds less than Athena. Knowing this we can do
1 + 8 = 9
2 + 7 = 9
3 + 6 = 9
We can see that 6 and 3 equal 9 and 6 is 3 away from 3, getting us the answer that Athena weighs 6 pounds. :) I hope this helps! ^^
2X -3 = 9
2X = 12
X = 6
X-3 = ?
6-3 = 3
One cat weighs 6 lbs and one weighs 3 lbs for total of 9 lbs. Athena weighs 6 lbs.
What is the largest five-digit multiple of 15 whose digits are all distinct and nonzero?
Answers
The largest five-digit multiple of 15 whose digits are all distinct and nonzero is 12345.
How can we express numbers belonging to decimal numeral system?Suppose that the number is abcd.efg and belongs to the decimal numerical system. Remember one thing that the place on the left of decimal point is called ones. Move one-one places to right, and divide by 10 and 10 more and more. Move one-one places to left, and multiply (un-divide) by 10 and 10 more and more. We will call d as ones digit, c as tens digit (it get multiplied by 10), b as hundreds digit etc.
WE need to find the five-digit multiple of 15 whose digits are all distinct and nonzero.
Thus, we can see that the largest five-digit multiple of 15 could be ;
12345
Since it must be all distinct and nonzero. so the correct digit is 12345.
Hence, the largest five-digit multiple of 15 whose digits are all distinct and nonzero is 12345.
Learn more about place value here:
https://brainly.com/question/17983725
#SPJ1
Which of the following z-scores is NOT outside the middle 68% of the data for a normal distribution?
a.) -0.8
b.) -2.8
c.) 1.8
d.) 3.8
Answers
Answer:
Step-by-step explanation:
A, use three_digite rounding arithmetic to compute 13- 6 and determine the absolute,relative ,and percentage errors.
tepeat part (b) using three – digit chopping arithmetic.
What is the fraction of 41.66667
Answers
Answer:
\(41\frac{2}{3}\)
I hope this helps!
Answer:
41.66 repeating or 41.67
Step-by-step explanation: hope this helps
Hpw does the graph of the function g (x) =5x +1 differ from the graph of f(x) = 5x
Answers
Answer:
g(x) has a +1 for it's b in y = mx+b, and f(x) has 0 for it's b (b is the y intercept)
Step-by-step explanation:
Bookwork code: N84
This is a new version of the question Make sure you start now workings
Calculate the range, in centimetres (cm), of the following
lengths:
15 cm, 0.5 cm, 10.3 cm, 16.7 cm, 21 cm,
8.6 cm
Answers
The range, in centimetres (cm), of the following lengths is 20.5 cm
What is the range?
The difference between the lowest and highest numbers is referred to as the range. For instance, the range will be 10 - 2 = 8 if the given data set is 2, 5, 8, 10, and 3.
As a result, the range may alternatively be thought of as the distance between the highest and lowest observation. The range of observation is the name given to the outcome. Statistics' range reflects the variety of observations.
Given, 15 cm, 0.5 cm, 10.3 cm, 16.7 cm, 21 cm, 8.6 cm
So, the highest value of length = 21 cm
the lowest value of length = 0.5 cm
Then, range = the highest value - the lowest value
= 21 - 0.5 = 20.5 cm
Hence, the range, in centimetres (cm), of the following lengths is 20.5 cm
To learn more about range
https://brainly.com/question/29794774
#SPJ1
3 5/12 + 1 3/8
WAT IS IT
Answers
Answer:
4 19/24
Step-by-step explanation:
3 5/12 + 1 3/8
denominators multiplied by 3 and the numerators
= 3 10/24 + 1 9/24=4 19/24
Need help on 3b, 4a, 4b
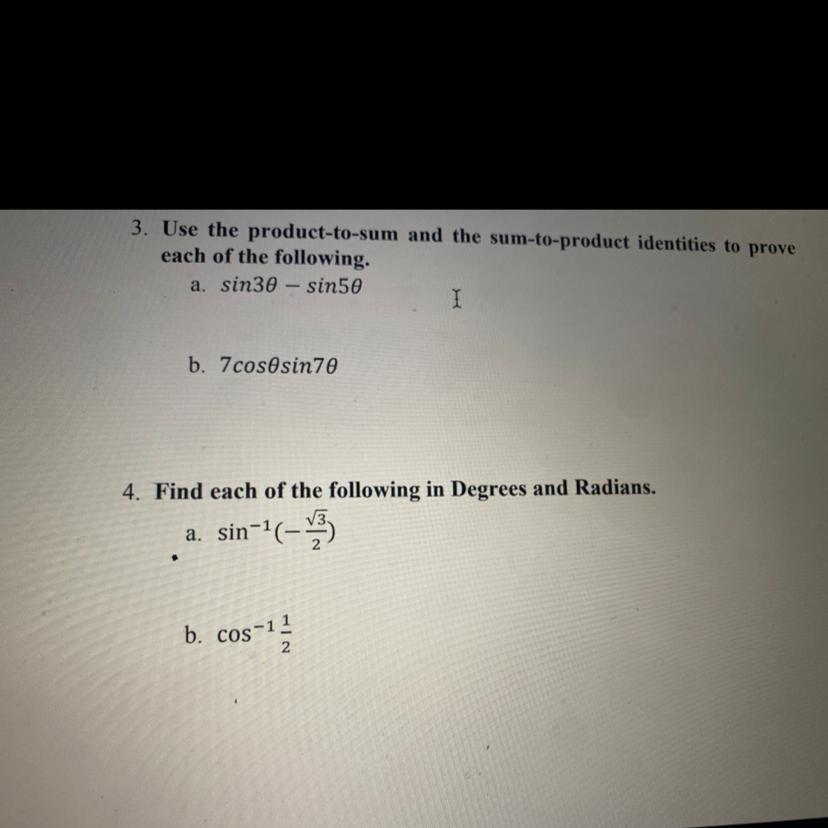
Answers
The values of the given trigonometric functions are 240° and 60° respectively.
What are trigonometric functions?
Trigonometric functions are mathematical functions that relate the angles and sides of a right triangle.
The three primary trigonometric functions are sine, cosine, and tangent.
The sine function (sin) relates the length of the opposite side of an angle to the length of the hypotenuse of a right triangle. It is defined as sin(θ) = opposite/hypotenuse.
The cosine function (cos) relates the length of the adjacent side of an angle to the length of the hypotenuse of a right triangle. It is defined as cos(θ) = adjacent/hypotenuse.
The tangent function (tan) relates the length of the opposite side of an angle to the length of the adjacent side of a right triangle.
Now To find
(a.) sin⁻¹(-√3/2)
(b.) cos⁻¹ (1/2)
For a
sin⁻¹(-√3/2)=sin⁻¹(-0.8660)=-⁻60° or 240°
and
For b
cos⁻¹ (1/2)=cos⁻¹ (0.5)=60°
Hence,
the values of the given trigonometric functions are 240° and 60° respectively.
To know more about Trigonometric functions visit the link
brainly.com/question/9880303
#SPJ9
A company is making concrete blocks. The blocks are in the form of right trapezoidal prisms and have the dimensions shown. What is the volume of one block? Show your work
Please help I give 40 brainly

Answers
Answer:
9180 (cm³)
Step-by-step explanation:
area of cross-section (trapezium) = 0.5 X (12 + 22) X 9
= 0.5 X 34 X 9 = 153 cm²
then multiply that by the length (60)
153 X 60 = 9180 (cm³)
What is cos(tan^-1(-2/3))=
Answers
cos(tan^(-1)(-2/3)) simplifies to 3√13 / 13.
To evaluate the expression cos(tan^(-1)(-2/3)), we can use the trigonometric identity:
cos(tan^(-1)(x)) = 1 / √(1 + x^2)
In this case, x is -2/3. Substituting the value into the identity:
cos(tan^(-1)(-2/3)) = 1 / √(1 + (-2/3)^2)
Now, let's calculate the value:
cos(tan^(-1)(-2/3)) = 1 / √(1 + 4/9)
= 1 / √(13/9)
= 1 / (√13/3)
= 3 / √13
= 3√13 / 13
For more such quaetions on simplifies
https://brainly.com/question/29369267
#SPJ8
Help help help help math

Answers
6x+18

The repeated-measures ANOVA is a two-stage process. Which statement accurately describes the second stage of this process
Answers
The statement that describes the second stage of the repeated-measures ANOVA is: it removes individual differences from the denominator.
The repeated-measures ANOVA is a two stage process that is described as analysis of dependencies. This test is used to prove an assumed cause-effect relationship between varaibles (dependent and independent).
The means across one or more variables which have repeated observations are compared using the repeated-measures ANOVA.
Total variability is divided into variability between and within treatments in the first stage of the repeated-measures ANOVA, while the second stage removes individual differences from the denominator.Learn more about the repeated-measures ANOVA on:
https://brainly.com/question/15394749
A piece of lumber 2.8 meters long weighs 24.5 kilograms. A piece 0.8 meter long is cut from
the 2.8-meter length. Determine the weight of the 0.8-meter piece.
Answers
The weight of the 0.8-meter piece is 19.6 kilograms.
We can use the ratio of length to weight to determine the weight of the 0.8-meter piece.
Let's call the weight of the 2.8-meter piece "W₁" and the weight of the 0.8-meter piece "W₂". Then we have:
W₁/2.8m = 24.5kg/1m
Solving for W₁, we get:
W₁ = (24.5kg/1m) x 2.8m = 68.6kg
Now we can use the same ratio to find W₂:
W₂/0.8m = 24.5kg/1m
Solving for W₂, we get:
W₂ = (24.5kg/1m) x 0.8m = 19.6kg
Therefore, the weight of the 0.8-meter piece is 19.6 kilograms.
To learn more on Ratios click:
https://brainly.com/question/1504221
#SPJ1
Hatif has $150 in his account. He saves $80 each month. How long will it take before he has $630 in his account?
Answers
Answer:
6 months
Step-by-step explanation:
We can set up an equation based on his monthly savings to find out how long it will take for Hatif to reach $630 in his account.
Let's assume it takes Hatif "n" months to reach $630 in his account. Each month, he saves $80.
The equation representing the situation is:
$150 + $80n = $630
Now, let's solve for "n":
$80n = $630 - $150
$80n = $480
n = $480 / $80
n = 6
Therefore, it will take Hatif 6 months to reach $630 in his account.
Graph the line 4x+y= 8
Answers
Y-intercept is (0,8)
Mrs. Smith baked 2 cakes. There are seven people in her family. How much of the cakes can each person have? Make sure to write your answer as a simplified fraction.
Answers
The required, each person can have 2/7 of a cake. This fraction cannot be simplified any further, so the answer is 2/7.
What is the fraction?A fraction is a mathematical concept that can be used to express a portion of a whole or a number that can be written as the ratio of two integers.
here,
To divide the 2 cakes equally among 7 people, we can use division. We can think of the total amount of cake as 2 whole cakes or 2/1 cakes. To find out how much cake each person can have, we can divide the total amount of cake by the number of people:
2/1 cakes ÷ 7 people = 2/1 × 1/7 = 2/7 cakes per person
So each person can have 2/7 of a cake. This fraction cannot be simplified any further, so the answer is 2/7.
Learn more about fractions here:
https://brainly.com/question/30193711
#SPJ9
Which negative angle is equivalent to 275°?
O A. -75°
OB. -65°
O C. -95°
OD. -85
Answers
Answer:
-85º
Step-by-step explanation:
275 - 360 = -85
In each diagram, line f is parallel to line g, and line t intersects lines f and g
Answers
In each diagram, line f is parallel to line g, and line t intersects both lines f and g. The given information suggests the application of certain geometric properties and relationships.
Firstly, when a transversal line (line t) intersects two parallel lines (lines f and g), it creates several pairs of corresponding angles.
Corresponding angles are congruent, meaning they have equal measures. This property can be used to determine the measures of specific angles in the diagram.
Secondly, when a transversal intersects parallel lines, it also creates alternate interior angles and alternate exterior angles.
Alternate interior angles are congruent, as well as alternate exterior angles.
By utilizing these properties and relationships, one can analyze the diagram and determine the measures of various angles.
It is important to measure angles systematically and compare them to find congruent or equal measures.
For more such questions on geometric properties
https://brainly.com/question/23949211
#SPJ8