A hotel housekeeper has cleaned
1/3

of the first floor in
1/5
of an hour. At what rate is she cleaning?

Answer:

the range for this problem is the first one

The range of  f(x) =(3/4)ˣ- 4 function is {yly>-4}, Option A is correct.

A relation is a function if it has only One y-value for each x-value.

The function f(x) = (3/4)ˣ- 4 is an exponential function with a base of 3/4. The base is between 0 and 1, which means that the function is decreasing as x increases.

The function has a vertical asymptote at x = infinity, since the base is between 0 and 1, and the function approaches 0 as x approaches negative infinity.

As the exponential function (3/4)ˣ approaches 0 as x approaches infinity, we have:

lim((3/4)ˣ) = 0 as x -> infinity

So, the range of the given function is all real numbers greater than -4.

Hence, the range of function f(x) =(3/4)ˣ- 4  is {yly>-4}, Option A is correct.

To learn more on Functions click:

https://brainly.com/question/30721594

#SPJ7

The results of operations between vectors are, respectively:

Case A: u + w = <- 3, - 1>

Case B: - 6 · v = <6, 6>

Case C: 3 · v - 6 · w = <- 21, - 15>

Case D: 4 · w + 3 · v - 5 · u = <39, 4>

Case E: |w - v| = √(4² + 3²) = 5

In this problem we must determine the operations between vectors, this can be done by following definitions:

Vector addition

v + u = (x, y) + (x', y') = (x + x', y + y')

Scalar multiplication

α · v = α · (x, y) = (α · x, α · y)

Norm of a vector

|u| = √(x² + y²)

Now we proceed to determine the result of each operation:

Case A:

u + w = <- 6, - 3> + <3, 2>

u + w = <- 3, - 1>

Case B:

- 6 · v = - 6 · <- 1, - 1>

- 6 · v = <6, 6>

Case C:

3 · v - 6 · w = 3 · <- 1, - 1> - 6 · <3, 2>

3 · v - 6 · w = <- 3, - 3> + <- 18, - 12>

3 · v - 6 · w = <- 21, - 15>

Case D:

4 · w + 3 · v - 5 · u = 4 · <3, - 2> + 3 · <- 1, - 1> - 5 · <- 6, - 3>

4 · w + 3 · v - 5 · u = <12, - 8> + <- 3, - 3> + <30, 15>

4 · w + 3 · v - 5 · u = <39, 4>

Case E:

|w - v| = |<3, 2> - <- 1, - 1>|

|w - v| = |<4, 3>|

|w - v| = √(4² + 3²) = 5

To learn more on vectors: https://brainly.com/question/31900604

#SPJ1

Answer:

490000

Step-by-step explanation:

Substituting \(x=40\),

\(I=-425(40)^2 + 45500(40) - 650000=490000\)

Answer:

He omitted the value "6" from the input value and added it to the output values. Also, he omitted the value "12" as an output value.

Step-by-step explanation:

Bobby didn't map the relation well. He omitted "6" which is supposed to be an input value and rather included it among the output values (y-values).

"12" was omitted also under output values.

All of these make the the relation not to be a function anymore.

If Bobby had mapped the relation well, the ordered pair would have obviously been a function as every x-value will have exactly one y-value assigned the it.

Answer:

x = -8 1/3

Step-by-step explanation:

Area of rectangular prism: Base x Height.

so 3x1/3x2/5=0.4 0r 2/5

The ratio of oranges to the fruits is 2 : 9 in the simplest form.

We are given that we have:

4 strawberries

3 blueberries

7 bananas

and  4 oranges.

So, the total fruits we have are:

Total fruits = 4 + 3 + 7 + 4

Total fruits = 7 + 11

Total fruits = 18 fruits

Now, we need to find the ratio of oranges in these fruits.

Ratio refers to the representation of one number with respect to the other number.

So, the ratio will be:

Ratio = 4 : 18

Simplifying the ratio, we get that:

Ratio = 2 : 9

Therefore, the ratio of oranges to the fruits is 2 : 9 in the simplest form.

Learn more about ratio here:

https://brainly.com/question/2328454

#SPJ9

Answer: 34,650 permutations

On solving the provided question, by the help of BODMAS we can say that - Subtract 22 from both sides is the answer to the given question.

BODMAS and PEDMAS are both names for it in various places. This stands for exponents, parenthesis, division, multiplication, addition, and subtraction. The BODMAS rule states that parentheses must be answered before powers or roots (that is, of), divisions, multiplications, additions, and lastly subtractions. The BODMAS rule states that the degree (52 = 25), parenthesis (2 + 4 = 6), any division or multiplication (3 x 6 (bracket response) = 18), and any addition or subtraction (18 + 25 = 43) come before any other operations.

\(f/3 +22 = 17\)

\(f/3 +22 -22 = 17 -22\) Subtracting the same value from both sides keeps the equation equal.  

Then simplify. The \(+22 and -22= 0\) They "cancel"   \(17-22 = -5\)

\(f/3 = -17 f/3\) is now isolated-- by itself-- in the equation.

If we have to solve  f, the next step we to take is to multiply on the both sides by  3.

To know more about BODMAS visit:
https://brainly.com/question/29795897

#SPJ1

The estimate of the number of pretzel rolls sold in March will be 890.

The following can be deduced based on the information that given:

March 8-14. 304

March 15-21 271

March 22-28. 316

Therefore, it should be noted that 304 to the nearest ten is 300.

271 to the nearest ten will be 270

316 to the nearest ten will be 320

Therefore, the total number sold in March will be:

= 300 + 270 + 320

= 890

Learn more about numbers on:

brainly.com/question/25734188

#SPJ1

Answer:

B. Cube and E. hexahedron

Step-by-step explanation:

Icosahedron are made of triangles, cubes are made of squares, tetrahedron are made of triangles, octahedron are made of triangles, hexahedron are made of squares, dodecahedron are made of pentagons.

i hope it helps! Have a great day!

Sandra~

Answer:

True

Step-by-step explanation:

If the discriminant \(D=b^2-4ac < 0\), then there are two complex roots

If the discriminant \(D=b^2-4ac > 0\), then there are two real roots

If the discriminant \(D=b^2-4ac=0\), then there is only one real root

Answer: £188

Step-by-step explanation:

Given

The depth of the hole is 80 m

For the first meter, it is £30

After that, it is £2 per meter

after a meter, it is 79 m more

The total cost is C

\(\Rightarrow C=30+2\times 79\\\Rightarrow C=30+158=188\)

Answer: Your welcome!

Step-by-step explanation:

O 1.7278

El porcentaje de error del 16.1% se refiere a la raíz de la ecuación f(x) = x - (√5x - e^x), comenzando en xo = 0.5. Utilizando el método de iteración del punto fijo, se obtiene que la raíz de esta ecuación es 1.7278.

Answer:

Step-by-step explanation:

Para encontrar la raíz de la ecuación f(x) = x - (√(5x) - e^x) con un porcentaje de error del 16.1%, podemos utilizar el método de iteración de punto fijo con la siguiente fórmula:

x1 = f(x0) + x0

Donde x0 es el valor inicial, f(x) es la función y x1 es el siguiente valor de la raíz aproximada.

Primero, evaluamos la función en x0 = 0.5:

f(0.5) = 0.5 - (√(5*0.5) - e^0.5) = -0.2749

Luego, usamos la fórmula para encontrar el siguiente valor:

x1 = f(0.5) + 0.5 = 0.2251

Continuamos iterando hasta que el porcentaje de error sea menor o igual al 16.1%. Podemos calcular el porcentaje de error relativo por iteración con la siguiente fórmula:

Error relativo (%) = |(x_nuevo - x_viejo) / x_nuevo| * 100%

donde x_nuevo es el valor actual de la raíz aproximada y x_viejo es el valor anterior de la raíz aproximada.

Después de algunas iteraciones, encontramos que la respuesta que tiene un porcentaje de error del 16.1% es 1.7351.

Answer:

0-4: Make it 1 unit tall

5-9: Make it 5 units tall

10-14: Make it 4 units tall

15-19: Make it 1 unit tall

20-24: Make it 2 units tall

Step-by-step explanation:

0-4: 3 (1 number)

5-9: 5, 5, 7, 8, 8 (5 numbers)

10-14: 10, 11, 12, 13 (4 numbers)

15-19: 17 (1 number)

20-24: 22, 23 (2 numbers)

Answer:

c. -13/4.

d. -13/3.

Step-by-step explanation:

c. f(3/2) = (1/2)(3/2) - 4

= 3 / 4 - 4

= 0.75 - 4

= -3.25

= -3 and 1/4

= -13/4.

d. f(-2/3) = (1/2)(-2/3) - 4

= -2/6 - 4

= -1/3 - 4

= -1/3 - 12/3

= -13/3.

Hope this helps!

Read more about homeowners insurance

brainly.com/question/30179892

#SPJ1

Answer:

386.75

Step-by-step explanation:

added in the picture

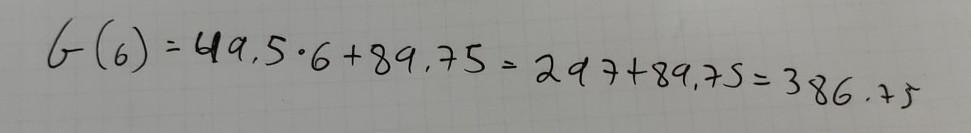
The cost of joining the gym for 6 months is 386.75.

Given,

The function G(m) = 49.5m + 89.75 represents the cost of joining the gym in addition to the one-time membership fee.

The cost, G, is measured in dollars for m months.

We need to find the value of G(6).​

Here,

The one-time membership = 89.75.

Now,

Putting m = 6 months in:

G(m) = 49.5m + 89.75

G(6) = 49.5 x 6 + 89.75

       = 297 + 89.75

       = 386.75

Thus the cost of joining the gym for 6 months is G(6) = 386.75.

Learn more about finding the value of a function here:

https://brainly.com/question/8822000

#SPJ2

B.  y = 0.8x

Hi there !

$38 ............. 100%

$30.4 ...............x%

x = 30.4×100/38 = 3040/100 = 80% = 80/100 = 0.8

y = 0.8x

Good luck !

Answer:

As per the given information there are 4 different price intervals.

Let x be the age and y be the admission price, then we have following equations;

Answer:

\(\mathbf{S =6 \sqrt{1 + \dfrac{\pi^2}{9} }+ \dfrac{18}{\pi} In (\dfrac{\pi}{3}+ \sqrt{1+ \dfrac{\pi^2}{9}})}\)

Step-by-step explanation:

Given that

curve \(y = \dfrac{\pi x}{3}, 0 \leq x \leq 3\)

The objective is to find the area of the surface obtained by rotating the above curve about the x-axis.

Suppose f is positive and posses a continuous derivative,

the surface is gotten by the rotating the curve about the x-axis is:

\(S = \int ^b_a 2 \pi f (x) \sqrt {1 + (f' (x))^2 } \ dx\)

The derivative of the function \(y' = \dfrac{\pi}{3} cos \dfrac{\pi x}{3}\)

As such, the surface area is:

\(S = \int ^3_0 2 \pi sin \dfrac{\pi x}{3} \sqrt {1 +(\dfrac{\pi}{3}cos \dfrac{\pi x}{3})^2 } \ dx\)

Suppose ;

\(u = \dfrac{\pi}{3}cos \dfrac{\pi x}{3}\)

\(du = -( \dfrac{\pi}{3})^2 sin \dfrac{\pi x}{3} \ dx\)

If x = 0 , then \(u = \dfrac{\pi}{3}cos \dfrac{\pi (0)}{3} = \dfrac{\pi}{3}\)

If x = 3 , then \(u = \dfrac{\pi}{3}cos \dfrac{\pi (3)}{3}\)

\(u = \dfrac{\pi}{3}(-1)\)

\(u = -\dfrac{\pi}{3}\)

The equation for S can now be rewritten as:

\(S = \int^3_0 2 \pi sin \dfrac{\pi x}{3} \sqrt{1+(\dfrac{\pi}{3} cos \dfrac{\pi x}{3})^2 }\ dx\)

\(S = 2 \pi \int ^{-\frac{\pi}{3} }_{\frac{\pi}{3}}(-\dfrac{9 \ du }{\pi^2} ) \sqrt{1+u^2}\)

\(S = 18 \pi * \dfrac{1}{\pi ^2 } \int ^{-\frac{\pi}{3}}_{\frac{\pi}{3}} \sqrt{1+u^2} \ du\)

\(S = \dfrac{18} {\pi} \int ^{-\frac{\pi}{3}}_{\frac{\pi}{3}} \sqrt{1+u^2} \ du\)

\(S = \dfrac{18} {\pi} (2 \int ^{-\frac{\pi}{3}}_{0} \sqrt{1+u^2} \ du)\)

since \((\int ^a_{-a} fdx = 2\int^a_0 fdx , f= \sqrt{1+u^2} \ is \ even )\)

Applying the formula:

\(\int {\sqrt{1+x^2}} \ d x= \dfrac{x}{2} \sqrt{1+x^2}+ \dfrac{1}{2} In ( x + \sqrt{1+x^2})\)

\(S = \dfrac{36}{x}[ \dfrac{u}{2} \sqrt{1+u^2}+ \dfrac{1}{2} \ In (u+ \sqrt{1+u^2}) ] ^{\frac{\pi}{3}}_{0}\)

\(S = \dfrac{36}{x}[ \dfrac{\dfrac{\pi}{3}}{2} \sqrt{1+\dfrac{\pi^2}{9}}+ \dfrac{1}{2} \ In (\dfrac{\pi}{3}+ \sqrt{1+\dfrac{\pi^2}{9}})-0 ]\)

\(S =6 \sqrt{1 + \dfrac{\pi^2}{9} }+ \dfrac{18}{\pi} In (\dfrac{\pi}{3}+ \sqrt{1+ \dfrac{\pi^2}{9}})\)

Therefore, the exact area of the surface is \(\mathbf{S =6 \sqrt{1 + \dfrac{\pi^2}{9} }+ \dfrac{18}{\pi} In (\dfrac{\pi}{3}+ \sqrt{1+ \dfrac{\pi^2}{9}})}\)

The area of the surface is,\(S = 6\sqrt{1+\dfrac{\pi ^2}{3}} + \dfrac{18}{3}\ ln (\dfrac{\pi }{3}+\sqrt{1+\dfrac{\pi ^2} {9}})\).

Given that,

The exact area of the surface obtained by rotating the curve about the x-axis. y = sin πx\3 , 0 ≤ x ≤ 3.

We have to determine,

Area of the surface obtained by rotating the curve.

According to the question,

Suppose f is positive and posses a continuous derivative,

The surface is gotten by the rotating the curve about the x-axis is:

Area of the surface is given by,

\(S = \int\limits^b_a {2\pi f(x) .\sqrt{1+ (f'(x))} } \, dx\)

The given curve is x-axis,

\(y = \dfrac{sin\pi x}{3}\)

The derivative of the function is,

\(\dfrac{dy}{dx} =\dfrac{\pi }{3} \dfrac{ cos\pi x}{3}\)

The surface area is,

\(S = \int\limits^b_a {2\pi f(x) .\sqrt{1+(\dfrac{\pi }{3} \dfrac{ cos\pi x}{3})^2} }}} \, dx\)

Substitute the value of f(x),

\(S = \int\limits^3_0{2\pi\dfrac{sin\pi x}{3} .\sqrt{1+(\dfrac{\pi }{3} \dfrac{ cos\pi x}{3})^2} }}} \, dx\)

Suppose;

\(u = \dfrac{\pi }{3}cos\dfrac{\pi x}{3}dx\\\\\du =( \dfrac{-\pi }{3})^2 sin\dfrac{\pi x}{3}dx\\\\if \ x = 0, \ then \ u = \dfrac{\pi }{3}cos\dfrac{\pi (0)}{3} = \dfrac{\pi }{3}\\\\if \ x = 3, \ then \ u = \dfrac{\pi }{3}cos\dfrac{\pi (3)}{3} = \dfrac{\pi }{3}(-1)= \dfrac{-\pi }{3}\)

Then,

\(S = \int\limits^3_0{2\pi\dfrac{sin\pi x}{3} .\sqrt{1+(\dfrac{\pi }{3} \dfrac{ cos\pi x}{3})^2} }}} \, dx\\\\S = 2\pi \int\limits^{\frac{-\pi}{3}}_ \frac{\pi }{3} (\dfrac{-9du}{\pi ^2})\sqrt{1+u^2} \ du\\\\S = 18\pi \times \dfrac{1}{\pi ^2}\int\limits^{\frac{-\pi}{3}}_ \frac{\pi }{3} \sqrt{1+u^2} \ du\\\\S = \dfrac{18}{\pi}\int\limits^{\frac{-\pi}{3}}_ {0} 2\sqrt{1+u^2} \ du\\\\\\\)

Since,

\((\int\limits^a_{-a}{f} \, dx = 2\int\limits^a_0 {f} \, dx , \ f = \sqrt{1+u^2}\ is \ even)\)

By applying the formula to solve the given integration,

\(\int {\sqrt{1+x^2} } \, dx = \dfrac{x}{2}\sqrt{1+x^2} + \dfrac{1}{2} \ ln(x+\sqrt{1+x^2})\\\\S = \dfrac{36}{2} [ \dfrac{u}{2} \sqrt{1+u^2} + \dfrac{1}{2} \ ln(u+\sqrt{1+u^2})}]^{\frac{\pi }{3}}_0\\\\\)

\(S = \dfrac{36}{2} [ \dfrac{\dfrac{\pi }{3}}{2} \sqrt{1+\dfrac{\pi^2 }{9}} + \dfrac{1}{2} \ ln(\dfrac{\pi }{3}+\sqrt{1+\dfrac{\pi ^2} {9}}-0)]\\\\S = 6\sqrt{1+\dfrac{\pi ^2}{3}} + \dfrac{18}{3}\ ln (\dfrac{\pi }{3}+\sqrt{1+\dfrac{\pi ^2} {9}})\)

Hence, The area of the surface is,\(S = 6\sqrt{1+\dfrac{\pi ^2}{3}} + \dfrac{18}{3}\ ln (\dfrac{\pi }{3}+\sqrt{1+\dfrac{\pi ^2} {9}})\)

To know more about Integration click the link given below.

https://brainly.com/question/17256859

The actual annual value of this job to Karla is 33000.

What are arithmetic operations?

Arithmetic operations is a branch of mathematics that studies numbers and the operations on numbers that are useful in all other branches of mathematics. It consists primarily of operations like addition, subtraction, multiplication, and division.

We have,

the job will pay 2400 per month,

if the full cost of the medical insurance is 450 a month and Karla plans to contribute the full 1500 every year tpa retirement plan,

the actual annual value of this job to Karla is:

2400 per month

annual value  = 2400 * 12 = 28,800

the medical insurance is 450 a month

half the cost of medical insurance is  225 a month

annual value  = 225  * 12 = 2700

the full 1500 every year tpa retirement plan,

So, the total value is:

= 28,800 + 2700 + 1500

= 33000

Hence,  the actual annual value of this job to Karla is 33000.

To learn more about arithmetic operations visit,

brainly.com/question/4721701

#SPJ1

Answer:

4

Step-by-step explanation:

because variable is independent

The probabilities, we need to understand the context. Assuming we are working with a fair six-sided die, where each face has an equal chance of landing, here are the probabilities:

For such more questions on probability

https://brainly.com/question/30390037

#SPJ8

The amount of rainfall is an illustration of inverse functions, and rates.

The function is given as: R = f(t)

(a) Interpret f(6) = 4.8

This means that:

The amount of rainfall at 6 seconds is 4.8 cm

(b) Interpret f'(6) = 0.5

f'(6) represents the rate of the function

So, this means that:

The rate at which rain falls at 6 seconds is 0.5 cm per second

(c) Interpret f^-1(5) = 14

f^-1(6) represents the inverse function

So, this means that:

The time at which 5 cm of rain falls, is 14 seconds

(d) Interpret f^-1'(5) = 1.5

f^-1'(5) represents the rate of the inverse function

So, this means that:

The rate of time when 5 cm of rain falls is 1.5 seconds per cm

Read more about functions, inverse and rates at:

https://brainly.com/question/15634149

Answer:

x = 6

Step-by-step explanation:

Vertical angles in a geometry are equal. Hence m<A = m<B

Given that

m<A =  3x - 9

m<B - x+3

Then 3x - 9 = x+3

3x - x = 3 + 9

2x = 12

Divide both sides by 2

2x/12 = 12/2

x = 6

Hence the value of x is 6