A group of friends wants to go to the amusement park. They have no more than $120 to spend on parking and admission. Parking is $12, and tickets cost $13. 50 per person, including tax. Write and solve an inequality which can be used to determine p, the number of people who can go to the amusement park
Answers
The inequality which can be used to determine p, the number of people who can go to the amusement park is 12+13.50p≤120 and the value of p should be less than or equal to 8.
According to the question,
We have the following information:
A group of friends wants to go to the amusement park. They have no more than $120 to spend on parking and admission. Parking is $12, and tickets cost $13. 50 per person, including tax.
And p represents the number of people who can go to the amusement park.
12+13.50p≤120
Subtracting 12 from both sides:
13.50p ≤120-12
13.50p ≤108
Dividing by 13.50 on both sides:
p ≤ 108/13.50
p ≤ 8
Hence, the inequality which can be used to determine p, the number of people who can go to the amusement park is 12+13.50p≤120 and the value of p should be less than or equal to 8.
To know more about inequality here
https://brainly.com/question/28823603
#SPJ4
Related Questions
Help with geometry on equations of circles. What would be the center of the circle and what is the length of the radius of this circle?

Answers
The coordinates of the center is (32, 40.5).
length of the radius of the circle is 73 units.
How to find the center coordinatesThe coordinates of the center is solved using the formula for midpoints expressed as
Midpoint x-coordinate = (x₁ + x₂) / 2
Midpoint y-coordinate = (y₁ + y₂) / 2
Plugging in the values:
x₁ = 8 and y₁ = 13
x₂ = 56 and y₂ =68
Midpoint x-coordinate
= (8 + 56) /2
= 64/2
= 32
Midpoint y-coordinate
= (13 + 68) /2
= 81/ 2
= 40.5
distance formula will be used to find the length of the radius of the circle
d = √[(x₂ - x₁)² + (y₂ - y₁)²]
Plugging in the values:
= √[(56 - 8)² + (68 - 13)²]
= √(48² + 55²)
= √(2304 + 3025)
= √5329
= 73
Learn more about circle at
https://brainly.com/question/24375372
#SPJ1
An oil company purchased an option on land in Alaska. Preliminary geologic studies assigned the following probabilies.
P( high-quality oil )
P( medium-quality oil )
P( no oil )
=0.55
=0.25
=0.20
a. What is the probability of finding oil (to 2 decimals)? P( soil ∣ high-quality oil )=0.25 P( soil ∣ medium-quality oil )=0.70 P( soil ∣ no oil )=0.25 Given the soil found in the test, use Bayes' theorem to compute the following revised probabilities (to 4 decimals). P (high-quality oil|soil) P( medium-quality oil ∣ soil ) P( no oil ∣ soil ) What is the new probability of finding oil (to 4 decimals)? According to the revised probabilities, what is the quality of oil that is most likely to be found?
Answers
The probability of finding oil in Alaska is 0.45. The revised probabilities, obtained using Bayes' theorem, indicate that the most likely quality of oil to be found is medium-quality oil.
To calculate the probability of finding oil, we need to consider the probabilities of finding oil given different qualities. The probability of finding oil can be obtained by summing the individual probabilities of finding oil of high-quality, medium-quality, and no oil.
P(high-quality oil | soil) = P(soil | high-quality oil) * P(high-quality oil) / P(soil)
P(medium-quality oil | soil) = P(soil | medium-quality oil) * P(medium-quality oil) / P(soil)
P(no oil | soil) = P(soil | no oil) * P(no oil) / P(soil)
Given the preliminary geologic studies, P(soil | high-quality oil) = 0.25, P(soil | medium-quality oil) = 0.70, and P(soil | no oil) = 0.25. The probabilities of high-quality oil, medium-quality oil, and no oil are 0.55, 0.25, and 0.20, respectively.
Using Bayes' theorem, we can calculate the revised probabilities:
P(high-quality oil | soil) = (0.25 * 0.55) / (0.25 * 0.55 + 0.70 * 0.25 + 0.25 * 0.20)
P(medium-quality oil | soil) = (0.70 * 0.25) / (0.25 * 0.55 + 0.70 * 0.25 + 0.25 * 0.20)
P(no oil | soil) = (0.25 * 0.20) / (0.25 * 0.55 + 0.70 * 0.25 + 0.25 * 0.20)
After calculating these values, we find that the new probability of finding oil is 0.45. This means that there is a 45% chance of finding oil. According to the revised probabilities, the quality of oil that is most likely to be found is medium-quality oil.
To learn more about probability click here: brainly.com/question/31828911
#SPJ11
select all expressions that are equivalent to 2to the power of 4 / ((3.2 x 0.8) + 1.44)
Answers
The value of the given expression will be 4.
What is an expression?
Expression in maths is defined as the relation of numbers variables and functions by using mathematical signs like addition, subtraction, multiplication and division.
Given that the expression is 2⁴ / ( 3.2 x 0.8 0 + 1.44 ). SOlve the expression as below,
E = 2⁴ / ( 3.2 x 0.8 ) + 1.44 )
Solve the denominator by mathematical operation.
E = 16 / ( 2.56 + 1.44 )
Divide the numerator by denominator,
E = 16 / 4
E = 4
Therefore, the solution of the expression is 4.
To know more about an expression follow
https://brainly.com/question/29194314
#SPJ9
Select the equation that is true.
5,400 ÷ 9 = 4,500 ÷ 5
3,500 ÷ 7 = 2,400 ÷ 3
2,700 ÷ 9 = 4,000 ÷ 8
3,500 ÷ 7 = 4,500 ÷ 9
Answers
Verbal
4. When describing sets of numbers using interval notation, when do you use a parenthesis and when do you use a bracket?
Answers
Step-by-step explanation:
A parenthesis is used when the number next to it is NOT part of the solution set
like : all numbers up to but not including 3 .
Parens are always next to infinity when it is part of the solution set .
A bracket is used when the number next to it is included in the solution set.
If S is a non-empty subset of R^n such that any linear combination of vectors in S is again a vector in S, then S is a subspace of R^n
Answers
Any non-empty subset of Rⁿ, where any linear combination of vectors in S is again a vector in S, is a subspace of Rⁿ.
Given that S is a non-empty subset of Rⁿ such that any linear combination of vectors in S is again a vector in S. Therefore, to prove that S is a subspace of Rⁿ, we have to show that S satisfies three conditions. These conditions are as follows;
The condition for being a subspace of Rⁿ
Firstly, a subspace must be closed under addition. In other words, if x and y are any two vectors in S, then their sum x + y must be in S.
Secondly, a subspace must be closed under scalar multiplication. In other words, if x is any vector in S and c is any scalar, then cx must be in S.
Finally, a subspace must contain the zero vector, denoted by 0.S is a subspace of Rⁿ
From the conditions mentioned above, we can show that S is indeed a subspace of Rⁿ, since S satisfies all the required conditions.
Therefore, we can say that any non-empty subset of Rⁿ, where any linear combination of vectors in S is again a vector in S, is a subspace of Rⁿ.
To know more about subset, click here
https://brainly.com/question/31739353
#SPJ11
(HALP MY LAST EASY QUESTION ILL MARK BRAINLY)

Answers
Answer:
(A) g(0) = 8, this indicates the y-intercept.
(B) the number in the parentheses is less than 1 but more than 0.
(C) sorry
Step-by-step explanation:
(A) plug in 0 for x.
(B) the number in the parentheses is less than 1 but more than 0. This means that it's decreases.
(C) Sorry I can't upload photos.
Which graph represents y as a function of x

Answers
F(x)=x^2. What is g(x)?

Answers
given f(x) and g(x) = k*f(x), use the graph to determine the value of k

Answers
g(x)=k•f(x)
So we can say the following
g(-2)=k•f(-2)
Plugging in the values for g and f we have
-10=2k
Dividing both sides by 2 we get
k=-5
Hope this helps!
The graph shows the area of a rectangle given its length for a rectangle with a perimeter of 120 meters. What dimensions maximizes the area of the rectangle
A 10 m by 60 m
B 20 m by 40 m
C 30 m by 30 m
D 30 m by 90 m
E 60 m by 60 m

Answers
Answer:
ITS C. 30 m by 30 m
Step-by-step explanation:
Claire buys a car for 5700pounds
she pays a deposit of 12%
she then pays the rest of the cost in 15 equal monthly payments.
how much is each monthly payment?
Answers
Answer:
£334.40
Step-by-step explanation:
12% of 5700
= \(\frac{$(12\times 5700)/100$}\)
= 684
= the deposit
5700 - 684 = 5016
this is the amount that needs to be paid after the deposit.
5016 / 15 = 334.40
= £334.40
A calculator requires a keystroke assembly and a logic circuit. Assume that 83% of the keystroke assemblies and 88% of the logic circuits are satisfactory. Assuming that defects in keystroke assemblies are independent of defects in logic circuits, find the probability that a finished calculator will be satisfactory. Group of answer choices
Answers
Answer:
0.7304
Step-by-step explanation:
According to the Question,
Given That, A calculator requires a keystroke assembly and a logic circuit. Assume that 83% of the keystroke assemblies and 88% of the logic circuits are satisfactory.We have,
P(keystroke satisfactory) =0.83 , P(logic satisfactory)= 0.88
Assuming that defects in keystroke assemblies are independent of defects in logic circuitsSince the events are independent. So, the probability that a finished calculator will be satisfactory
⇒ 0.83×0.88
⇒0.7304
4 divided by 2/3
pls pls pls pls pls help pls pls
Answers
Answer:
4 divided by 2/3 (4 ÷ 2/3) = 6
Step-by-step explanation:
When you divide one number by another , this is the same as multiplying that one number by the reciprocal of that other number. So a/b = a × 1/b = a × b^-1.
Also a reciprocal is the same as taking something to the power of -1.
When you take the reciprocal of a fraction, just flip the numerator, and denominator.
b^-1 = 1/b.
b^-n = 1/b^n.
(a/b)^-1 = b/a
a/b^-1 = ab
Therefore 4 / (2/3) = 4 × 3/2 = 12/2 = 6.
Answer:
6
Step-by-step explanation: 4 ÷ (2 ÷3)=6
find the first four terms of the sequence given by the following

Answers
Answer:
42, 38, 34, 30
Step-by-step explanation:
You want the first 4 terms of the sequence described by ...
an = 42 -4(n -1), n ∈ ℕ
Arithmetic sequenceYou can write the first 4 terms of the sequence by evaluating the 'an' expression for n = 1, 2, 3, 4.
Or, you can recognize the expression describes a sequence with a first term of 42 and a common difference of -4. That is, each term is 4 less than the one before.
The terms you want are ...
42, 38, 34, 30
__
Additional comment
The equation for the n-th term of an arithmetic sequence is ...
an = a1 +d(n -1)
where a1 is the first term, and d is the common difference. Comparing this to the given equation, we see a1 = 42, d = -4.
<95141404393>

Marking brainliest
In what ways do you think tree planting is important?
Answers
Answer:
Trees contribute to their environment by providing oxygen, improving air quality, climate amelioration, conserving water, preserving soil, and supporting wildlife. During the process of photosynthesis, trees take in carbon dioxide and produce the oxygen we breathe.
Trees give off oxygen that we need to breathe. Trees reduce the amount of stormwater runoff, which reduces erosion and pollution in our waterways and may reduce the effects of flooding. Many species of wildlife depend on trees for their habitat. Trees provide food, protection, and homes for many birds and mammals.
They give us clean water to drink, air to breathe, shade, and food to humans, animals, and plants. They provide habitats for numerous species of fauna and flora, firewood for cooking and heat, materials for buildings and places of spiritual, cultural, and recreational importance.
PLEASE PLEASE PLEASEEE! THIS IS DUE TOMORROW! ILL THANKS AND WHAT EVER ELSE I CAN TO WHOEVER GETS THIS!

Answers
1.Y=-2/6 -5
2. >
3.<
4. False because the y intercept could be a positive or negative.
That's the best I got.
Which of the binomials below is a factor of this trinomial? x² + 2x - 63 O A.X-3 OB. X+3 O C. X-9 O D. X + 9
Answers
Answer:
D. X + 9
Step-by-step explanation:
x² + 2x - 63
What 2 numbers multiply to -63 and add to 2
9 * -7 = -63
9+-7 = 2
(x+9)(x-7)
help me help me please

Answers
Answer:
a = B
b = E
c = D
d = A
e = C
Step-by-step explanation:
Answer:
you are a very st*pid very f**cking girl d*mb*ss kid
Step-by- step explanation:
if its assumptions are met, the analysis of variance technique is appropriate when ____.
Answers
Answer:
comparing the means of three or more groups
Step-by-step explanation:
(2.569
3
2. Stephanie has 3 bags of soil to put in her garden. Each bag of soil will cover 125 ft.
How many square feet will Stephanie be able to cover if she uses all these bags of soil?
(7.3A)
Answers
i cant understand your question define briefly
Two cars are traveling along a straight road. Car A maintains a constant speed of 77.0 km/h. Car B maintains a constant speed of 114 km/h. At t=0, car B is 45.0 km behind car A. How long does it take before car A is overtaken by car B?
Answers
Answer: 72.97 Minutes
Step-by-step explanation: We have two cars, A and B, traveling along a straight road. Car A is moving at a constant speed of 77.0 km/h, while car B is moving at a constant speed of 114 km/h. At the starting point (t=0), car B is 45.0 km behind car A.
To figure out how long it takes for car B to catch up and overtake car A, we need to consider their relative speeds. The relative speed is the difference between the speed of car B and the speed of car A.
Relative speed = Speed of car B - Speed of car A
Relative speed = 114 km/h - 77.0 km/h
Relative speed = 37.0 km/h
So, car B is moving 37.0 km/h faster than car A. Now, we need to determine the time it takes for car B to cover the initial distance between them, which is 45.0 km.
To calculate time, we use the formula: Time = Distance / Speed. In this case, the distance is 45.0 km, and the speed is the relative speed of 37.0 km/h.
Time = 45.0 km / 37.0 km/h ≈ 1.2162 hours
Now, let's convert the time to minutes by multiplying it by 60 (since there are 60 minutes in an hour).
Time = 1.2162 hours * 60 minutes/hour ≈ 72.97 minutes
Therefore, it takes approximately 1.2162 hours or 72.97 minutes for car B to catch up and overtake car A.
Hope this helps!
4x^2-15x-4
factorise please
Answers
______________________________
1.) Change the equation using factored transformation: \(4x^2-15x-4=0\)- Quadratic polynomial can be factored using the transformation \(ax^2+bx+c=a(x-x_{1})(x-x_{2})\), where \(x_{1}\) and \(x_{2}\) are the solutions of the quadratic equation \(ax^2+bx+c=0\).
- This steps basically means change you current equation using the formula \(ax^2+bx+c=0\).
2.) Turn the factored form into the quadratic equation form:\(x=\frac{-(-15)\frac{+}{}\sqrt{(-15)^2-4\bold{x}4(-4)}}{2\bold{x}4}\)- All equations of the form \(ax^2+bx+c=0\) can be solved using the quadratic formula: \(\sqrt{\frac{-b\frac{+}{}\sqrt{b^2-4ac}}{2a} }\).
- The quadratic equation formula gives two solutions, one when \(\frac{+}{}\) is addition and one when it is subtraction.
3.) Square -15:\(-15^2=225\)
Equation at the end of Step 3:
\(x=\frac{-(-15)\frac{+}{}\sqrt{225-4\bold{x}4(-4)}}{2\bold{x}4}\)4.) Multiply −4 times 4:\(-4\) × \(4=-16\)Equation at the end of Step 4:
\(x=\frac{-(-15)\frac{+}{}\sqrt{225-16(-4)}}{2\bold{x}4}\)5.) Multiply −16 times −4:\(-16\) × \(-4=64\)Equation at the end of Step 5:
\(x=\frac{-(-15)\frac{+}{}\sqrt{225+64}}{2\bold{x}4}\)6.) Add 225 to 64:\(225+64=289\)Equation at the end of Step 6:
\(x=\frac{-(-15)\frac{+}{}\sqrt{289}}{2\bold{x}4}\)7.) Take the square root of 289:\(\sqrt{289}=17\)Equation at the end of Step 7:
\(x=\frac{-(-15)\frac{+}{}17}{2\bold{x}4}\)8.) Change -15 to positive 15:\(-15=15\)Equation at the end of Step 8:
\(x=\frac{15\frac{+}{}17}{2\bold{x}4}\)9.) Multiply 2 by 4:\(2\) × \(4=8\)Equation at the end of Step 9:
\(x=\frac{15\frac{+}{}17}8}\) 10.) Now Solve:Now solve the equation \(x=\frac{15\frac{+}{}17}8}\) when \(\frac{+}{}\) is plus.
Add 15 to 17:
\(15+17=32\)\(x=\frac{32}{8}\)Divide 32 by 8:
\(32\) ÷ \(8=4\)\(x=4\)Now solve the equation \(x=\frac{15\frac{+}{}17}8}\) when \(\frac{+}{}\) is minus.
Subtract 15 by 17:
\(15-17=-2\)\(x=\frac{-2}{8}\)Reduce the fraction to lowest terms by extracting and canceling out 2:
\(-2\) ÷ \(-2=-1\) \(8\) ÷ \(-2=-4\)\(x=-\frac{1}{4}\)11.) Factor the expression:Factor the original expression using \(ax^2+bx+c=a(x-x_{1})(x-x_{2})\). Substitute 4 for \(x_{1}\) and \(-\frac{1}{4}\) for \(x_{2}\):
\(4x^2-15x-4=4(x-4)(x-(-\frac{1}{4}))\)Simplify all the expressions of the form \(p-(-q)\) to \(p+q\):
\(4x^2-15x-4=4(x-4)(x+\frac{1}{4})\)Add \(\frac{1}{4}\) to x by finding a common denominator and adding the numerators. Then reduce the fraction to lowest terms if possible:
\(4x^2-15x-4=4(x-4)\bold{x}(\frac{4x+1}{4})\)Cancel out 4, the greatest common factor in 4 and 4:
\(4x^2-15x-4=(x-4)(4x+1)\)______________________________
the rate of college enrollment immediately after high school completion was 67
Answers
The statement " Rate of college enrollment immediately after completing high school was 67% by 1997" is an example of (a) Descriptive Statistics.
The Descriptive statistics involves the use of measures, such as averages, proportions, and frequencies, to summarize and describe the main features of a set of data.
In this statement, the rate of 67% is a summary statistic that describes the proportion of high school graduates who enrolled in college immediately after completing high school in 1997.
Whereas; the inferential statistics involves making inferences or predictions about a population based on a sample of data.
The statement provides a summary statistic for the rate of college enrollment for a specific year, 1997, but it does not provide any inferences or predictions about the rate of college enrollment for other years or other populations , so it denoted a Descriptive Statistics .
The given question is incomplete , the complete question is
What type of Statistics does the statement "the rate of college enrollment immediately after high school completion was 67" represents ?
(a) Descriptive
(b) Inferential
Learn more about Descriptive Statistics here
https://brainly.com/question/29487303
#SPJ4
What type of number is -16.2i
Answers
Answer:
Complex and imaginary number
Step-by-step explanation:
First, let's write the number\(-16.2i\) in the form of \(a+bi\).
\(0+ (-17)i\)
Since \(-16.2i\) can be written in the form of \(a + bi\), where \(a\) and \(b\) are real numbers, it is a complex number.
Also, since \(a=0\), it is also an imaginary number.
\(-16.2i\) is complex and imaginary.
AC is the diameter of the circle. Angle AWB is 120 degrees. How big is arc BC?

Answers
60 degrees is the measure of arc BC from the figure
Circle geometryThe given diagram is a circle with several arc angles
arcAWB = 120 degrees
The line AC is a diameter
Since the sum of angles on a straight line is 180 degrees, hence:
arc AWB + arcBC = 180
arcBC = 180 - arc ZWX
arcBC = 180 - 120
arcBC = 60 degrees
Hence the measure of the arc BC from the diagram is 60 degrees
Learn more on circle geometry here: https://brainly.com/question/24375372
#SPJ1
Subtract
1/13
31
55
62
110
2
3/5
55
7
10
-
3
22. Simplify the answer.
Answers
When we subtract 3 from 22, the simplified answer is 19. The subtraction operation involves removing or deducting one value from another, resulting in the difference between the two quantities.
To subtract 3 from 22, we can perform the subtraction operation as follows:
22
3
19
We align the numbers vertically and subtract each corresponding place value from right to left. In this case, subtracting 3 from 2 requires borrowing or regrouping. However, since 2 is greater than 3, we can directly subtract 3 from 2 and write the difference, which is 1, in the one's place.
Therefore, the simplified answer is 19.
The subtraction process involves taking away or removing a certain quantity from another. In this case, we subtracted 3 from 22, resulting in a difference of 19. The process of simplifying the answer is simply expressing the result in its most concise and reduced form.
By subtracting 3 from 22, we removed 3 units from the original value of 22, leaving us with 19. This can be visualized as taking away three objects from a group of 22 objects, resulting in a remaining count of 19.
In summary, when we subtract 3 from 22, the simplified answer is 19. The subtraction operation involves removing or deducting one value from another, resulting in the difference between the two quantities.
for such more question on simplified
https://brainly.com/question/11680269
#SPJ8
What is the following product?
(~/14 - 3)(/12 +7)
O 2N/42+7N/2-6-/21
O 14-6+N7
• 26 + /21 -/15-/10
2,/42 - 21
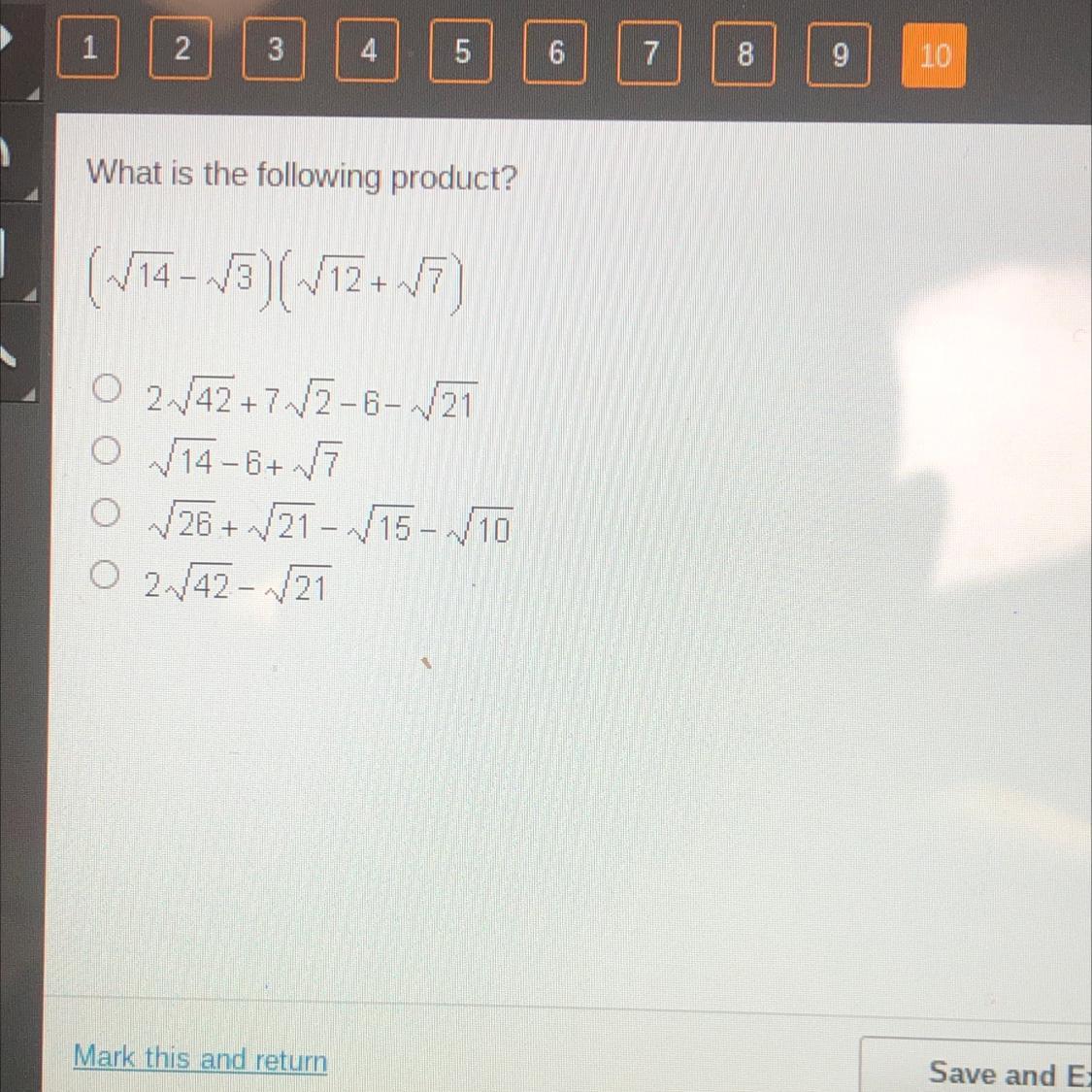
Answers
Option A
Joy's math certificate is 10 inches tall and 13 inches wide. Joy wants to put the certificate in a fancy frame that costs $3.00 per inch. How much will it cost to frame Joy's math certificate?
Answers
In perimeter, The cost to frame Joy's math certificate in a fancy frame is $138.00.
The dimensions of Joy's math certificate are 10 inches tall and 13 inches wide.
Joy wants to frame it in a fancy frame that costs $3.00 per inch.
To determine the total cost of framing the certificate, we need to find its perimeter and then multiply that by the cost per inch.
The perimeter of the certificate is:
Perimeter = 2 × (height + width)
Substituting the given values, we get:
Perimeter = 2 × (10 + 13)Perimeter = 46 inches
Therefore, the total cost of framing Joy's math certificate is:
Total cost = Perimeter × Cost per inch
Total cost = 46 × 3.00Total cost = $138.00
Thus, the cost to frame Joy's math certificate in a fancy frame is $138.00.
Know more about perimeter:
https://brainly.com/question/30252651
#SPJ11
What is the product of d−9 and 2d2+11d−4 ?
Answers
The product of the terms \((d - 9)\) and \((2d^{2} + 11d -4)\) will be \((2d^{3} - 7d^{2} - 103d + 36)\).
We have to find the product of two terms.
First term = (d - 9)
Second term = \((2d^{2} + 11d -4)\)
To find the product of these two terms, we will be using the distributive property. According to the distributive property, when we multiply the sum of two or more addends by a number, it will give the same result as when we multiply each addend individually by the number and then add the products together.
We have to find : \((d - 9) (2d^2 + 11d -4)\)
Using the distributive property,
\(d * 2d^{2} + d * 11 + d * (-4) - 9 * 2d^2 - 9 * 11d - 9 * (-4)\)
After further multiplication, we get
\(2d^{3} + 11d^2 - 4d - 18d^{2} - 99d + 36\)
Now, combine all the like terms.
\(2d^{3} + 11d^{2} - 18d^{2} - 4d - 99d + 36\)
\(2d^{3} - 7d^{2} - 103d + 36\)
Therefore, the product of d-9 and 2d^2 + 11d -4 is \(2d^{3} - 7d^{2} - 103d + 36\)
To learn more about the product and distributive property;
https://brainly.com/question/2807928
#SPJ4