A certain amusement park ride requires riders to be at least 48 inches tall. If the heights of children in a summer camp are normally distributed with mean 52 and standard deviation 2.5, how many of the 140 campers will be allowed on the ride? Round to the nearest integer.
Answers
The 48 inches allowable minimum height of a rider and the 52 and 2.5 mean and standard deviation of the height of the children in the camp of 140 campers, by the Z–Score gives the number of campers allowed as approximately 132 campers.
What is a Z–Score?The required height of riders is at least 48 inches.
The mean height of the children = 52 inches
The standard deviation of the children's height = 2.5 inches
The number of campers at the camp, n = 140
Required: The number of the 140 campers that will be allowed on the ride
Solution:
The Z–Score of the allowable campers is found using the equation;
\(z = \frac{x - \mu}{ \sigma} \)
Which gives;
\(z = \frac{48 - 52}{2.5} = - 1.6\)
From the Z–Score table, the probability (proportion) of a camper's height to be less than 48 inches is P(x < 48) = 0.05480
Therefore;
The probability that the height of a camper is more than 48 inches is given by the equation;
P(x > 48) = 1 - P(x < 48) = 1 - 0.05480
Which gives;
P(x > 48) = 1 - 0.05480 = 0.9452
Which gives;
The number of campers allowed, c, is given by the equation;
c = n × P(x > 48)
c = 140 × 0.9452 = 132.328 ≈ 132
The number of campers allowed is 132 campers.Learn more about the Z–Score of a normal distribution here:
https://brainly.com/question/24213960
#SPJ1
Related Questions
On a coordinate plane, point A is at (negative 1, 3), point B is at (negative 1, negative 3), point C is at (3, negative 3), and point D is at (3, 3). What is the name of the polygon? hexagon octagon quadrilateral triangle
Answers
Answer:
It is a Quadralateral
Step-by-step explanation:
Answer:
quadralatural
Step-by-step explanation:
find the area that the curve encloses and then sketch it. r2 = 9 cos(2θ)
Answers

What is the volume of this rectangular prism?

Answers
Volume = length x width x height.
4 x 1/2 = 2
2 x 3/2 = 3
colume = 3 cubic cm
\(y = \frac{(190)^{3} {68^{2} } \times ( \frac{34}{95}^{ \frac{19}{3} } \)
plz help me solve this question.
Answers
Answer:
\(\dfrac{\sqrt[3]{95^2}}{17\cdot95^4}=\dfrac{\sqrt[3]{9\,025}}{1\,384\,660\,625}\)
Step-by-step explanation:
The applicable rules of exponents are ...
(ab)^c = (a^c)(b^c)
(a^b)/(a^c) = a^(b-c)
__
\(\dfrac{190^3}{68^2}\times\dfrac{34}{95^{\frac{19}{3}}}=\dfrac{(2\cdot 95)^3}{(2\cdot 34)^2}\cdot\dfrac{34}{95^6\cdot 95^{\frac{1}{3}}}=2^{3-2}95^{3-6-\frac{1}{3}}34^{1-2}\\\\=2\cdot 95^{-3\frac{1}{3}}\cdot 34^{-1}=2\cdot 95^{-4+\frac{2}{3}}\cdot 34^{-1}\\\\=\dfrac{2\sqrt[3]{95^2}}{95^4\cdot 34}=\dfrac{\sqrt[3]{95^2}}{17\cdot95^4}\\\\=\dfrac{\sqrt[3]{9\,025}}{1\,384\,660\,625}\)
The base of the mountain is 6,500 feet above sea level and AB measures 230 feet across. Given that the measurements for QAP is 20° and QBP is 35°, how far above sea level is peak P ? Express your answer to the nearest foot.
Height above sea level:

Answers
Answer:
6610
Step-by-step explanation:
We have tan(X) = opposite/ adjacent
tan(QBP) = PQ/BQ
tan(35) = PQ/BQ ---eq(1)
tan(QAP) = PQ/AQ
tan(20) = \(\frac{PQ}{AB +BQ}\)
\(=\frac{1}{\frac{AB+BQ}{PQ} } \\\\=\frac{1}{\frac{AB}{PQ} +\frac{BQ}{PQ} } \\\\= \frac{1}{\frac{230}{PQ} + tan(35)} \;\;\;(from\;eq(1))\\\\= \frac{1}{\frac{230 + PQ tan(35)}{PQ} } \\\\= \frac{PQ}{230+PQ tan(35)}\)
230*tan(20) + PQ*tan(20)*tan(35) = PQ
⇒ 230 tan(20) = PQ - PQ*tan(20)*tan(35)
⇒ 230 tan(20) = PQ[1 - tan(20)*tan(35)]
\(PQ = \frac{230 tan(20)}{1 - tan(20)tan(35)}\)
\(= \frac{230*0.36}{1 - 0.36*0.7}\\\\= \frac{82.8}{1-0.25} \\\\=\frac{82.8}{0.75} \\\\= 110.4\)
PQ = 110.4
≈110
Height above sea level = 6500 + PQ
6500 + 110
= 6610
Write the equation of the line in slope-intercept form.
m=4/7, y-intercept (0,3)
Answers
Answer:
The answer is
\(y = \frac{4}{7} x + 3 \\ \)Step-by-step explanation:
Equation of a line is y = mx + c
where
m is the slope
c is the y intercept
From the question
slope / m = 4/7
y intercept / c = 3
Substitute the values into the above formula
We have the equation as
\(y = \frac{4}{7} x + 3 \\ \)
Hope this helps you
Answer:
\(\boxed {\tt y=\frac{4}{7}x+3}\)
Step-by-step explanation:
Slope-intercept form is:
\(y=mx+b\)
where m is the slope and b is the y-intercept.
We know the slope is 4/7 and the y-intercept is (0,3). In this form, we can say the y-intercept is just 3. Therefore,
\(m=\frac{4}{7}\\b= 3\)
Substitute the values into the form.
\(y=\frac{4}{7} x+3\)
The equation of the line is:
y=4/7x+3
need help pleaseeeeeeeeeeeeee (◕‿◕)╭∩╮

Answers
Answer:
The value 0.031 represents the interest rat, which means the annual compounded interest rate is 3.1%
First option
Step-by-step explanation:
The general equation for amount accrued A with a principal P at an annual compound interest rate of i%(r/100 in decimal) compounded n times a year for t years is given by
\(A = P\left(1 + \dfrac{r}{n}\right)^{nt}\)
Here r = i/100 which is a decimal
Looking at the specific equation
\(A = 2400\left(1 + \dfrac{0.031}{4}\right)^{4t}\)
we can see that P = 2440, the initial investment
0.031 is the annual interest rate in decimal
Expressed as percentage that would be 0.031 x 100 = 3.1% per year
So the correct answer is the first option which states
The value 0.031 represents the interest rat, which means the annual compounded interest rate is 3.1%
consider the system of linear equations
consider the system of linear equations
6x+2y – z=4
X +5y+z=3
2x+y+4z=27
A, solve the system by
I. Gassian elimination method,
II. LU- decomposition method
III. Gauss- Jacobi method,and
IV. Gauss-seidel method,
Answers
I. The solution to the system of equations using Gaussian elimination is x = 1, y = -1, and z = 2.
II. For the LU-decomposition method, we need to have a square coefficient matrix, which is not the case in the given system. Therefore, we cannot directly apply the LU-decomposition method.
III. For this method to converge, the coefficient matrix must be diagonally dominant, which is not the case in the given system. Therefore, the Gauss-Jacobi method cannot be directly applied either.
IV. It requires the coefficient matrix to be diagonally dominant, which is not satisfied in the given system. Hence, the Gauss-Seidel method cannot be directly used.
I. Gaussian Elimination Method:
To solve the system of linear equations using Gaussian elimination, we perform row operations to reduce the system into upper triangular form. The augmented matrix for the given system is:
| 6 2 -1 | 4 |
| 1 5 1 | 3 |
| 2 1 4 |27 |
We can start by eliminating the coefficients below the first element in the first column. To do this, we multiply the first row by a suitable factor and subtract it from the second and third rows to eliminate the x coefficient below the first row. Then, we proceed to eliminate the x coefficient below the second row, and so on.
After performing the necessary row operations, we obtain the following reduced row-echelon form:
| 6 2 -1 | 4 |
| 0 4 2 | -1 |
| 0 0 3 | 6 |
From this form, we can easily back-substitute to find the values of x, y, and z. We have z = 2, y = -1, and x = 1.
II. LU-Decomposition Method:
LU-decomposition is a method that decomposes a square matrix into a product of two matrices, L and U, where L is lower triangular and U is upper triangular.
III. Gauss-Jacobi Method:
The Gauss-Jacobi method is an iterative numerical method to solve systems of linear equations.
IV. Gauss-Seidel Method:
Similar to the Gauss-Jacobi method, the Gauss-Seidel method is an iterative method for solving linear systems.
Therefore, out of the four methods mentioned, only the Gaussian elimination method can be used to solve the given system of linear equations.
For more such questions on solution
https://brainly.com/question/24644930
#SPJ8
please help me it due in an hour

Answers
1. 18x^3-2x^2+4x-1
1.1 How many terms are in 18x^3-2x^2+4x-1
Answers
The polynomial 18x³ - 2x² + 4x - 1 consists of four terms.
The number of terms in a polynomial helps when performing operations like simplification, factoring, or evaluating expressions.
The polynomial 18x³ - 2x² + 4x - 1 consists of four terms.
In order to determine the number of terms in a polynomial, we count the number of distinct algebraic expressions separated by addition or subtraction operations.
In this polynomial, we have:
Term 1: 18x³ (This is the term with the highest degree, which is 3 in this case, and it includes the coefficient 18.)
Term 2: -2x² (This term has a degree of 2 and a coefficient of -2.)
Term 3: 4x (This term has a degree of 1 and a coefficient of 4.)
Term 4: -1 (This is a constant term with a degree of 0.)
We can see that there are four distinct terms separated by addition and subtraction operations:
18x³, -2x², 4x, and -1.
For similar questions on polynomial
https://brainly.com/question/12702996
#SPJ8
I’ll give points + brainalist for correct answer (:

Answers
Answer:
Step-by-step explanation:
i belive its 3
Answer:
the person above me stole my answer
QUESTION 1 Determine the general solution of: 2 sin x. cos x = COS X
Answers
Starting with the given equation: 2 sin x cos x = cos x
By dividing both sides by cos x, we may simplify: 2 sin x = 1
Dividing both sides by 2:
sin x = 1/2
The values of x that fulfil sin x = 1/2 must now be found, and they are:
x = π/6 + 2πn or x = 5π/6 + 2πn, where n is any integer.
Therefore, the general solution is:
x = π/6 + 2πn or
x = 5π/6 + 2πn, where n is any integer.
Learn more about integer here:
https://brainly.com/question/490943
#SPJ1
Average movie prices in the United States are, in general, lower than in other countries. It would cost $78.50 to buy three tickets in Japan plus two tickets in Switzerland. Three tickets in Switzerland plus two tickets in Japan would cost $74.10. How much does an average movie ticket cost in each of these countries?
Answers
The average movie ticket cost in Switzerland and Japan each of these countries is 46.97.
Let's assume that the average cost of a movie ticket in Japan is x, and the average cost of a movie ticket in Switzerland is y.
According to the problem statement, we can write two equations based on the given information:
3x + 2y = 78.5 ...(1)
2x + 3y = 74.1 ...(2)
We can solve these equations simultaneously to find the values of x and y. Here's how:
Multiply equation (1) by 2 and equation (2) by 3, then subtract equation (1) from equation (2):
(2x + 3y) - 2(3x + 2y) = 74.1 - 2(78.5)
Simplifying this equation, we get:
-y = -109.3
Therefore, y = 109.3.
Now substitute y = 109.3 into either equation (1) or (2) and solve for x:
3x + 2(109.3) = 78.5
Simplifying this equation, we get:
3x = -140.9
Therefore, x = -46.97.
However, we cannot have negative ticket prices.
Therefore, the average cost of a movie ticket is 46.97.
To learn more about average cost please click on below link
https://brainly.com/question/31116213
#SPJ1
Circle 1 is centered at (-3,-2) and has a radius of 2 centimeters. Circle 2 is centered at (4,2) and
has a radius of 4 centimeters.
What transformations can be applied to Circle 1 to prove that the circles are similar?
Enter your answers in the boxes.
The circles are similar because you can translate Circle 1 using the transformation
) and then dilate it using a scale factor of
rule (
O(x+7.y+4) scale factor 2
(x+3y+4) scale factor 2
(x+4.y+7) scale factor 2
(x+7.y+4) scale factor-2
Answers
The transformation is a translation (x + 7, y + 4) plus a dilation of scale factor 2.
What transformation can be applied?
We know that Circle 1 is centered at (-3,-2) and has a radius of 2 centimeters, and Circle 2 is centered at (4,2) and has a radius of 4 centimeters.
The radius of circle 2 is twice the radius of circle 1, then we need to have a dilation of scale factor 2.
Now let's apply a translation of (a, b) units such that:
(-3 + a, -2 + b) = (4, 2)
(a, b) = (4 + 3, 2 + 2)
(a, b) = (7, 4)
Then we have the translation (x + 7, y + 4) plus a dilation of scale factor 2.
Learn more about translations at:
https://brainly.com/question/24850937
#SPJ1
2 hr 20 min, 5 hr 15 min
Answers
Answer:
7hrs 35mins
Step-by-step explanation:
addition 2hrs 15 mins +5hrs 20 mins
I Need the Answer to this !!!!!
3(x-2)= 9
Answers
Answer:
x=5
Step-by-step explanation:
Answer : x = 5
3(х-2)= 9
(3)(x) - (3)(2) = 9
3x - 6 = 9
3x = 9 + 6
x = 15 ÷ 3
x = 5 Answer.
Solution set: {5}
Hope that helps...
please help with linear function equations

Answers
Answer:
f(x) = 0.5x
Step-by-step explanation:
For this problem, we simply have to find the constant of proportionality between x and f(x). In other words, what x is multiplied by to get f(x).
Since this proportion is constant (meaning it doesn't change), all we have to do is divide an f(x) value in the table by its corresponding x value.
p = f(x) / x
p = -2 / -4
p = 1/2 = 0.5
We can show the relationship of x to f(x) with the equation f(x) = px, which can be simplified using the constant of proportionality that we just solved for.
f(x) = 0.5x
Five years ago, Max was twice as old as Bert. A year from now, the sum of their ages would be 30. How old are they now? Show your solution.
Answers
Answer:
Bert is 11 years old and Max is 17 years old.
Step-by-step explanation:
System of Equations
To solve the system of equations, we use two variables x and y. Let's make:
x = current age of Max
y = current age of Bert
x - 5 = age of Max five years ago
y - 5 = age of Bert five years ago
x + 1 = age of Max one year from now
y + 1 = age of Bert one year from now
According to the conditions of the problem, five years ago, Max was twice as old as Bert, thus:
x - 5 = 2(y - 5) [1]
It's also known a year from now, the sum of their ages would be 30:
x + 1 + y + 1 = 30 [2]
Operating and simplifying [1]:
x - 5 = 2y - 10
x = 2y - 5 [3]
Operating and simplifying [2]:
x + y + 2 = 30
x + y = 28 [4]
Substituting [3] in [4]:
(2y - 5) + y = 28
Simplifying:
3y - 5 = 28
3y = 33
y = 33/3 = 11
y = 11
From [3]:
x = 2*11 - 5
x = 22 - 5 = 17
x = 17
Max is 17 years old and Bert is 11 years old
Suppose we want to choose 5 colors, without replacement, from 17 distinct colors

Answers
The number of ways to choose the 5 colors from a set of 17 is given as follows:
a) Order matters: 742,560.
b) Order does not matter: 6,188.
How to find the number of ways?When the order matters, the permutation formula is used, given as follows:
\(P_{n,x} = \frac{n!}{(n - x)!}\)
Giving the number of permutations of x elements from a set of n elements.
5 elements are chosen from a set of 17 elements, hence the number of permutations is given as follows:
P = 17!/12! = 742,560.
When the order does not matter, the combination formula is used, given as follows:
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
With the same parameters, the number of ways is given as follows:
C = 17!/(12! x 5!) = 6,188.
More can be learned about the combination formula at https://brainly.com/question/11732255
#SPJ1
7. At the Go Nutty Peanut Company, dry roasted, shelled peanuts are placed in jars by a machine. The
distribution of weights in the glass jars is approximately Normal, with a mean of 17 ounces and a standard
deviation of 0.68 ounces (3 points)
a. What is the probability of randomly selecting 50 jars and finding the average contents to weigh less
than 16.8 ounces?
Answers
The probability of selecting 50 jars is 0%
The z score determines by how many standard deviations the raw score is above or below the mean. It is given by:
\(z=\frac{x-\mu}{\sigma/\sqrt{n} } \\\\where \mu=mean,\sigma=standard\ deviation, x=raw\ score,n=sample\ size\\\\Given\ that\ \mu=17,\sigma=0.68,n=50,x=16.8\\\\z=\frac{16.8-17}{0.65/\sqrt{50} } =-5\)
The P(z < -5) = 0%
Therefore the probability of selecting 50 jars is 0%
Find out more at: https://brainly.com/question/15016913
Find the conjugate and product of the following surds
1) i3 + i5
2) i3 + 9
3) - i2 + 1
4) - 3 + iy
Answers
Answer:
(1) Conjugate = -i8
(2) Conjugate = -i3+9
(3) Conjugate = i2+1
(4) Conjugate = -3-iy
Step-by-step explanation:
From the question,
Conjugate of a surd is formed by changing the sign between a rational number and a surd in an expression.
The conjugate of a surd is obtained by changing the sign of the surd in the expression.
Given
(1) i3+i5 = i8
Conjugate is -i8
(2) i3+9
Conjugate is -i3+9
(3) -i2+1
Conjugate is i2+1
(4) -3+iy
Conjugate is -3-iy
Given rhombus QRST, find the
perimeter if QU = 3 and RU equals 4.
Q
R
T
U
X
S

Answers
The perimeter of the rhombus in this problem is given as follows:
19.8 units.
What is the perimeter of a polygon?The perimeter of a polygon is given by the sum of all the lengths of the outer edges of the figure, that is, we must find the length of all the edges of the polygon, and then add these lengths to obtain the perimeter.
The diagonal length can be obtained as follows:
QU = US = 3.RU = UT = 4.RU + UT = 7.
Applying the Pythagorean Theorem, the side length is obtained as follows:
x² + x² = 7²
2x² = 49
\(x = \sqrt{\frac{49}{2}}\)
x = 4.95.
Then the perimeter is given as follows:
P = 4 x 4.95
P = 19.8 units.
More can be learned about the perimeter of a polygon at https://brainly.com/question/3310006
#SPJ1
Write the number for fourteen million two hundred thousand ?
Answers
Answer:
14,200,000
Step-by-step explanation:
Answer:
There are 1,365 souvenir paperweights that need to be packed in boxes. Each box will hold 14 paperweights. How many boxes will be needed?
boxes will be needed to hold all the souvenir paperweights.
Step-by-step explanation:
Let A be a 7×5 matrix with rank equal to 4 and let b be a vector in R8. The four fundamental sub- spaces associated with A are R(A), N(AT ), R(AT ), and N (A).
Answers
The value of R(A) = 4, N(AT ) = 3, R(AT ) = 4, and N (A) = 3.
Given that
Dimension of matrix = 7×5
Rank of matrix = 4
The range space of A,
Which is a subspace of R, is known as R(A).
It is made up of all conceivable linear combinations of A's columns.
The dimension of R(A) = rank of A,
Which is 4 in this case.
The null space of the transpose of A,
Which is also a subspace of R, is designated as N(AT).
All potential answers to the equation ATx = 0,
Where x is a R column vector, are included in it.
N(AT) has a dimension = nullity of A,
which in this case is 3 in this example.
The range space of the transposition of A, is designated as R(AT).
The rows of A are arranged in all conceivable linear configurations.
The rank of A = 4
Thus it equal to dimension of R(AT).
N(A) is the null space of A.
Axe = 0, where x is a column vector in R, are included in it.
The nullity of AT, which is three, is likewise equivalent to the dimension of N(A).
To learn more about matrix visit:
https://brainly.com/question/29132693
#SPJ1
Maria, Trey, and David sent a total of 65 text messages over their cell phones during the weekend. David sent 2 times as many messages as María, Maria sent 5
fewer messages than Trey. How many messages did they each send?
Answers
Answer:
David= 30
Maria= 15
Trey= 20
Step-by-step explanation:
If David sent 30 messages, then half as as many as that would be 15, the amount that Maria sent. 5 more than what Maria would be what Trey sent, 20.
Which function represents a reflection of f(x) = 3/8 (4)^x across the y-axis?

Answers
A function that represents a reflection of \(f(x) = \frac{3}{8} (4)^x\) across the y-axis include the following: D. \(g(x) = \frac{3}{8} (4)^{-x}\).
What is a reflection over the y-axis?In Mathematics and Geometry, a reflection over or across the y-axis or line x = 0 is represented and modeled by this transformation rule (x, y) → (-x, y).
This ultimately implies that, a reflection over or across the y-axis or line x = 0 would maintain the same y-coordinate while the sign of the x-coordinate changes from positive to negative or negative to positive.
By applying a reflection over the y-axis to the parent exponential function, we would have the following transformed exponential function:
(x, y) → (-x, y).
\(f(x) = \frac{3}{8} (4)^x\) → \(g(x) = \frac{3}{8} (4)^{-x}\)
Read more on reflection here: https://brainly.com/question/3399394
#SPJ1
Help with this question!Please
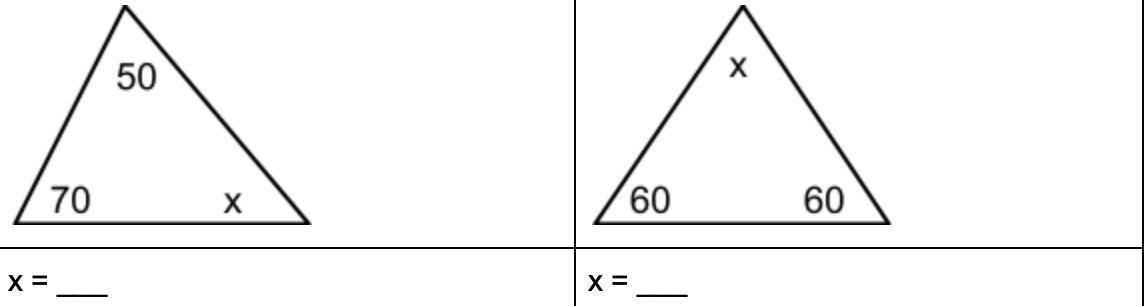
Answers
For both answers X= 60
\({\large\begin{gathered} { \underbrace{\boxed { \rm {\blue {Concept \: \: Using}}}}}\end{gathered}}\)
The angle sum property of a triangle:
Angle sum property of triangle states that the sum of interior angles of a triangle is 180°
\( \underline {\mathcal {{{\color{orange}{\bf \large \rightarrow \: \angle \: 1 \: + \: \angle \: 2 \: + \: \angle \: 3 \: = \: 180 \degree}}}}} \)
\({\large\begin{gathered} { \underbrace{\boxed { \rm {\blue {Solution}}}}}\end{gathered}}\)
In 1st Triangle ∠1 = 50°∠2 = 70°∠3 = x.
\(\bf \large\longrightarrow \: \: 50 \degree \: + \: 70 \degree \: + \: x \: = \: 180 \degree\)
\(\bf \large\longrightarrow \: \:120 \degree \: + \: x \: = \: 180 \degree\)
\(\bf \large\longrightarrow \: \: x \: = \: 180 \degree \: - \: 120 \degree\)
\(\bf \large\longrightarrow \: \: x \: = \: 60\degree\)
_______________________In 2nd Triangle∠1 = x∠2 = 60°∠3 = 60°\(\bf \large\longrightarrow \: \: x \: + \: 60 \degree \: + \: 60 \degree \: = \: 180 \degree\)
\(\bf \large\longrightarrow \: \: x \: + \: 120 \degree \: = \: 180 \degree\)
\(\bf \large\longrightarrow \: \: x \: = \: 180 \degree \: - \: 120 \degree\)
\(\bf \large\longrightarrow \: \: x \: = \: 60\degree\)
M Question 2 Unit 7 Chapter 10 %
https://ezto.mheducation.com/ext/map/index.html?
Account for 63859...Pay your trash bills...
Unit 7 Chapter 10 Quiz
2
Imported from inte...
Wait time
Inspection time
Process time
Seved
New folder
Imported from inte....
17 days
13 days
23 days
22 days
12 days
Navern Corporation manufactures and sells custom home elevators. From the time an order is
placed until the time the elevator is installed in the customer's home averages 87 days. This 87
days is spent as follows:
Help
Move time
Queue time
What is Navern's manufacturing cycle efficiency (MCE) for its elevators?
Seve & Exit
Su
Answers
Navern's manufacturing cycle efficiency (MCE) for its elevators is: 41.4%
How to solve the manufacturing cycle efficiencyThe formula for obtaining the manufacturing cycle efficiency is value-added time divided by the production cycle time * 100. In the data given, the process and inspection times qualify as a value-added time
Process time = 23 days
Inspection time = 13 days
Value added time = 23 + 13 = 36days
The production cycle time = Move time + process time + queue time + inspection time + wait time
= 22 + 12 + 23 + 13 + 17 days
= 87 days
So, the manufacturing efficiency time = 36/87 * 100
= 41.4%
Learn more about manufacturing efficiency here:
https://brainly.com/question/29645032
#SPJ1
If the terminal point determined by t is (-5,-4), then
\sin (t) =
;
\cos (t) =
;
\tan (t) =
.
Answers
Answer:
The trigonometric ratios associated with (-5, -4) are \(\sin t \approx -0.625\), \(\cos t \approx -0.781\) and \(\tan t = 0.8\).
Step-by-step explanation:
Let \(\vec u = (x,y)\). From Trigonometry, we remember the following definitions for the trigonometric ratios, dimensionless:
\(\sin t = \frac{y}{\sqrt{x^{2}+y^{2}}}\) (1)
\(\cos t = \frac{x}{\sqrt{x^{2}+y^{2}}}\) (2)
\(\tan t = \frac{y}{x}\) (3)
If we know that \(x = -5\) and \(y = -4\), then the trigonometric ratios are, respectively:
\(\sin t = \frac{-4}{\sqrt{(-5)^{2}+(-4)^{2}}}\)
\(\sin t \approx -0.625\)
\(\cos t = \frac{-5}{\sqrt{(-5)^{2}+(-4)^{2}}}\)
\(\cos t \approx -0.781\)
\(\tan t = \frac{-4}{-5}\)
\(\tan t = 0.8\)
The trigonometric ratios associated with (-5, -4) are \(\sin t \approx -0.625\), \(\cos t \approx -0.781\) and \(\tan t = 0.8\).
Desiree writes songs for her band. her first song is 3 1/2 minutes long. Her second song is 1 1/2 times as long as her first song. her third song is 2/3 times as long as her second song. How many minutes long are the second and third songs?