A bird flies at an altitude of 520 feet. A diver dives to a depth of 50 feet below sea level. What is the difference in their elevations? Show how you arrived at your answer.
Answers
Answer:
The answer is 570 feet.
Step-by-step explanation:
First, the bird is 520 feet HIGH.
The diver is 50 feet BELOW sea level, which is also -50.
To find the difference, you would SUBTRACT right?
So 520 - -50 OR 520 + 50 (This is because two negatives make a positive, and you are also subtracting negatives, which in turn means adding).
520 + 50 = 570 - HOPE THIS HELPED!
Related Questions
Purchases made at small "corner stores" were studied by the authors of a certain paper. Corner stores were defined as stores that are less than 200 square feet in size, have only one cash register, and primarily sell food. After observing a large number of corner store purchases in Philadelphia, the authors reported that the average number of grams of fat in a corner store purchase was 21.8. Suppose that the variable
x = number of grams of fat in a corner store purchase
has a distribution that is approximately normal with a mean of 21.8 grams and a standard deviation of 7 grams.
a) What is the probability that a randomly selected corner store purchase has more than 29 grams of fat?
b) What is the probability that a randomly selected corner store purchase has between 15 and 25 grams of fat?
c) If two corner store purchases are randomly selected, what it the probability that both of these purchases will have more than 25 grams of fat?
Answers
Answer: x = number of grams of fat in a corner store purchase
has a distribution that is approximately normal with a mean of 21.8 grams
Step-by-step explanation:
2 Mabaso has R140, Thabo has R70 and Ally has R35. What is the ratio of the amount of money Mabaso has, to the amount of money Thabo has and to the amount of money Ally has? Write the ratios in simplest form. The price of a steel table is R750. On Black Friday the table could be bought for R600. Calculate the percentage discount? Show ALL your calculations. Convert 125 g to kilograms. (1 kg = 1 000 grams) A green grocer packs 12 apples in a plastic bag. Calculate the number of bags he w need if he has 285 apples. The scale of a map is 1 500 000. Determine the actual distance in km if measurement on the map is 23,7 cm. Hint: 1 km = 100 000 cm
Answers
The actual distance represented by 23.7 cm on the map is 355.5 km.
To find the ratio of the amount of money Mabaso has to the amount of money Thabo has and the amount of money Ally has, we can divide each amount by the smallest amount (which is R35) to simplify the ratio.
Mabaso has R140, Thabo has R70, and Ally has R35.
The ratio of Mabaso's money to Thabo's money is:
R140 ÷ R35 = 4
The ratio of Mabaso's money to Ally's money is:
R140 ÷ R35 = 4
Therefore, the ratio of the amount of money Mabaso has to the amount of money Thabo has and to the amount of money Ally has is 4:1:1.
To calculate the percentage discount of a steel table, we need to find the difference between the original price and the discounted price, and then divide it by the original price. Finally, we multiply the result by 100 to get the percentage.
Original price: R750
Discounted price: R600
Discount: R750 - R600 = R150
Percentage discount: (R150 ÷ R750) × 100 = 20%
So, the table has a 20% discount on Black Friday.
To convert 125 grams to kilograms, we divide the amount in grams by 1,000 (since there are 1,000 grams in a kilogram).
125 g ÷ 1,000 = 0.125 kg
Therefore, 125 grams is equal to 0.125 kilograms.
If a green grocer packs 12 apples in a plastic bag and has 285 apples, we divide the total number of apples by the number of apples per bag to determine the number of bags needed.
Number of bags needed: 285 apples ÷ 12 apples/bag = 23.75 bags
Since we can't have a fraction of a bag, we round up to the nearest whole number. Therefore, the green grocer would need 24 bags.
If the scale of a map is 1,500,000 and the measurement on the map is 23.7 cm, we can use the scale to determine the actual distance.
1 cm on the map represents 1,500,000 cm in reality.
23.7 cm on the map represents x cm in reality.
x = 23.7 cm × 1,500,000 cm = 35,550,000 cm
To convert cm to km, we divide by 100,000 (since there are 100,000 cm in a kilometer).
35,550,000 cm ÷ 100,000 = 355.5 km
For more such questions on distance
https://brainly.com/question/30395212
#SPJ8
Determine which integer in the solution set will make the equation true.
3s − 12 = −9
S: {−1, 0, 1, 2}
A: −1
B: 0
C: 1
D: 2
Answers
Answer:
c) 1
Step-by-step explanation:
Solving for the value of s,
→ 3s - 12 = -9
→ 3s = -9 + 12
→ s = 3/3
→ [ s = 1 ]
Thus, option (c) is correct.
(9 + r) – (r + 10) please help me simplifying
Answers
The answer is 19
x -10 -3 4 11
y 1 6 30 120
Is the relationship linear, exponential, or neither?
Choose 1 answer:
Choose 1 answer:
A
Linear
B
Exponential
c
Neither
Answers
Answer:
Option C, neither.
Step-by-step explanation:
Here we have the table:
x: -10 -3 4 11
y: 1 6 30 120
This means that if our function is f(x), then:
f(-10) = 1
f(-3) = 6
f(4) = 30
f(11) = 120
We want to know if this represents a linear equation or an exponential equation or neither.
First, let's try with a linear equation.
We know that a linear equation can be written as:
f(x) = a*x + b
Then let's input the known values and let's see if this equation works.
We can use two of the known points to get:
f(-10) = 1 = a*-10 + b
f(4) = 30 = a*4 + b
With these equations, we can find the value of a and b, once we find these values, we can see if the equation also works for the other two points.
1 = a*-10 + b
30 = a*4 + b
First, we need to isolate one of the variables in one of the equations.
I will isolate b in the first one:
b = 1 + a*10
Now we can replace this in the other one to get:
30 = a*4 + 1 + a*10
30 = 1 + a*14
30 - 1 = a*14
29 = a*14
29/14 = a = 2.07
and using the equation b = 1 + a*10 we can find the value of b:
b = 1 + 2.07*10 = 1 + 20.7 = 21.7
Then the equation we get is:
f(x) = 2.07*x + 21.7
Now we need to see if this works for the other two points:
for x = -3, we need to get: f(-3) = 6
f(-3) = 2.07*-3 + 21.7 = 15.49
We did not get the value we expected, then we already know that the relationship is not linear.
Now let's see if the relationship can be exponential.
An exponential function is written as:
f(x) = A*(r)^x
Let's do the same as above, let's use two of the known points to find the values of A and r
f(-3) = 6 = A*(r)^(-3)
f(4) = 30 = A*(r)^4
Now we have the system of equations:
30 = A*(r)^4
6 = A*(r)^(-3)
If we take the quotient of these two equations, we get:
(30/6) = (A*(r)^4)/( A*(r)^(-3))
5 = (r^4)*r^3 = r^(4 + 3) = r^7
(5)^(1/7) = r = 1.258
And the value of A is given by:
30 = A*(1.258)^4
30/( (1.258)^4 ) = 11.98
Then the exponential equation is something like:
f(x) = 11.98*(1.258)^x
Now let's see if this equation also works for the other two points:
for x = -10, we should get f(-10) = 1
Let's see that:
f(-10) = 11.98*(1.258)^(-10) = 1.2
And for x = 11 we should get f(11) = 120
f(11) = 11.98*(1.258)^(11) = 149.6
So we get values closer to the ones we should get, but not the exact ones, so this is not an exponential relation.
Then the correct option is C, neither.
Isaiah brought two dozen donuts to a class party. Half of the donuts had vanilla frosting with sprinkles, 2 had strawberry frosting with cream filling, and the rest had chocolate frosting with sprinkles. what fraction of the donuts had sprinkles?
Answers
Answer: 22
Step-by-step explanation:
Two dozen equals 24, divide it in half leaves 12 vanilla sprinkle doughnuts
the remaining 12 minus the 2 strawberry cream equals 10 chocolate sprinkles
add the 10 chocolate plus 12 vanilla to get 22
What is the discriminant of the polynomial below?
4x2 - 20x+ 25
O A. -360
O B. o
O C. 300
O D. -20
Answers
Answer:
B. 0
Step-by-step explanation:
ax² + bx + 1 = 0
discriminant = b² - 4ac
4x² - 20x + 25
a = 4
b = -20
c = 25
b² - 4ac = (-20)² - 4(4)(25) = 400 - 400 = 0
Answer: B. 0
30 points
All of the following ratios are equivalent except_____.
A. 6/4
B. 8 to 12
C. 2:3
D. 6/9
Answers
Answer:
A. 6/4
Step-by-step explanation:
all of the other answers are equivalent to 0.666667
while 6/4 is equivalent to 1.5
Hope this helped :)
Answer:
A. 6/4
Step-by-step explanation:
B, C, and D are all equal to the ratio 2:3.
On the other hand, A is not equivalent to the other 3.
If we simplify A, it gets us the ratio 3:2, instead of 2:3
So, A is the ratio that is not equivalent to the others.
A residential community was polling households to find out whether they wanted to get their TV signal from a satellite or cable. The results are shown in the Venn diagram.
A circle labeled satellite 55 overlaps a circle labeled cable 75. Overlap is labeled 12. 4-column table with 3 rows. First column has no label with entries satellite, not satellite, total. Second column is cable with entries blank, 51%, blank. Third column is not cable with entries a, b, blank. Fourth column is labeled total with entries blank, blank, 100%.
What are the values of a and b in the relative frequency table for the survey results? Round answers to the nearest percent.
a = 82%, b = 3%
a = 38%, b = 50%
a = 38%, b = 3%
a = 93%, b = 19
Answers
The correct answer is:
a = 43%
b = 88%
To determine the values of a and b in the relative frequency table, we need to analyze the information provided in the Venn diagram and the given table.
From the Venn diagram, we can gather the following information:
The circle labeled "satellite" has a value of 55.
The circle labeled "cable" has a value of 75.
The overlap between the two circles is labeled as 12.
Using this information, we can complete the table:
First column - "Satellite":
Entries: Satellite, Not satellite, Total
Total: 55 (as given in the Venn diagram)
Second column - "Cable":
Entries: Blank, 51%, Blank
To find the value for the "Cable" entry, we need to subtract the overlap (12) from the total number of cable users (75).
Cable: 75 - 12 = 63
Therefore, the entry becomes: Blank, 51%, Blank
Third column - "Not Cable":
Entries: a, b, Blank
To find the value for "a," we subtract the overlap (12) from the total number of satellite users (55).
a: 55 - 12 = 43
To find the value for "b," we subtract the overlap (12) from the total number of households (100).
b: 100 - 12 = 88
Therefore, the entries become: 43, 88, Blank
Fourth column - "Total":
Entries: Blank, Blank, 100%
The total number of households is given as 100% (as stated in the question).
Therefore, the values of a and b in the relative frequency table are:
a = 43% (rounded to the nearest percent)
b = 88% (rounded to the nearest percent)
Hence, the correct answer is:
a = 43%
b = 88%
for such more question on values
https://brainly.com/question/27746495
#SPJ8
You have saved $14,000 for a down payment on a house. Your bank requires a minimum down payment of 17%. What is the maximum price you can offer for a home in order to have enough money for the down payment? (Round your answer to two decimal places.)
Answers
The maximum price you can offer for a home is approximately $82,352.94 for a 17% down payment.
To determine the maximum price you can offer for a home, you need to calculate 17% of the total price, which will be your down payment of $14,000.
Let's assume the maximum price you can offer for the home is P dollars.
According to the given information, the down payment requirement is 17% of the total price. So, we can set up the following equation:
\(0.17P = $14,000\)
To solve for P, divide both sides of the equation by 0.17:
P = $14,000 / 0.17
Calculating this expression, we find:
P ≈ $82,352.94
Therefore, the maximum price you can offer for a home in order to have enough money for the 17% down payment is approximately $82,352.94.
For more questions on down payment
https://brainly.com/question/1698287
#SPJ8
Does anyone know how to do this? Please help!

Answers
So that would make the formula: (3.14)R^2-(3.14)r^2 = A
The only unknown variables that you need to find are the radii of the two circles
The smaller circle:
You are given the diameter, and the diameter is 1/2 the radius,
so r= 1/2(11.25) = 5.625
The larger circle:
You are given the width, which is the total added onto the diameter of the smaller circle so:
(11.25+3.75)/2=7.5
and now that you know R, you can plug into the equation found at the start: (3.14)R^2-(3.14)r^2 = A
(3.14)(7.5^2)-(3.14)(5.625^2)=A
A=176.71-99.35
A=77.36 ft^2
A group of friends bought 6 movie tickets. they used a coupon for $2.00 off the cost of one of the tickets, and their total cost with the coupon was $50.50. write an equation that can be used to determine the regular cost C of each movie ticket
Answers
Answer:
each ticket is $8.75
Step-by-step explanation:
c=8$8.75
The equation that can be used to determine the cost of each movie ticket is C = $48.50 / 6.
What is the equation that can be used to determine the cost of each movie ticket?Total cost of the 6 movie tickets = (6 x cost of each ticket) - value of one coupon
50.50 = 6C - $2
Combine similar terms
$50.50 - $2 = 6C
$48.50 = 6C
Divide both sides of the equawtion by 6
C = $48.50 / 6
To learn more about division, please check: https://brainly.com/question/194007
#SPJ2
A cone-shaped paperweight is 5 inches tall, and the base has a circumference of about 12.56 inches. What is the area of a vertical cross section through the center of the base of the paperweight? Use 3.14 for π .
Answers
The area of the vertical cross section through the center of the base of the paperweight is approximately 12.56 square inches.
To find the area of a vertical cross section through the center of the base of the cone-shaped paperweight, we need to determine the radius of the base first.
The circumference of a circle is given by the formula C = 2πr, where C is the circumference and r is the radius. In this case, we know the circumference is about 12.56 inches, so we can set up the equation:
12.56 = 2πr
To solve for r, we divide both sides of the equation by 2π:
r = 12.56 / (2π)
Now we can calculate the radius:
r ≈ 12.56 / (2 × 3.14)
r ≈ 12.56 / 6.28
r ≈ 2 inches
The radius of the base is approximately 2 inches.
Since the vertical cross section passes through the center of the base, the shape of the cross section is a circle. The formula for the area of a circle is A = \(πr^2\), where A is the area and r is the radius.
Now we can calculate the area of the cross section:
A = \(πr^2\)
A ≈ 3.14 × \((2^2)\)
A ≈ 3.14 × 4
A ≈ 12.56 square inches
Therefore, the area of the vertical cross section through the center of the base of the paperweight is approximately 12.56 square inches.
For such more questions on Cone Cross Section Area
https://brainly.com/question/29140252
#SPJ11
Simplify: (39x^5z^4)^0 • 18x^2y
Answers
The simplification of (39x⁵z⁴)⁰ • 18x²y is 18x²y.
What is Simplification?Making anything simpler is known as simplification. In mathematics, simplifying an equation, fraction, or problem means taking it and making it simpler.
To simplify an equation:
By eliminating all common components from the numerator and the denominator and putting the fraction in its simplest/lowest form, we can simplify fractions. Mathematical expressions can be made simpler by grouping and combining related terms.Rewrite the given equation using the commutative property of multiplication.
18(39x⁵z⁴)⁰x²y
Use the power rule (xy)ⁿ=xⁿyⁿ for distributing the exponent.
18(39⁰(x⁵)⁰(z⁴)⁰)x²y
Anything raised to 0 is 1.
18(1(x⁵)⁰(z⁴)⁰x²y
Multiply (x⁵)⁰(x⁵)⁰ by 11.
18((x⁵)⁰(z⁴)⁰)x²y
Multiply the exponents in (x⁵)⁰.
18(x⁰(z⁴)⁰)x²y
Multiply x⁰ by x² by adding the exponents.
18(x²(z⁴)⁰)y
Simplify 18(x²(z⁴)⁰)y
18x²y
Therefore, simplification of given equation is 18x²y.
To learn more about simplification visit:
https://brainly.com/question/23509407
#SPJ9
Please help I am so lost thank you all

Answers
h = hours till they're 58 miles apart
Check the picture below.
so they're travelling in opposite directions, however the combined distances is 58 miles at say "h" hours, by the time that happend Hopi has been walking "h" hours and Brittany has also being walking "h" hours too.
Since the combined distance is 58 miles than if Hopi has covered "m" miles then Brittany covered the slack of "58 - m".
\({\Large \begin{array}{llll} \underset{distance}{d}=\underset{rate}{r} \stackrel{time}{t} \end{array}} \\\\[-0.35em] ~\dotfill\\\\ \begin{array}{lcccl} &\stackrel{miles}{distance}&\stackrel{mph}{rate}&\stackrel{hours}{time}\\ \cline{2-4}&\\ Hopi&m&15&h\\ Brittany&58-m&14&h \end{array}\hspace{5em} \begin{cases} m=(15)(h)\\\\ 58-m=(14)(h) \end{cases} \\\\[-0.35em] ~\dotfill\)
\(\stackrel{\textit{substituting on the 2nd equation}}{58-(\stackrel{m}{15h})=14h}\implies 58=29h\implies \cfrac{58}{29}=h\implies \boxed{2=h}\)

Mustard hot sauce mustard hot sauce
Answers
Answer:
mustard hot sauce
Step-by-step explanation:
mustard hot sauce
Answer:
aww mustard
Step-by-step explanation:
Aww mustard! Come on man, now don’t put no mustard on that you need to put a little season on that thing! WHAT! Man come on get that pepper off there! Come on somebody come get this man! Come on now, come on get that pepper of there, that’s just too much doggone pepper. I dont wanna see this no more
Solve each system of linear equations below, then check your work.
A. 3x−y=−11 −x+y=5
B -2y+3= 4x + 2 6x + 4y=1
C. 32y- x= -25 5x= 100 + x - 8Y
D. 2y + 3x = 6 4x + 5y +20 = 0
Answers
A. The solution of linear equation is (x, y) = (-3, 8).
B. The solution is (x, y) = (3/4, -1).
C. The solution is (x, y) = (-31/8, 3/8).
D. The solution is (x, y) = (55/7, -117/14).
A. 3x - y = -11 --- (1)
-x + y = 5 --- (2)
From equation (2), we can write y = x + 5, and substitute it in equation (1):
3x - (x + 5) = -11
2x = -6
x = -3
Substituting x in equation (2):
-y = -8
y = 8
Therefore, the solution of the system is (x, y) = (-3, 8).
To check the solution, we substitute the values of x and y in the original equations:
3(-3) - 8 = -11 (True)
-(-3) + 8 = 5 (True)
So, the solution is correct.
B. -2y + 3 = 4x + 2 --- (1)
6x + 4y = 1 --- (2)
From equation (1), we can write 4x + 2 = -2y + 3, and substitute it in equation (2):
6x + 4y = 1
6x - 4y = 8 (rearranging)
12x = 9
x = 3/4
Substituting x in equation (1):
-2y + 3 = 4(3/4) + 2
-2y + 3 = 5
-2y = 2
y = -1
Therefore, the solution of the system is (x, y) = (3/4, -1).
To check the solution, we substitute the values of x and y in the original equations:
-2(-1) + 3 = 4(3/4) + 2 (True)
6(3/4) + 4(-1) = 1 (True)
So, the solution is correct.
C. 32y - x = -25 --- (1)
5x = 100 + x - 8y --- (2)
From equation (2), we can write 4x = 100 - 8y, and substitute it in equation (1):
32y - x = -25
32y - (100 - 8y) = -25
40y = 75
y = 3/8
Substituting y in equation (1):
32(3/8) - x = -25
x = -31/8.
Therefore, the solution of the system is (x, y) = (-31/8, 3/8).
To check the solution, we substitute the values of x and y in the original equations:
32(3/8) - (-31/8) = -25 (True)
5(-31/8) = 100 + (-31/8) - 8(3/8) (True)
So, the solution is correct.
D. To solve the system of equations:
2y + 3x = 6 --- (1)
4x + 5y + 20 = 0 --- (2)
We can rearrange equation (2) to isolate one of the variables:
4x + 5y = -20 (subtracting 20 from both sides)
5y = -4x - 20 (subtracting 4x from both sides)
y = (-4/5)x - 4 (dividing both sides by 5)
Substituting this value of y in equation (1):
2((-4/5)x - 4) + 3x = 6
(-8/5)x - 8 + 3x = 6
(-8/5)x + 3x = 14
(-8/5 + 3)x = 14
(-8/5 + 15/5)x = 14
(7/5)x = 14
x = 10
Substituting this value of x in the equation for y:
y = (-4/5)(10) - 4
y = -12.
Therefore, the solution of the system is (x, y) = (10, -12).
To check the solution, we substitute the values of x and y in the original equations:
2(-12) + 3(10) = 6 (True)
4(10) + 5(-12) + 20 = 0 (True)
So, the solution is correct.
For similar question on linear equations.
https://brainly.com/question/2030026
#SPJ11
A population of rare birds in town is currently listed at 2,000. It is declining at a rate of 2% per year. How many birds will be left after 20 years? Round your answer to the nearest whole number.
A. 1,335 birds
B. 1,980 birds
C. 2,972 birds
D. 23 birds
Answers
Option(A) is the correct answer is A. 1,335 birds.
To calculate the number of birds that will be left after 20 years, we need to consider the annual decline rate of 2%.
We can use the formula for exponential decay:
N = N₀ * (1 - r/100)^t
Where:
N is the final number of birds after t years
N₀ is the initial number of birds (2,000 in this case)
r is the annual decline rate (2% or 0.02)
t is the number of years (20 in this case)
Plugging in the values, we get:
N = 2,000 * (1 - 0.02)^20
N = 2,000 * (0.98)^20
N ≈ 2,000 * 0.672749
N ≈ 1,345.498
Rounded to the nearest whole number, the number of birds that will be left after 20 years is 1,345.
for similar questions on population.
https://brainly.com/question/30396931
#SPJ8
simplify 4 x 18/6 x 5/5
Answers
Answer:
12
Step-by-step explanation:
4.18/6 * 5 over 5
72/6 *5 over 5
72/6 * 5 divided by 5
12.5 divided by 5
12 times 5 over 5
60/5
60 divided by 5
What is the area of this figure?
Enter your answer in the box.
___in^2

Answers
Answer:
400
Step-by-step explanation:
8*20/2+16*20=400.
describe the possible values of a
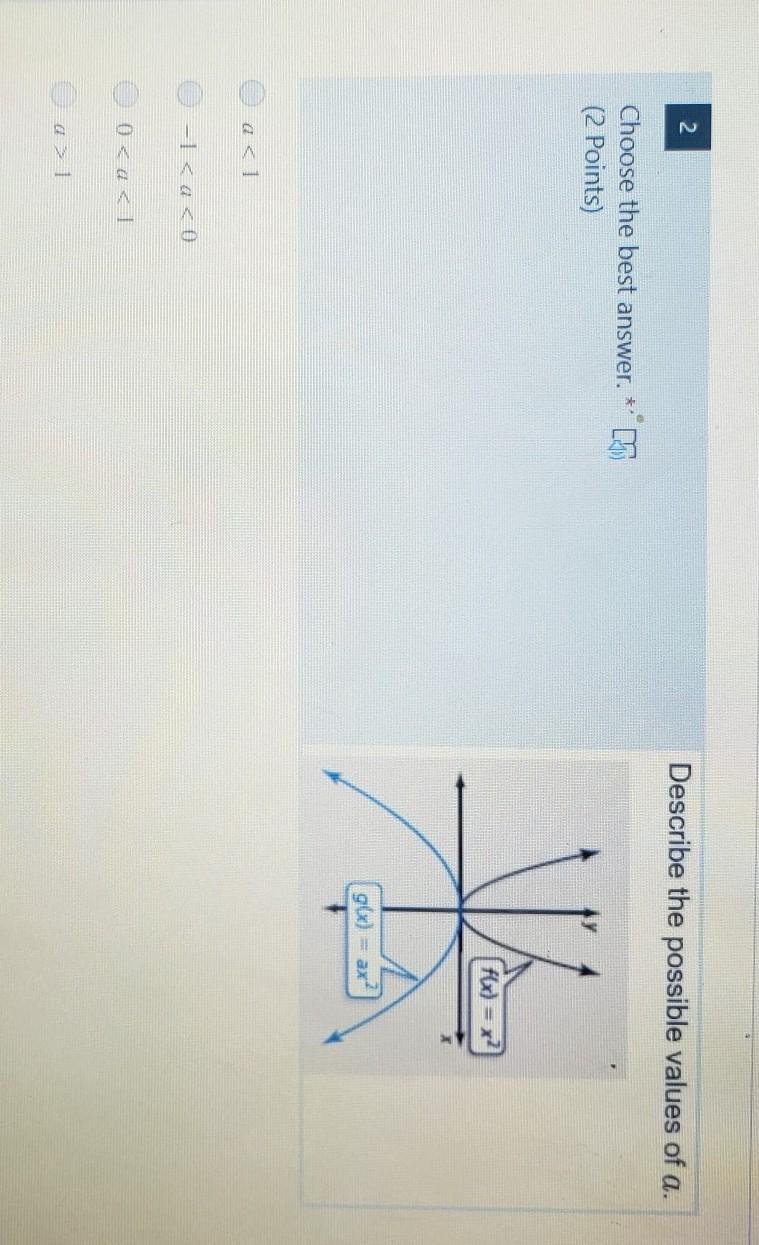
Answers
Answer:
its the second one can u make me brain list
Step-by-step explanation:
The customer service department of a company found that the relationship between the number of minutes a customer spends on hold when telephoning and the customer's level of satisfaction on a 10-point scale can be approximated by the equation y=10−0.1x
, where x
is the number of minutes on hold and y
is the level of satisfaction. What does 0.1 represent in the equation?
Answers
In the equation y = 10 - 0.1x, the coefficient 0.1 represents the slope of the line.
Define slopeit represents the rate of change of y with respect to x, which is the amount by which y changes for every unit increase in x.
In this case, the slope is negative (-0.1), which means that as the number of minutes on hold (x) increases by 1 unit, the level of satisfaction (y) decreases by 0.1 units.
In other words, the longer a customer spends on hold, the lower their level of satisfaction is likely to be. The slope is a key parameter in the equation and provides valuable information about the relationship between the two variables.
To Know more about variables, visit:
https://brainly.com/question/17344045
#SPJ1
Add -2 + (-7) = what is the answer
Answers
Answer: -9
Step-by-step explanation: 2 + 7 = 9 and just put an negative in front of 9
-9 -_-Answer:
-2+(-7) is the question
-2-7 + and - together makes -
-9 you add when the numbers have a sign of - and -
The scale of a map is 1:100. what area does 1 cm² on the map represent? what area does 6 cm² represent?
Answers
1cm^2 : 10000cm^2
6cm^2 : 60000cm^2
A quarterback can throw football 0.04 miles how many throws would it take for him to throw the ball into a pond that is 35.6 miles away
Answers
Answer: 890 throws
Step-by-step explanation: divide 35.6 by 0.04
to get your answer.
Bc thats just what it is
If you added another layer of unit cubes on top of prism a what would the volume of the new solid be in cubic units
Answers
The volume of the new solid with an additional layer of unit cubes on top of the prism is 16 cubic units. This can be calculated by multiplying the area of the base (4 square units) by the height (2 units) and adding the volume of the extra layer (8 cubic units).
If another layer of unit cubes is added on top of a prism, the volume of the new solid will be 8 cubic units. This can be calculated by multiplying the area of the base of the prism by its height. A prism is a 3D shape with two parallel, congruent bases. The base of this prism is a square with a side length of 2 units. The area of this square can be calculated by squaring the side length, so the area of the base is 2 x 2 = 4 square units. The height of the prism is also 2 units. When multiplied together, the volume of the prism is 4 x 2 = 8 cubic units. When another layer of unit cubes is added, this extra layer adds another 8 cubic units to the volume, making the overall volume of the new solid 8 + 8 = 16 cubic units.
Learn more about volume here:
https://brainly.com/question/28338582
#SPJ1
Need help ASAP ‼️
The subject is trigonometric ratios.

Answers
Answer:
4/9 that's the answer tan s = opp/adj
Jose has scored 166 points on his math tests so far this semester. To get an A for the semester, he must
score at least 248 points.
Part 1 out of 2
Enter an inequality to find the minimum number of points he must score on the remaining tests in order to
get an A. Let n represent the number of points Jose needs to score on the remaining tests.
The inequality is
+ n (select)
Next

Answers
Answer: 166 + n >= 248. <-- We use >= symbol since at least means greater than or equal to.
166 + n >= 248
n >= 82
Step-by-step explanation:
Answer:
Step-by-step explanation:
\(166+n\ge 248\)
The graph below shows the solutions to which inequality?
A. x^2-3x+3 ≥0
B. x² + 3x-3 <0
C. x²-3x+3<0
D. x² + 3x-3>0
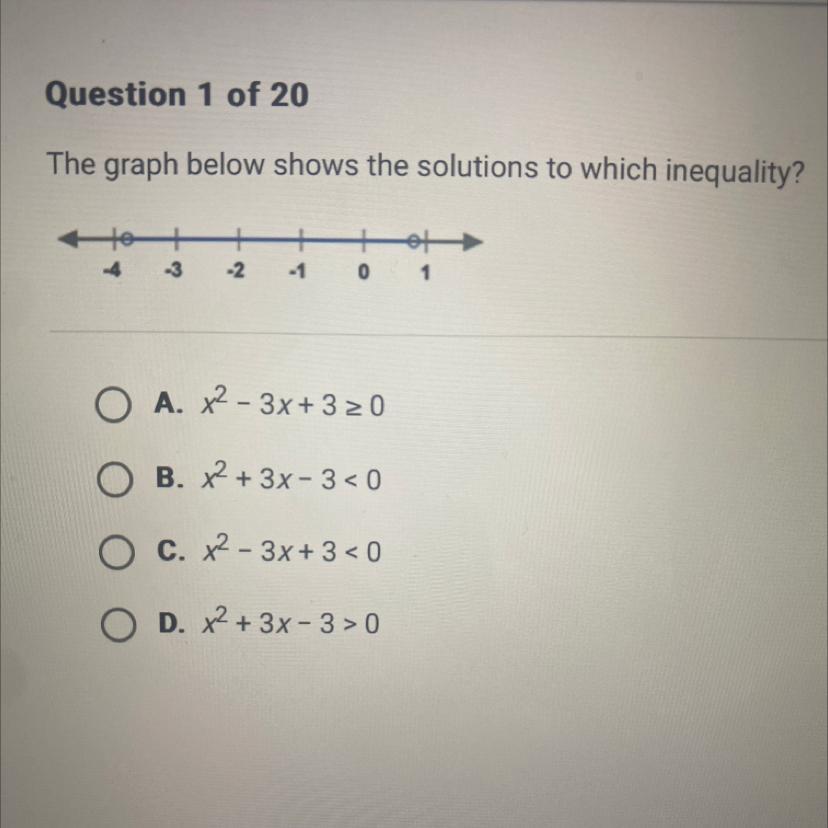
Answers
The inequality expression that corresponds to the solution of the inequality graph is x² + 3x - 3 < 0.
option B.
What is the solution of the inequality?The inequality expression that corresponds to the solution of the inequality graph is determined by simplifying the equations as follows;
The solution of the graph,
x > -4 and x < 1
The first equation with "≥" is ruled out because the graph doesn't have a thick dot.
Let's simplify the second expression;
x² + 3x - 3 < 0
solve using quadratic formula;
x > -3.79 or x < 0.79
The third expression is ruled out since its solution will be complex.
For the last expression;
x² + 3x - 3 > 0
x < -3.79 or x > 0.79
Thus, the correct inequality expression is x² + 3x - 3 < 0.
Learn more about inequality expression here: https://brainly.com/question/25275758
#SPJ1
Solve for the missing side length. Round to the nearest tenth.
5.8
5.2
5.4
5.6

Answers
Answer:
C) 5.4-------------------------
Given two legs of a right triangle and we need to find the hypotenuse.
Use Pythagorean theorem:
\(PQ = \sqrt{QR^2+PR^2}\)\(PQ = \sqrt{2^2+5^2} =\sqrt{29} =5.385 = 5.4\ (rounded)\)The matching choice is C.