A 90% confidence interval is constructed based on a sample of data, and it is 74% +3%. A 99% confidence interval based on this same sample of data would have: A. A larger margin of error and probably a different center. B. A smaller margin of error and probably a different center. C. The same center and a larger margin of error. D. The same center and a smaller margin of error. E. The same center, but the margin of error changes randomly.
Answers
As a result, for the same data set, a 99% confidence interval would have a greater margin of error than a 90% confidence interval.
Answer: If a 90% confidence interval is constructed based on a sample of data, and it is 74% + 3%, a 99% confidence interval based on this same sample of data would have a larger margin of error and probably a different center.
What is a confidence interval? A confidence interval is a statistical technique used to establish the range within which an unknown parameter, such as a population mean or proportion, is likely to be located. The interval between the upper and lower limits is called the confidence interval. It is referred to as a confidence level or a margin of error.
The confidence level is used to describe the likelihood or probability that the true value of the population parameter falls within the given interval. The interval's width is determined by the level of confidence chosen and the sample size's variability. The confidence interval can be calculated using the standard error of the mean (SEM) formula
.A 90% confidence interval indicates that there is a 90% chance that the interval includes the population parameter, while a 99% confidence interval indicates that there is a 99% chance that the interval includes the population parameter.
When the level of confidence rises, the margin of error widens. The center, which is the sample mean or proportion, will remain constant unless there is a change in the data set. Therefore, alternative A is the correct answer.
To know more about margin visit:
https://brainly.com/question/15357689
#SPJ11
Related Questions
Help me please no links

Answers
Answer: C
3sqrt2
Step-by-step explanation:
Bro this is so hard
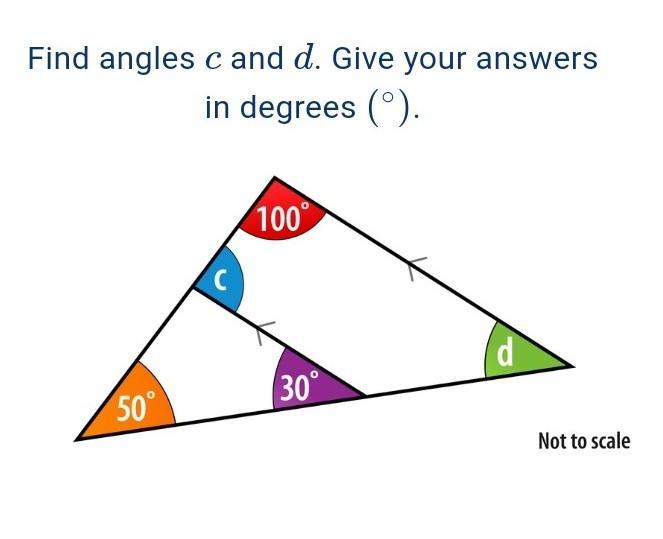
Answers
Answer:
c = 50 degrees and d = 30 degrees
Answer:
C = 80 degrees
D = 30 degrees
Step-by-step explanation:
To find the angle of C you have to add the other angles of that triangle. The total angle of a triangle is 180 degrees.
50 + 30 = 80
Subtracted 80 from 180 to get the other missing angle next to angle c. That is 100. A straight line is 180 degrees so you get 80 degrees for angle C.
To find the angle of D you add angle C, which is 80, to the 100 degree angle and get 180. The total degrees for a four-sided shape is 360 degrees. Then you try to figure out the other missing angle next to the 30-degree angle. A straight line is 180 degrees so subtract 30 from 180 to get the value of the missing angle.
180 - 30 = 150
Add the 180 degrees from earlier to 150 and you get 330. Subtract 330 from 360 and you get 30 degrees. Therefore the angle for d is 30 degrees.
Express 9.25. as a fraction in its simplest form
Answers
Answer:
9 1/4
Step-by-step explanation:
9.25-9=0.25
0.25 =1/4
9 1/4
The vertex of the graph of f(x)=|X-3|+6 is located at

Answers
The vertex of the graph of f(x)= |x-3|+6 is located at (3, 6)
How to determine the vertex?The equation of the function is given as:
f(x) = |x - 3| + 6
The above function is an absolute value function.
An absolute value function is represented as:
f(x) = a|x - h| + k
Where:
Vertex = (h, k)
By comparison, we have:
Vertex = (3, 6)
Hence, the vertex of the graph of f(x)= |x-3|+6 is located at (3, 6)
Read more about vertex at:
https://brainly.com/question/16799565
#SPJ1
Witch shows 9 groups of 3 ?
Answers
Answer:
3
Step-by-step explanation:
If 3 quantities are equally divided in 9 groups, then each group will contain 1/3 of such quantities, which is one-third of one of such considered quantities.
How can we interpret the division?When 'a' is divided by 'b', then the result we get from the division is the part of 'a' that each one of 'b' items will get.
Thus, if 10 mangoes are there, and 2 people, then 10 ÷ 2 is the number of mangoes each person would get, which is 5.
Division, thus, can be interpreted as equally dividing the number that is being divided in total x parts, where x is the number of parts the given number is divided.
Thus, \(a \div b\)equal parts.
Also, we can write: \(a \div b = a \times \dfrac{1}{b}\)
(it is since a = a times 1 so \(a/b = 1 \times (a/b) = (1/b) \times a\) )
Suppose that the question is asking us to find the quantity each group will possess of those 3 quantities which is divided into 9 groups equally (assumingly).
3 quantities to be divided into 9 groups of equal quanties, or say 9 equal parts.
Thus, the quanity each part would get is:
\(3 \div 9 = \dfrac{3}{9} = \dfrac{1 \times 3}{3 \times 3} = \dfrac{1}{3} \: \rm quantities\)
1/3 shows one-third of the considered quantity which was available in 3 units and was divided in 9 groups, each having equal amount of that quantity.
Thus, if 3 quantities are equally divided in 9 groups, then each group will contain 1/3 of such quantities, which is one-third of one of such considered quantities.
Learn more about division here:
https://brainly.com/question/26411682
#SPJ2
An equilateral triangle has a perimeter of 12x+ 18 units. Which expression can be used to show the length of one side of
the triangle?
6(2x+3): Each side length is 2x+ 3 units.
3(4x+6). Each side length is 4x+6 units.
2(6x+9). Each side length is 6x+9 units.
x(12+ 18). Each side length is 12+ 18 units.
Answers
Answer:
b
Step-by-step explanation:
four less than twice a number
Answers
Answer:
as per ur ques if we take x as number then we get algebraic expression as
2x - 4
brainliest?
2x-4
lynn has one red shirt one blue shirt and one yellow shirt to choose from. She also has one blue and one yellow necklace to choose from for work today are these values dependent or independent
Answers
I would say the answer is depending. the reason I choose this answer because she chose a random shirt, which she probably chose a necklace that would look best with the shirt she had randomly had choosen.
ITS BEEN OVER 48 HRS SINCE I FIRST POSTED THIS QUESTION PLEASE HELP ME IF YOU CAN :((((((((((!!!!!!!!!!!!!!!!!!!!!!!!!
Find the volume of the pyramid. SHOW YOUR WORK so I can see if the answer makes sense.

Answers
Step-by-step explanation:
we know,
volume of pyramid = 1/3 × base area × height
so,
→ 1/3 × 120 × 9
→ 40 × 9 = 360 ft
so the volume of the pyramid is 360 ft².
base area = length × slant height
so, 12 × 10 = 120
hope this answer helps you dear....take care and may u have a great day ahead dear !
Fill in the missing statements and reasons in this proof. Number your reasons 1 through 5 as they would be shown in the chart below.
Given: m∠LOM = m∠JKI;
m∠MON = m∠IKH
Prove: m∠LON = m∠HKJ
would rlly appreciate ur help

Answers
From the given condition m ∠LOM = m ∠JKI, m ∠MON = m ∠IKH it is proved that m ∠LON = m ∠HKJ as they are congruent angles.
What are congruent angles?Congruent angles are defined as angles with equal measure. According to the question,
m ∠LOM = m ∠JKI (given congruent angles) _____(1)
m ∠MON = m ∠IKH (given congruent angles) _______(2)
Add both the side angle m ∠MON in (1) we get m ∠LOM + m ∠MON = m ∠JKI + m ∠MON
Replace angle m ∠MON = m ∠IKH from (2) on right-hand side we get,
m ∠LOM + m ∠MON = m ∠JKI + m ∠IKH ____(3)
m ∠LOM + m ∠MON = m ∠LON ( M is the interior point of ∠LON) ___(4)
m ∠JKI + m ∠IKH = m ∠HKJ ( I is the interior point of ∠HKJ) ___(5)
Form (3), (4), and (5) we get, m ∠LON = m ∠HKJ (Congruent angles)
Hence, from the given condition it is proved that m ∠LON = m ∠HKJ, are congruent angles.
Learn more about congruent angles on:
brainly.com/question/24887947
#SPJ1
help asap no wrong answers----------------------

Answers
Answer:
\(y=-2(sin(2x))-7\)
Step-by-step explanation:
1. Approach
Given information:
The graph intersects the midline at (0, -7)The graph has a minimum point at (\(\frac{\pi}{4}\), 9).What conclusions can be made about this function:
The graph is a sine function, as its y-intercept intersects the midlineThis graph has a negative coefficient, this is because after intersecting the midlines at the y-intercept, the function has a minimum.This graph does not appear to have undergone any horizontal shift, as it intercepts the midlines with its y-interceptTherefore, one has the following information figured out:
\(y=-n(sin(ax))+b\)
Now one has to find the following information:
amplitudemidlineperiod2. Midline
The midlines can simply be defined as a line that goes through a sinusoidal function, cutting the function in half. This is represented by the constant (b). One is given that point (0, -7) is where the graph intersects the midline. The (y-coordinate) of this point is the midline. Therefore, the midline is the following:
y = -7
2. Amplitude
The amplitude is represented by the coefficient (n). It can simply be defined by the distance from the midline to point of maximum (the highest part of a sinusoidal function) or point of minimum (lowest point on the function). Since the function reaches a point of minimum after intercepting the (y-axis) at its midlines, the amplitude is a negative coefficient. One can find the absolute value of the amplitude by finding the difference of the (y-coordinate) of the point of minimum (or maximum) and the absolute value of the midline.
point of minimum: \((\frac{\pi}{4},9)\)
midline: \(y=-7\)
Amplitude: 9 - |-7| = 9 - 7 = 2
3. Period
The period of a sinusoidal function is the amount of time it takes to reach the same point on the wave. In essence, if one were to select any point on the sinusoidal function, and draw a line going to the right, how long would it take for that line to reach a point on the function that is identical to the point at which it started. This can be found by taking the difference of the (x- coordinate) of the intersection point of the midline, and the (x-coordinate) of the point of minimum, and multiplying it by (4).
point of minimum: \((\frac{\pi}{4},9)\)
midline intersection: \((0, -7)\)
Period: \(4(\frac{\pi}{4}-0)=4(\frac{\pi}{4})=\pi\)
However, in order to input this into the function in place of the variable (a), one has to divide this number by (\(2\pi\)).
\(a=\frac{2\pi}{\pi}=2\)
4. Assemble the function
One now has the following solutions to the variables:
\(n =-16\\a=2\\b=-7\\\)
Substitute these values into the function:
\(y=-2(sin(2x))-7\)
when a person's test performance can be compared with that of a representative and pretested sample of people, the test is said to be group of answer choices reliable. standardized. valid. normally distributed.
Answers
When a person's test performance can be compared with that of a representative and pretested sample of people, the test is said to be standardized.
Standardization refers to the process of establishing norms or standards for a test by administering it to a representative and pretested sample of individuals. This allows for a comparison of an individual's test performance to that of the larger group. When a test is standardized, it means that it has undergone rigorous development and validation procedures to ensure that it is fair, consistent, and reliable.
Standardized tests provide a benchmark for evaluating an individual's performance by comparing their scores to those of the norm group. The norm group consists of individuals who have already taken the test and represents the population for which the test is intended. By comparing an individual's scores to the norm group, it is possible to determine how their performance ranks relative to others.
Therefore, when a person's test performance can be compared with that of a representative and pretested sample of people, it indicates that the test is standardized. Standardization is an essential characteristic of reliable and valid tests, as it ensures consistency and allows for meaningful comparisons among test-takers.
Learn more about consistent here:
https://brainly.com/question/29243659
#SPJ11
20 POINTS HELP, WILL GIVE BRAINLIEST IF CORRECT! (Only if two people answer I will give brainliest)

Answers
Answer:
Bottom(equation 3)=No solution
Middle(equation 2)= Infinite solutions
Top(equation 1)=1 solution
Step-by-step explanation:
Brainly pls I hope this helps
2) infinite solutions
3) no solutions
11. Find x, y, and z.
5
y
6
3

Answers
Answer:
x = z = 3√5y = 4Step-by-step explanation:
You want the missing segment lengths in the kite shown, where half-diagonals are 3 and 6, and one side length is 5.
KiteThe diagonals of a kite cross at right angles, so each of the triangles shown is a right triangle. The figure has left-right symmetry about the vertical axis, so x=z.
Length yWe recognize the top triangles as being 3-4-5 right triangles, so the missing side length is y = 4.
Lengths x and zThese lengths are the hypotenuse of a right triangle with legs 3 and 6. The Pythagorean theorem tells us they are ...
x² = 3² +6²
x² = 9 +36 = 45
x = √(45) = √(9·5) = 3√5
The lengths x and z are ...
x = z = 3√5
__
Additional comment
In case you have never heard of a 3-4-5 right triangle, you can find y from the Pythagorean relation:
5² = 3² +y²
y² = 25 -9 = 16
y = √16 = 4
The {3, 4, 5} Pythagorean triple is one of several in common use in algebra, trig, and geometry problems. Others include {5, 12, 13}, {7, 24, 25}, {8, 15, 17}.
A survey of 1720 parents of 13- to 17-year-olds found that 678 of the 1720 parents have checked their teen's social media profile. Identify the population. Choose the correct answer below. A. The collection of responses of all parents B. The collection of responses of the 678 parents of 13- to 17-year-olds who said they have checked their teen's social media profile C. The collection of responses of the 1720 parents of 13- to 17-year-olds surveyed D. The collection of responses of parents of 13- to 17-year-olds Identify the sample
Answers
The population is the collection of parents of 13- to 17-year-olds. The sample is the 1720 parents surveyed.
The population in this survey is option D: the collection of responses of parents of 13- to 17-year-olds. The sample in this case is option C: the 1720 parents of 13- to 17-year-olds who were surveyed.
In this scenario, the population refers to the entire group of interest, which is parents of 13- to 17-year-olds. The survey aims to gather information about this entire group, so the population is defined as the collection of responses from all parents of 13- to 17-year-olds.
On the other hand, the sample is a subset of the population that is selected and surveyed. In this case, the sample consists of the 1720 parents of 13- to 17-year-olds who participated in the survey. The sample is used to gather data and draw conclusions about the larger population.
Learn more about population here:
https://brainly.com/question/31598322
#SPJ11
Help asap brb.asap asap will give max points

Answers
Answer:
\(3^{3}\)
Step-by-step explanation:
Note: When you divide exponents with the same constant, the exponent will be subtracted, and vice-versa, when you multiply exponents with the same constant, the exponents will be added.
\(\frac{3^{-9} }{3^{-12} } \\= 3^{-9-(-12)} \\=3^{-9+12} \\=3^{3}\)
when dividing exponents, you subtract the exponents from each other in this case it would be 9- (-12) which would equal 3
The derivative of f(x) = x3 – 12x + 5 is 3x2 – 12 . Find the coordinates of the turning points of f(x)
Answers
Answer:
(-2, 21) and (2, -11) let me know if anything didn't make sense
Step-by-step explanation:
Try and put the symbols in, so for x to the third power write x^3 just makes it all much easier.
The turning point is when a graph changes from increasing to decreasing, or the other way around. What this means is that its slope is changing from positive to negative, or the other way around.
The derivative allows you to find the slope at any point of a graph. If you are unfamiliar witht his concept let me know and I can go more into it.
Since the derrivative tells you the slope, if you find a spot where it equals 0 then you know before that point it was positive or negative, and then after that point it was the opposite. In other words it changes, so it's exactly what we are looking for. Also if a derrivative is ever non existant, like in the square root function the numbers under the square root cannot be negative, so any x value that makes them negative doesn't exist, this means you would want to check these point too because they can be turning points as well.
There are certain special cases where a derivative does not coss 0, and if that happens then the original function does not have a turning point. So keep that in mind.
The derivative is 3x^2 - 12. So we want to find when this equals 0. We also know it always exists so only need to worry about the 0s. Hopefully you are familiar with quadratics having two zeroes, if not let me know.
3x^2 - 12 = 0
3x^2 = 12
x^2 = 4
x = 2 and-2
So these are the turning points. You should double check though and choose an x value below -2, then between -2 and 2, then larger than 2 and make sure the signs swap.
These are the x values of the turning points. Solve f(x) at these points to find the y values. so f(-2) = (-2)^3 - 12(-2) + 5 = 21 and f(2) = -11 so now we know the turning points are (-2, 21) and (2, -11)
The coordinates of the turning points of f(x) are (-2, 21) and (2, -11).
What is differential equation?An equation containing derivatives of a variable with respect to some other variable quantity is called differential equations. The derivatives might be of any order, some terms might contain product of derivatives and the variable itself, or with derivatives themselves.
The turning point is when a graph changes from increasing to decreasing, or the other way around that means, its slope is changing from positive to negative.
Given that the derivative of f(x) = x³ – 12x + 5 is 3x² - 12.
Since the derrivative tells the slope, if you find a spot where it equals 0 then before that point it was positive or negative, and then after that point it was the opposite.
The derivative is 3x² - 12.
3x² - 12 = 0
3x² = 12
x² = 4
Thus, x = 2 and-2
So, these are the turning points.
Now Solve f(x) at these points to find the y values.
so f(x) = x³ – 12x + 5
f(-2) = (-2)³ - 12(-2) + 5 = 21
f(2) = -11
Hence, the coordinates of the turning points of f(x) are (-2, 21) and (2, -11).
Learn more about equations here;
https://brainly.com/question/25180086
#SPJ2
PLEASE SOMEONE HELP ME. I WILL BRAINLIEST YOU AND GIVE YOU POINTS.

Answers
Answer:
option D is the answer
Step-by-step explanation:
3n + 5
_______
n² + 5
f : x →x³- 2x + 1. Find:
a) f(2)
b) f(-2)
c) f(100)
d) f(0)
e) f(1/2)
Answers
Answer:
a) f(2) = 5
b) f(-2) = -3
c) f(100) = 999801
d) f(0) = 1
e) f(\(\frac{1}{2}\)) = \(\frac{1}{8}\)
Step-by-step explanation:





Pls help me it’s so hard imo thank you sm

Answers
Answer: 7e-5 millimeters, and the nanometer scale is more appropriate
Step-by-step explanation: PLEASE MARK ME BRAINLIEST!!!!!!
-divide the length value by 1e+6
-The millimeter scale and the centimeter scale are two huge, while the nanometer scale is too small. The nanometer scale is often used to measure atoms and viruses.
Answer:
a) The length of the virus in millimetres is 0.000 07 mm.
b) Viruses are microscopic and so nanometres are the more appropriate unit for writing the length of the virus since the nanometre is a smaller unit of measurement than the millimetre.
Step-by-step explanation:
SI is the abbreviation for The International System of Units.
The SI base unit for length is metres (m).
Milli and nano are SI prefixes used to form decimal multiples or submultiples of SI units.
1 millimetre (mm) = 1 × 10⁻³ metres = 0.001 m1 nanometre (nm) = 1 × 10⁻⁹ metres = 0.000 000 001 mTherefore, to convert nanometres to millimetres, multiply the nanometres by 10⁻⁶:
1 nm = 1 × 10⁻⁶ mmSo 70 nanometres is:
70 × 10⁻⁶ mm = 0.000 07 mmViruses are microscopic and so nanometres are the more appropriate unit for writing the length of the virus since the nanometre is a smaller unit of measurement than the millimetre.
Dr.Osborne has scheduled Anita Blanchette for a spirometry test and wants you to telephone her the day before the test to prepare her so that optimal results are obtained.
1.) What information do you give Anita before her spirometry so that the best test results can be obtained?
2.) How would you explain the rationale for the performance of this procedure?
Answers
To ensure the best test results, Anita should be provided with the following information before her spirometry:
1. Instructions for taking the test: Anita should be thoroughly explained about how the spirometry test works and what steps she needs to follow. This includes taking a deep breath and blowing as hard as she can into the spirometer mouthpiece. It is important to emphasize that she needs to repeat this procedure a few times and take deep breaths between each exhale.
2. Emphasize the importance of taking medication as prescribed: Anita should be reminded of the importance of taking her medications as prescribed, including on the day of the test. It is crucial for her to bring her medications to the test appointment.
3. Avoid certain foods and drinks: Anita should be informed to avoid consuming certain substances before the spirometry test, such as caffeine, alcohol, and heavy meals. These can potentially affect the accuracy of the test results.
4. Arrive early for the test: Anita should be advised to arrive early for the test to allow herself sufficient time to relax and calm down before the procedure. This can help ensure more accurate results.
The rationale behind providing these instructions and information is that spirometry is a lung function test that measures the amount and speed of air being breathed in and out. By following the instructions and guidelines, Anita can achieve optimal results, aiding in the diagnosis and assessment of lung conditions.
Learn more about spirometry and its significance in assessing lung function:
https://brainly.com/question/18155241
#SPJ11
Find y as a function of x if y‴−13y″+40y′=56e^x, y(0)=20, y′(0)=19, y″(0)=10.
Answers
The function y in the differential equation y‴−13y″+40y′=56eˣ, y(0)=20, y′(0)=19, y″(0)=10 as a function of x is: y(x) = -18 + e⁵ˣ + (9/32)e⁸ˣ + 2eˣ.
To solve this problem, we need to find the general solution to the differential equation y‴−13y″+40y′=56eˣ and then use the initial conditions to find the particular solution.
First, we find the characteristic equation:
r³ - 13r² + 40r = 0
Factorizing it, we get:
r(r² - 13r + 40) = 0
Solving for the roots, we get:
r = 0, 5, 8
So the general solution is:
y_h(x) = c1 + c2e⁵ˣ + c3e⁸ˣ
To find the particular solution, we can use the method of undetermined coefficients. Since the right-hand side of the differential equation is of the form keˣ, where k = 56, we assume a particular solution of the form:
y_p(x) = Aeˣ
Taking the first three derivatives:
y′_p(x) = Aeˣ
y″_p(x) = Aeˣ
y‴_p(x) = Aeˣ
Substituting these into the differential equation, we get:
Aeˣ - 13Aeˣ + 40Aeˣ = 56eˣ
Simplifying, we get:
28Aeˣ = 56eˣ
So A = 2. Substituting this value back into y_p(x), we get:
y_p(x) = 2eˣ
Therefore, the general solution is:
y(x) = y_h(x) + y_p(x)
= c1 + c2e⁵ˣ + c3e⁸ˣ + 2eˣ
Finding the values of the constants c1, c2, and c3:
y(0) = c1 + c2 + c3 + 2 = 20
y′(0) = 5c2 + 8c3 + 2 = 19
y″(0) = 25c2 + 64c3 = 10
Solving these equations simultaneously, we get:
c1 = -18
c2 = 1
c3 = 9/32
Therefore, the particular solution is:
y(x) = -18 + e⁵ˣ + (9/32)e⁸ˣ + 2eˣ
Know more about differential equation here:
https://brainly.com/question/14620493
#SPJ11
bob traveled 90 miles, which was 83 1/3% of his trip. How many miles did he still have to go
Answers
Bob will need to travell 18 miles more to complete his trip if he had travelled 90 miles before.
How can the distance that he will still travelled be calculated?The concept that will be used is the concept of percentage.
From the question, 83 1/3% of his journey has completed, then we need to calculate this and convert it to miles, which =0.833
The total distance will now be 90miles/0.833
= 108 miles
The remaining journey to complete his journey will now be [ (108) - (90)]= 18miles.
Hence, Bob will need to travel 18miles more.
Learn more about distance at:
https://brainly.com/question/17273444
#SPJ1
The area of a circle is 4π cm². What is the circumference, in centimeters? Express your answer in terms of π pie
Answers
Answer:
The formula for the area of a circle is:
A = πr^2
where A is the area and r is the radius.
In this case, we are given that the area is 4π cm². Solving for the radius, we get:
4π = πr^2
r^2 = 4
r = 2
So the radius of the circle is 2 cm.
The formula for the circumference of a circle is:
C = 2πr
Plugging in the value for the radius, we get:
C = 2π(2) = 4π
Therefore, the circumference of the circle is 4π cm.
what is the y-intercept of the function k(x)=3x^4 4x^3-36x^2-10
Answers
To find the y-intercept of the function k(x) = 3x^4 + 4x^3 - 36x^2 - 10, we evaluate the function at x = 0. The y-intercept is the point where the graph of the function intersects the y-axis. In this case, the y-intercept is -10.
The y-intercept of a function is the value of the function when x = 0. To find the y-intercept of the function k(x) = 3x^4 + 4x^3 - 36x^2 - 10, we substitute x = 0 into the function:
k(0) = 3(0)^4 + 4(0)^3 - 36(0)^2 - 10
= 0 + 0 - 0 - 10
= -10
Therefore, the y-intercept of the function is -10. This means that the graph of the function k(x) intersects the y-axis at the point (0, -10).
Learn more about y-intercept here:
https://brainly.com/question/14180189
#SPJ11
a math test consists of 10 multiple choice questions, each with four possible answers. if one guesses randomly, what is the probability of getting exactly 5 correct out of 10?
Answers
Therefore, the probability of getting exactly 5 correct out of 10 when guessing randomly is 0.2461.
This is a binomial probability problem, where each question is a trial with a probability of success (getting the correct answer) of 1/4, since there are four possible answers and only one is correct. We want to find the probability of getting exactly 5 correct out of 10, so the number of trials is n = 10 and the number of successes we want is k = 5.
The formula for the probability of getting k successes in n trials, each with a probability of success p, is:
P(k) = (n choose k) * p^k * (1-p)^(n-k)
where (n choose k) is the number of ways to choose k successes out of n trials, and is calculated as n! / (k! * (n-k)!).
Plugging in the values for this problem, we get:
P(5) = (10 choose 5) * (1/4)^5 * (3/4)^5
= (252) * (1/4)^5 * (3/4)^5
= 0.2461 (rounded to four decimal places)
To know more about probability,
https://brainly.com/question/30034780
#SPJ11
Solve the equation! 6(3c-5d+6)
Answers
Answer:
18c-30d+36
Step-by-step explanation:
A boy was asked to find LCM of 3,15,12 and another number. But while calculating, he
wrote 21, instead of 12 and yet the result came with the correct answer. What could be the
fourth number
Answers
The fourth number could be any multiple of 21, such as 42, 63, 84, and so on.
Least Common MultipleIf the boy calculated the least common multiple (LCM) of 3, 15, 21, and another number and still obtained the correct answer, it suggests that the fourth number is a multiple of 21.
The LCM of a set of numbers is the smallest number that is divisible by each number in the set without leaving a remainder. Since the LCM calculation with 21 resulted in the correct answer, it implies that the other numbers (3, 15, and 21) have a common multiple that is also divisible by the fourth number.
To find the fourth number, we need to consider the common multiples of 3, 15, and 21. The multiples of 3 are 3, 6, 9, 12, 15, 18, 21, and so on. The multiples of 15 are 15, 30, 45, 60, and so on. The multiples of 21 are 21, 42, 63, 84, and so on.
From these lists, we can observe that the common multiples of 3, 15, and 21 are numbers like 21, 42, 63, etc. Therefore, the fourth number could be any multiple of 21, such as 42, 63, 84, and so on.
More on least common multiple can be found here: https://brainly.com/question/30060162
#SPJ1
HELP ME PLS "A school is planning for an addition in some open space next to the current building. The existing building ends at the origin. The graph represents the system of equations that can be used to define the space for the addition. What is the system of equations that matches the graph?"

Answers
Answer:
y ≤ 3x
y > - 2x - 1
(1st choice)
Step-by-step explanation:
URGENT PLEASE!! I’ll give you brainliest! You just have to find x

Answers
Step-by-step explanation:
3(x+2)-(2x-1)=4(3-x)
3x+6-2x+1=12-4x
3x-2x+4x=12-6-1
5x=5
x=1
Answer:
x=1 2/5
Step-by-step explanation:
3x+6-2x-1=12-4x
x+5=12-4x
-5 -5
x=7-4x
+4x +4x
5x=7
/5 /5
x=7/5
x=1 2/5