#6Change from standard form to vertex formy=x²-8x+17
Answers
So the vector form of the quadratic function y = x² - 8x + 17 is: y = (x - 4)² + 1.
To change from standard form to vertex form, we need to complete the square.
First, we group the x-terms together and factor out any common coefficient of x², giving:
y = x² - 8x + 17
y = 1(x² - 8x) + 17
Next, we need to add and subtract a constant inside the parentheses to complete the square. To determine this constant, we take half of the coefficient of x (-8) and square it:
(-8/2)² = 16
So we add and subtract 16 inside the parentheses:
y = 1(x² - 8x + 16 - 16) + 17
Now we can factor the quadratic expression inside the parentheses as a perfect square:
y = 1[(x - 4)² - 16] + 17
Simplifying and rearranging terms, we get:
y = (x - 4)² + 1
To know more about vector,
https://brainly.com/question/20426452
#SPJ11
Related Questions
how many solutions does 4x+1=3x+2
one solution
no solution
infinitely many solutions
Answers
Answer:
one solution
Step-by-step explanation:
If you simplify the equation, it becomes 1x+1=2. Then you subtract the 1 from 2 and get 1x=1. Therefore, x=1 which is ONE SOLUTION.
i forgote what is 1+1= pls tell me
Answers
Answer:
two
Step-by-step explanation:
Rachel's water bottle holds 4 cups of water. How many times can she fill her water bottle from a 1-gallon jug of water?
Answers
Answer:
4 times
Step-by-step explanation:
there is 16 cups of water in a gallon
16/4=4
4 quarts = 8 pints
8 pints = 16 cups
So 1 gallon = 16 cups of water
12 1/2 − 9 1/4
This problem comes from subtract mixed numbers
5 3/4 - 2 5/12
7 1/5 - 3 7/10
11 2/3 - 8 1/2
Answers
12 1/2 = 2 * 12 + 1 = 25/2
9 1/4 = 4 * 9 + 1 = 37/4
Multiply 25/2 by 2/2 to have a common denominator:
25/2 * 2/2 = 50/4
50/4 - 37/4 = 13/4 or 4 1/3
Use the quadratic formula to find the exact solutions of x2 − 9x + 5 = 0.
x equals negative b plus or minus the square root of b squared minus 4 times a times c, all over 2 times a
Answers
Answer:
\(\frac{9\pm\sqrt{61}}{2}\)
Step-by-step explanation:
\(\displaystyle x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}=\frac{-(-9)\pm\sqrt{(-9)^2-4(1)(5)}}{2(1)}=\frac{9\pm\sqrt{81-20}}{2}\\\\=\frac{9\pm\sqrt{61}}{2}\)
The city plans a new road that will be parallel to Village Way and pass through the intersection of Gray Dr and Canon Rd. What is the equation of the road in slope-intercept form?

Answers
The equation line of the of the road in slope-intercept form is; y = 2·x - 10
What is the standard form of the equation of a line?The standard form of the equation of a line is Ax + Bx + C, where A, B, and C are constants and A and B are nonzero numbers.
The parameters for the new road are;
The road will be parallel to village way with points (0, 5), and (-4, -3)
The road will pass through the intersection of Gray Dr and Canon Rd., which is the point with coordinates (3, -4)
Required; The equation of the road
Since the new road is parallel to Village Way, which has slope;
m = (5 - (-3))/(0 - (-4)) = 8/4 = 2
The slope of the new road will also be 2.
Let the equation of the new road be y = m·x + c, where m = 2 is the slope we just found. To find c, we use the fact that the road passes through the point (3, -4);
y - (-4) = 2 × (x - 3)
y = 2·x - 6 - 4 = 2·x - 10
y = 2·x - 10
Therefore, c = -10
Therefore, the equation of the new road in slope-intercept form, therefore is; y = 2·x - 10
Learn more on the slope-intercept form of the equation of a line here: https://brainly.com/question/29283210
#SPJ1
solve the inequality 5x+3> 48
Answers
Answer:
x > 9
Step-by-step explanation:
for this inequality, we want to isolate x, so that we know the inequality of x
5x + 3 > 48
- 3 -3 {subtract 3 from both sides to get x alone}
5x > 45
/5 /5 {divide both sides by 5 to find 1x}
x > 9
So , x > 9 is the inequality in terms of x {is the solution}
hope this helps! :)
Answer:
\(\huge\boxed{\sf x > 9}\)
Step-by-step explanation:
Given inequality:5x + 3 > 48
Subtract 3 to both sides
5x > 48 - 3
5x > 45
Divide 5 to both sides
x > 9
\(\rule[225]{225}{2}\)
It's in the screenshot


Answers
The length of line segment A'B' is: D. 15 units.
Based on these transformations, the coordinates of the image of vertex Z are (-4, 3).
How to determine the length of line segment A'B'?By applying a dilation with a scale factor of 3/4 centered at the origin to line segment AB, we have the following:
Ordered pair A (4, 16) → Ordered pair A' (4 × 3/4, 16 × 3/4) = Ordered pair A' (3, 12).
Ordered pair B (20, 4) → Ordered pair B' (20 × 3/4, 4 × 3/4) = Ordered pair B' (15, 3).
Mathematically, the distance between two (2) points that are on a coordinate plane can be calculated by using this formula:
Distance A'B' = √[(x₂ - x₁)² + (y₂ - y₁)²]
Distance A'B' = √[(15 - 3)² + (3 - 12)²]
Distance A'B' = √[12² + 9²]
Distance A'B' = √[144 + 81]
Distance A'B' = √225
Distance A'B' = 15 units.
Question 2.By translating the pre-image of quadrilateral WXYZ vertically up by 4 units and horizontally right by 7 units, the coordinates of Z include the following:
(x, y) → (x + 7, y - 4)
Coordinate Z = (-3, 1) → Coordinate Z' = (-3 + 7, 1 - 4) = (4, -3)
Furthermore, the mapping rule for the rotation of a geometric figure about the origin by 180° is given by this mathematical expression:
(x, y) → (-x, -y)
Coordinate Z' = ((-4), -(-3)) = (-4, 3).
Read more on rotation here: brainly.com/question/28515054
#SPJ1
Factor
10x + 100x + 250
Answers
Is the answer
Suppose Joan has a fair four-sided die with sides that are numbered 1, 2, 3, and 4.
After she rolls it 20 times, how many times does she roll the number 3?
A. 3
B. 5
C. 6
D. It is impossible to tell.
Answers
To find the expected number of times Joan rolls a 3, we use the formula for mean of a binomial distribution.
The correct option is, option (C) 6.
The probability of rolling a number 3 on any given roll is 1/4
If Joan rolls the die 20 times, the number of times she rolls a 3 will follow a binomial distribution with n = 20 (number of trials) and p = 1/4 (probability of success).
The formula for the probability mass function of a binomial distribution is:
P(X=k) = (n choose k) * p^k * (1-p)^(n-k)
where X is the random variable representing the number of successes (the number of times Joan rolls a 3), k is the number of successes, n is the number of trials, p is the probability of success, and (n choose k) is the binomial coefficient, which represents the number of ways to choose k items from a set of n items.
Using this formula, we can calculate the probability of rolling a 3 exactly k times out of 20 rolls:
P(X=k) = (20 choose k) * (1/4)^k * (3/4)^(20-k)
To find the expected number of times Joan rolls a 3, we can use the formula for the mean of a binomial distribution:
E(X) = n * p
In this case, E(X) = 20 * 1/4 = 5
Therefore, the expected number of times Joan rolls a 3 is 5.
Since the possible answers are integers, the closest answer to 5 is 6. Therefore, the answer is (C) 6.
Know more about binomial distribution here:
https://brainly.com/question/29163389
#SPJ11
Two points located on JK are A-1,-9) and K(5,3). What is the slope of JK ?
OA -2
OB. -1/2
OC. 1/2
O D. 2
Answers
Answer:
D .2
Step-by-step explanation:
3-(-9)
5-(-1)
=3+9
5+1
12
6
= 2
Please help!! Find the value of x.
6
8
A
D
4
x = [?]
Enter
![Please help!! Find the value of x.68AD4x = [?]Enter](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/5Tv7c4JOKQcNg7qnxvtYvn6DtiR1MtCx.png)
Answers
Answer:
3
Step-by-step explanation:
By angle bisector property:
\( \frac{6}{x} = \frac{8}{4} \\ \\ \frac{6}{x} = 2 \\ \\ x = \frac{6}{2} \\ \\ x = 3\)
The value of given triangle of x is 3.
Angle bisector theorem states that an angle bisector of a triangle divides the opposite side into two segments that are proportional to the other two sides of the triangle. An angle bisector is a ray that divides a given angle into two angles of equal measures.
We have the given triangle is:
The triangle is ABC
and divide into two parts.
Triangle ADC and Triangle CBD.
The value also given in the figure.
AB = 6
BC = 8
AD = x
DC = 4
We have to find the value of x:
By using the Angle bisector theorem :
\(\frac{AB}{AD} =\frac{BC}{DC}\)
Plug all the values in above formula:
\(\frac{6}{x}=\frac{8}{4}\)
=> 6/x = 2
x = 6/2
x= 3
The value of given triangle of x is 3
Learn more about Angle bisector theorem at:
https://brainly.com/question/31330246
#SPJ2
Write 56% as a fraction in simplest form.
Answers
Answer:
\(\frac{14}{25}\)
Step-by-step explanation:
per cent means 'out of 100 ' , then
56%
= \(\frac{56}{100}\) ( divide numerator/ denominator by 4 )
= \(\frac{14}{25}\) ← in simplest form
Consider these functions:
f(x)=4x³-10
g(x)=3x-4/2
What Is the value of g(f(2))?
A. -6
B. 2
C. 19
D. 31

Answers
Answer:
i'm gonna say that its negitive 6 number one
Step-by-step explanation:
The value of g(f(2)) is 31 which correct option(D).
What is function?The function is defined as mathematics expression defines a relationship between one variable and another variable.
f(x) = 4x³-10
g(x) = 3x-4/2
Substitute value of f(x) in g(x),
\(g(f(x)) = \dfrac{3(4x^3-10) - 4}{2}\\g(f(x)) = \dfrac{12x^3-30 - 4}{2}\\g(f(x)) = \dfrac{12x^3-34}{2}\)
g(f(x)) = 6x³-17
Substitute x = 2,
g(f(2)) = 6(2)³-17
g(f(2)) = 6(8)-17
g(f(2)) = 31
Learn more about function here:
brainly.com/question/12431044
#SPJ5
help pls i didn't put the question fully on the last question:/
Find the decimal that is equivalent to: 17/12
A. 1.714
B. 0.583
C. 0.0583
D. 0.583 repeating
Answers
which of the following affect the width of a confidence interval? (select all that apply) group of answer choices mean standard deviation confidence level sample size
Answers
b) Decreasing the sample size
c) Increasing the standard deviation
a) Decreasing the confidence level will decrease the width of the confidence interval. A lower confidence level means we are less certain about capturing the true population mean, so we allow for a smaller margin of error, resulting in a narrower interval.
b) Decreasing the sample size will increase the width of the confidence interval. With a smaller sample size, there is less information available to estimate the population mean. This increased uncertainty leads to a wider confidence interval to accommodate a potentially larger margin of error.
c) Increasing the standard deviation will increase the width of the confidence interval. A larger standard deviation indicates more variability in the data. With greater variability, the estimated population mean could be further away from the true mean, requiring a wider interval to capture the potential range.
d) Decreasing the mean does not affect the width of the confidence interval. The width of the interval is primarily determined by factors such as confidence level, sample size, and standard deviation. The value of the population mean itself does not impact the width of the interval since it is the target value being estimated.
In summary, decreasing the confidence level and sample size, as well as increasing the standard deviation, will all increase the width of the confidence interval for a population mean, reflecting increased uncertainty and potential variability in the estimation. However, decreasing the mean does not directly impact the width of the interval.
Visit here to learn more about standard deviation:
brainly.com/question/29115611
#SPJ11
Graph the equation
y
=
x
2
−
12
x
+
35
y=x
2
−12x+35 on the accompanying set of axes. You must plot 5 points including the roots and the vertex.
Answers
X^2-12x+35=0
A=1 B=-12 C=35
B^2-4ac=(-12)^2 -4(1)(35)
=144 -140
=4
x=(-b+/- square root of b^2 -4ac) /over/ (2a)
Plug in the numbers
x=-(-12) sqr (-12)^2 4(1)(35) / (2)(1)
X=12 +/-sqr 4 / 2
Positive outcome
x=12 + sqr 4 / 2
x=12+2/2
x=7 <— this one
Negative outcome
x=12-2i/2
x=6-i
Vertex: (6,-1)
What is the answer for page 785 CPM textbook
Answers
Step-by-step explanation:
????????????........
Does 5, square root of 50, 5 make a right triangle?
Does square root of 2, square root of 3, 4 make a right triangle?
Answers
Answer:
A. Yes (True) B. Yes (True)
Step-by-step explanation:
The first some is true because the square root of 50 is between 6 and 7, which IS greater than 5
The second one is false because the square root of 3 is between 1 and 2, which which could be some of the a+v side of the triangle.
Hope this helped
show that tan(15 ) = 2 - rt3
Answers
By using trigonometry,
we have shown that tan(15°) = 2 - √3.
what is the trignometry?One of the most significant areas of mathematics, trigonometry has a wide range of applications. T
he study of the relationship between the sides and angles of the right-angle triangle is essentially the focus of the field of mathematics known as "trigonometry."
Hence, employing trigonometric formulas, functions, or trigonometric identities can be helpful in determining the missing or unknown angles or sides of a right triangle.
Angles in trigonometry can be expressed as either degrees or radians. 0°, 30°, 45°, 60°, and 90° are some of the trigonometric angles that are most frequently employed in computations.
We can use the half-angle formula for tangent to show that:
tan(15°) = tan(30°/2) = (1 - cos(30°)) / sin(30°)
We know that cos(30°) = √3/2 and sin(30°) = 1/2, so we can substitute those values in:
tan(15°) = (1 - √3/2) / 1/2
Simplifying the denominator and multiplying by the reciprocal:
tan(15°) = 2(1 - √3/2)
Simplifying the expression:
tan(15°) = 2 - √3
Therefore, we have shown that tan(15°) = 2 - √3.
To know more about trigonometry visit,
https://brainly.com/question/29002217
#SPJ1
Find the result of |x-1|=2
Answers
The absolute value of x minus one is equal to two. Therefore, x must be either one greater than two (x = 3) or one less than two (x = 1).
One less than x results in a value of two in absolute terms. As a result, x minus 1 has an absolute value of 2, which is a positive number. The separation of an integer from zero is its absolute value. As a result, x minus 1 is two units from zero in absolute terms. As x minus one has an absolute value of two, its real value must either be two or a negative two. That is to say, x must either be one more than two (x = 3) or one less than two (x = 1).In order to confirm this, let's look at a few examples. If x = 3, then |x - 1| = |2 - 1| = |1| = 1 which is not equal to two. Therefore, x = 3 is not the answer we are looking for. On the other hand, if x = 1, then |x - 1| = |1 - 1| = |0| = 0 which is not equal to two. Therefore, x = 1 is also not the answer we are looking for. The only two possible solutions for the equation |x - 1| = 2 are x = 3 and x = 1. Therefore, the result of |x - 1| = 2 is that x must be either one greater than two (x = 3) or one less than two (x = 1)
Learn more about absolute value here
https://brainly.com/question/1301718
#SPJ4
is the fraction 18/3 a rational number
Answers
Answer:
no it is not a rational number because
Step-by-step explanation:
183 is a fraction, which can be simplified as 618 13 =61=6 . Hence, It belongs to Natural numbers , which are {1,2,3,4,5,6...............}
Did you understand?
the correct answer is E
Answers
Answer:
its e lol
Step-by-step explanation:
Answer:
for what?
Step-by-step explanation:
Distance Conversions The United States, Liberia, and Myanmar are the only three countries that have not adopted the metric system as its primary system of measurement. There have been reports and legislation calling for a conversion to the metric system since the 1960s. The U.S. Department of Commerce's National Institute of Standards and Technology wrote that "industrial and commercial productivity, mathematics and science education, and the competitiveness of American products and services in world markets, will be enhanced by completing the change to the metric system of units" (1997, 2). From a student's perspective, it would be better if the U.S. converted to the metric system. Because scientists globally use the metric system, most of U.S. scientists do, as well. Until the U.S. "metrifies", students in the United States will need to continue to use and understand both measurement systems. 6. Refer to Appendix 2.1. Show your calculations for the following questions. 33 | Lab 2: Map Interpretation a. 2 miles contain how many feet? b. 1 mile contains how many inches? c. 10 kilometers contain how many meters? d. 1 kilometer contains how many centimeters? e. How many miles are in a "5k" (five-kilometer) race? f. A marathon is 26.2 miles. How many kilometers is this?
Answers
Answer:
a. 10560
b. 63360 in.
c. 10000 m
d. 100000 cm
e. 3.107 miles
f. 42.165 km
Step-by-step explanation:
a. 2 miles contain how many feet?
1 mile = 5280 ft
2 miles × 5280 ft / mile = 10560 ft
b. 1 mile contains how many inches?
1 ft = 12 in
1 mile × 5280 ft/mile × 12 in./ft = 63360 in.
c. 10 kilometers contain how many meters?
1 km = 1000 m
10 km × 1000 m/km = 10000 m
d. 1 kilometer contains how many centimeters?
1 km × 1000 m/km × 100 cm/m = 100000 cm
e. How many miles are in a "5k" (five-kilometer) race?
1 in. = 2.54 cm
5 km =
= 5 km × 1000 m/km × 100 cm/m × 1 in. / (2.54 cm) × 1 ft / (12 in.) × 1 mile / (5280 ft)
= 3.107 miles
f. A marathon is 26.2 miles. How many kilometers is this?
26.2 miles =
26.2 miles × 5280 ft / mile × 0.3048 m/ft × km / (1000 m) = 42.165 km
Which is the better buy on hamburger meat?
2 lbs. for $4.50
3 lbs. for $6.90
Click on the correct answer.
Answers
Answer:
2 lbs. for $4.50
Step-by-step explanation:
Do a ratio
2 : 4.50
You want to see how much it cost per pound, so divide them by 2
2 ÷ 2 : 4.50 ÷ 2
1 : 2.25
So per pound, the hamburger will cost $ 2.25
________________________________________________________
3 : 6.90
You want to see how much it cost per pound, so all you need to do is divide them by 3
3 ÷ 3 : 6.90 ÷ 3
1 : 2.3
So for the first one, it cost 2.25 per pound, and for the second one, it cost 2.3 per pound....the one that is better will be 2.25 because it cost 5 cents less than the second one
Hope this helped!
Have a supercalifragilisticexpialidocious day!
For f(x)=4x+1 and g(x)=x^2-5, find (g/f)(x)
Answers
Answer:
\((g/f)(x) = \frac{g(x)}{f(x)} = \frac{ {x}^{2} - 5 }{4x + 1} \)
I hope I helped you^_^
Draw the graph of each circle given its equation below.

Answers
Step 1:
First, write the general equation of a circle
\(\begin{gathered} (x-a)^a+(y-b)^2=r^2 \\ r\text{ is the radius} \\ (a,\text{ b) is the center} \end{gathered}\)Step 2:
Question 1
\(\begin{gathered} x^2+y^2\text{ = 121} \\ x^2+y^2=11^2 \\ \text{radius r = 11} \\ \text{center = (0 , 0)} \end{gathered}\)Question 2
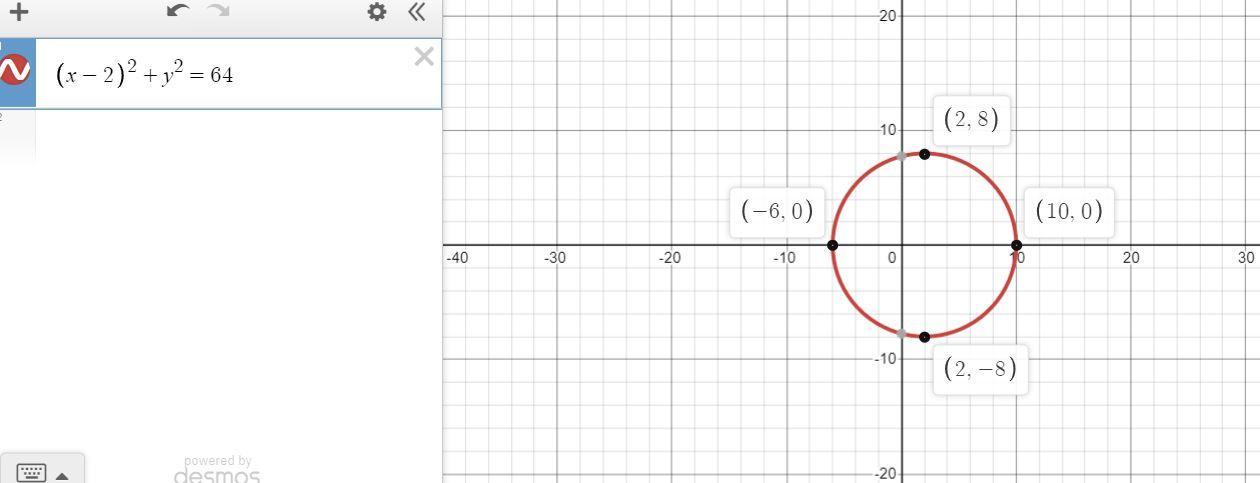
\(\begin{gathered} (x-2)^2+y^2\text{ = 64} \\ (x-2)^2+y^2=8^2 \\ \text{Center = (2, 0)} \\ r\text{ = 8} \end{gathered}\)Question 3
\(\begin{gathered} (x\text{ + }\frac{3}{2})^2\text{ + (y + }\frac{5}{8})^2\text{ = 36} \\ (x\text{ + }\frac{3}{2})^2\text{ + (y + }\frac{5}{8})^2\text{ = }6^2 \\ \text{Center = (-}\frac{3}{2}\text{ , -}\frac{5}{8}) \\ r\text{ = 6} \end{gathered}\)Question 4
\(\begin{gathered} (x-1)^2+(y+7)^2\text{ = 9} \\ (x-1)^2+(y+7)^2\text{ = }3^2 \\ \text{Center = (1, -7)} \\ r\text{ = 3} \end{gathered}\)Question 5
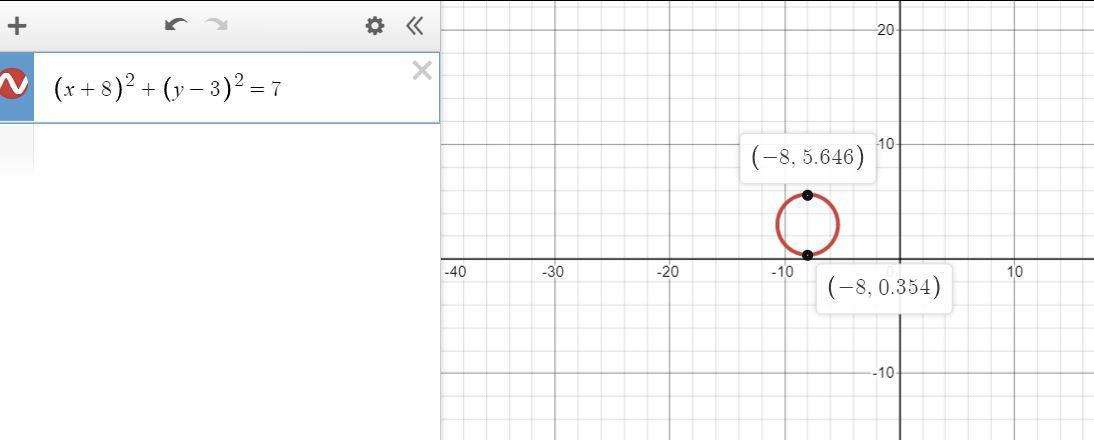
\(\begin{gathered} (x+8)^2+(y-3)^2\text{ = 7} \\ (x+8)^2+(y-3)^2\text{ = (}\sqrt[]{7})^2 \\ \text{Center = (-8, 3)} \\ \text{radius r = }\sqrt[]{7} \end{gathered}\)


consider the differential equation y '' − 2y ' 26y = 0; ex cos(5x), ex sin(5x), (−[infinity], [infinity]).Verify that the given functions form a fundamental set of solutions of the differential equation on the indicated interval
Answers
The given function satisfies the differential equation.Therefore, the given functions ex cos(5x) and ex sin(5x) form a fundamental set of solutions of the differential equation y'' - 2y' + 6y = 0 on the interval (−∞, ∞).
Given Differential Equation: y'' - 2y' + 6y
= 0Let's substitute the given function ex cos(5x) to the differential equation:y'' - 2y' + 6y
= 0 Differentiating y'' with respect to x:dy''/dx
= -25ex cos(5x) + 10ex sin(5x) dy''/dx
= (5.25) ex cos(5x) + 25ex sin(5x)Substituting these values, we get the following:y'' - 2y' + 6y
= (-25) ex cos(5x) + 10ex sin(5x) - 2(5ex sin(5x)) + 6ex cos(5x)
= (5.25ex cos(5x) + 25ex sin(5x)) - (10ex sin(5x) + 10ex sin(5x)) + 6ex cos(5x)
= ex cos(5x)(5.25 - 2 + 6) + ex sin(5x)(25 - 10 - 10)
= 9.25 ex cos(5x) + 5 ex sin(5x)The given function satisfies the differential equation.Now, let's substitute ex sin(5x) into the differential equation:y'' - 2y' + 6y
= 0 Differentiating y'' with respect to x:dy''/dx
= 25ex sin(5x) + 10ex cos(5x) dy''/dx
= (5.25) ex sin(5x) - 25ex cos(5x)Substituting these values, we get the following:y'' - 2y' + 6y
= (25) ex sin(5x) + 10ex cos(5x) - 2(25ex cos(5x)) + 6ex sin(5x)
= (5.25ex sin(5x) - 25ex cos(5x)) - (20ex cos(5x) - 10ex cos(5x)) + 6ex sin(5x)
= ex sin(5x)(5.25 + 6) + ex cos(5x)(10 - 20)
= 11.25 ex sin(5x) - 10 ex cos(5x).The given function satisfies the differential equation.Therefore, the given functions ex cos(5x) and ex sin(5x) form a fundamental set of solutions of the differential equation y'' - 2y' + 6y
= 0 on the interval (−∞, ∞).
To know more about fundamental visit:
https://brainly.com/question/32742251
#SPJ11
In the figure below, AB is a diameter of circle P.
What is the arc measure of major arc ABC in degrees?

Answers
Answer: 249
Step-by-step explanation: Khan Academy
Answer:
111
Step-by-step explanation:
GOT IT RIGHT!
ANSWER ASAP WILL GIVE BRAINLIEST
in the diagram below what is the approximate length of the minor arc ab
A 31.4
B 14.3
C 7.9
D 15.7
