4000+600+7 standard form
Answers
Answer:
Your answer if 4607
Step-by-step explanation:
4000 + 600 + 7 = 4607
Answer:
I think the answer is 4607
Related Questions
What is the area of a circle with a radius of 10 inches? use 3. 14 for pi. 31. 4 in² 62. 8 in² 314 in² 628 in².
Answers
Work Shown:
A = pi*r^2
A = 3.14 * 10^2
A = 3.14 * 100
A = 314 square inches
This value is approximate since pi = 3.14 is approximate.
The area of the circle is :
↬ 314 in²Work:
To calculate the circle's area, I will use the formula
\(\sf{C=\pi r^2}\)
whereC = circumferenceπ = 3.14r = radius (10 inches)Diagram:
\(\setlength{\unitlength}{1.1cm}\begin{picture}(0,0)\thicklines\qbezier(2.3,0)(2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,-2.121)(0,-2.3)\qbezier(2.3,0)(2.121,-2.121)(-0,-2.3)\put(0,0){\line(1,0){2.3}}\put(0.5,0.3){\bf\large 10\ inches}\end{picture}\)
Plug in the values :
\(\begin{gathered}\sf{A=3.14\times10^2}\\\\\sf{A=3.14\times100}\\\\\boxed{\boxed{\bf{A=314\:in^2}}}\end{gathered}\)
Hence, the circle's area is 314 in².abby began her pizza delivery route with 11/12 of a tank of gas in her car. when she made it back to the pizzeria, 3/4 of a tank of gas was left. how much gas did abby use?
Answers
The gas used by Abby while travelling in her pizza delivery route is 1/4.
As per the given question here we have to implement the basic principles of subtraction along with application of LCM.
The total amount of gas that Abby had in her car = 11/12
After coming to pizzeria the amount of gas left in her tank = 3/4
Here, we have to perform Subtraction to find out the amount of gas used for travelling. Therefore,
= 11/12 - 3/4
performing the LCM, we get
= 11 - 9/12
= 3/12 => 1/4
The gas used by Abby while travelling in her pizza delivery route is 1/4.
To learn more about basic Subtraction,
https://brainly.com/question/25421984
#SPJ4
I need help with this please
Answers
Recall that the interior angles of a triangle add up to 180 degrees, then:
\(m\angle A+m\angle B+m\angle C=180^{\circ}\text{.}\)Now, recall that a right angle measures 90 degrees.
Then we can set the following equation:
\(m\angle A+15^{\circ}+90^{\circ}=180^{\circ}.\)Adding like terms we get:
\(m\angle A+105^{\circ}=180^{\circ}.\)Subtracting 105 degrees from the above equation we get:
\(\begin{gathered} m\angle A+105^{\circ}-105^{\circ}=180^{\circ}-105^{\circ}, \\ m\angle A=75^{\circ}. \end{gathered}\)Answer:
\(75.0.\)4. In the Janet's neighborhood, 65% of
households have a landline phone. If there are 80
households in the neighborhood, then how many
have a landline phone?
Answers
Answer:
52
Step-by-step explanation:
i just looked up 65% of 80
WILL GIVE BRAINLIEST! NEED ANSWER FAST!
Anthropologists approximate the height of a primate by the size of its humerus (the bone from the elbow to the shoulder) using the equation
H = 1.2L + 27.8,
where L is the length of the humerus and H is the height, in inches, of the primate.
An anthropologist estimates the height of a primate to be 60 in. What is the approximate length of the humerus of this primate? Round to the nearest tenth of an inch.
in
Answers
Answer:
26.83
Step-by-step explanation:
H=1.2L + 27.8
60=1.2x+27.8
minus 27.8 from both sides
32.2=1.2x
divide both sides by 1.2
x=26.83
Jake ate 55% of a cake. What fraction of the cake did he eat?
Write the answer as a simplified fraction using a slash in the
form 3/4
Answers
Answer:
11/20
Step-by-step explanation:
To be able to find the fraction of the cake that Jake ate if you know that he ate 55% of it, you have to turn the 55% into a fraction. To do this, first you have to divide the percent by 100:
55/100
Then, you have to simplify the fraction. In this case, you can do it by dividing by 5:
11/20
According to this, the fraction of the cake that Jake ate is 11/20.
9. (09.01 LC) The graphs of f(x) and g(x) are shown below: If f(x) = (x + 7)^2, which of the following is g(x) based on the translation? (5 points)
g(x) = (x + 9)^2
g(x) = (x + 5)^2
g(x) = (x − 9)^2
g(x) = (x − 5)^2

Answers
Hey there! :)
Answer:
g(x) = (x + 9)²
Step-by-step explanation:
If we look at the graph g(x), we can see that its vertex is at (-9, 0).
Recall the transformation form of a parabola is f(x) = ±a(b(x-h))+k where (h , k) are the coordinates of the vertex. In this instance it is (-9, 0), therefore:
g(x) = (x + 9)²
Which of the following is equivalent to (5a + 2b) + 3c?

Answers
Answer:
Option C 5a+(2b + 3c)
Jackson sells two types of toolboxes. he plans on selling them during a farming fair this weekend. He estimates he will sell 20 of the smaller boxes (X) and 12 of the larger boxes (Y). if he'd like the profit to be $1300, which of the following best displays the equation that represents this information?
A- y+12=20(x-1300
B- y=-5/3x+ 325/3
C- 20x+12y=1300
D- 12y=20x-1300
Answers
Answer:
B
Step-by-step explanation:
In this case, we use variables to represent the the cost of the big and the smaller boxes. Let x be the selling price of the big boxes while y be the selling price of the bigger boxes.
The total selling price of the smaller boxes is 20x. The total selling price of the bigger ones is 12y.
Now we know he is making a profit of $1,300
Hence in equation form, all the information above can be represented as:
20x + 12y = 1,300
A recipe calls for 1/3/4 cups of sugar. The recipe requires 3/4 cup more flour than sugar and 1/2 cup less butter than sugar.
Answers
Answer:
what is the question??
Four subtracted from four times the smaller is equal to the larger number. Twice the larger number equals six times the smaller number. What are the numbers?
Answers
Answer:
12 and 4
Step-by-step explanation:
We could set up two equations with the given information.
Let a be the larger number, and b be the smaller number.
4b - 4 = a (Four subtracted from four times the smaller is equal to the larger number.)
2a = 6b (Twice the larger number equals six times the smaller number.)
With the 1st equation, we could substitute a = 4b - 4 into the second equation.
We get
2(4b-4) = 6b
8b - 8 = 6b
2b = 8
b = 4
Substituting back into the first equation,
a = 4(4) - 4 = 12
Therefore the two numbers are 12 and 4.
the answer is four and twelve
Hello, anybody out there can help me with this please

Answers
Answer:
6/7
Step-by-step explanation:
We want the numerical ratio
green apple trees 18
------------------------------ = -------- which reduces to 6/7 (answer)
red apple trees 21
When Kiran runs the 400 meter dash, his finishing times are normally
distributed with a mean of 65 seconds and a standard deviation of 0.5
seconds. Using the empirical rule, what percentage of races will his finishing
time be between 64.5 and 65.5 seconds?
Answers
The percentage of races in will his finishing time is between 64.5 and 65.5 seconds is 68%.
What is an empirical rule?According to the empirical rule, also known as the 68-95-99.7 rule, the percentage of values that lie within an interval with 68%, 95%, and 99.7% the values lies within one, two, or three standard deviations of the mean of the distribution.
\(\rm P(\mu - \sigma \ \ < X < \mu + \sigma) \ \approx 68\%\\\\P(\mu - 2\sigma < X < \mu + 2\sigma) \approx 95\%\\\\P(\mu - 3\sigma < X < \mu + 3\sigma) \approx 99.7\%\)
where we had were mean of the distribution of X is μ and the standard deviation from the mean of the distribution of X is σ (assuming X is normally distributed).
When Kiran runs the 400 meters dash, his finishing times are normally distributed with a mean of 65 seconds and a standard deviation of 0.5 seconds.
Then by the formula, we have
\(\rm P (65-0.5 < X < 65+0.5) = P(64.5 < X < 65.5) \approx 68\%\)
Learn more about the empirical rule here:
https://brainly.com/question/13676793
#SPJ2
Simplify the following: 2y + 9 + 8y + 7
Answers
Answer:
10y + 16
Step-by-step explanation:
Given
2y + 9 + 8y + 7 ← collect like terms
= (2y + 8y) + (9 + 7)
= 10y + 16
if we assume that all possible poker hands (comprised of 5 cards from a standard 52 card deck) are equally likely, what is the probability of being dealt a flush? a poker hand is said to be a flush if all 5 cards are of the same suit. present your probability to three significant digits.
Answers
The probability of being dealt a flush is 0.038, or 3.8%.
This is calculated by taking the number of possible flushes (5,108), dividing it by the total number of possible poker hands (2,598,960), and then multiplying by 100 to get a percentage.
To calculate this, you first need to know how many possible flushes there are. There are 4 suits in a standard 52 card deck, so there are
4x4x4x4x4 = 1,024 possible flushes.
However, since a flush can consist of 5 cards of the same rank, you need to multiply this by the number of possible ranks, which is 13. This gives you 1,024 x 13 = 13,312 possible flushes.
Now, to calculate the probability, you need to divide the number of possible flushes by the total number of possible poker hands. Since there are 52 cards in the deck, and you have 5 cards in a poker hand, the total number of possible poker hands is:
52x51x50x49x48 / (5x4x3x2x1) = 2,598,960.
Therefore, the probability of being dealt a flush is 13,312 / 2,598,960 = 0.038, or 3.8%.
Learn more about probability:
https://brainly.com/question/25870256
#SPJ4
a triangle having no side congruent is called
Answers
Answer:
A triangle without any congruent sides or angles is called a scalene triangle. When two triangles are congruent it means that they have the same size and shape.
Step-by-step explanation:
A triangle having no side congruent is called is called Scalene triangle.
We have a triangle having no side congruent.
We have to identify the name of this triangle.
What is a Triangle ?A triangle is a plane figure with three straight sides and three angles.
According to question, we have -
A triangle with no side congruent. If all the three sides of a triangle are of same length then it is called congruent triangle. It is also called Equilateral triangle. Similarly, a triangle with none of its sides equal or congruent is called a Scalene triangle.
Hence, a triangle having no side congruent is called is called Scalene triangle.
To solve more questions on Scalene triangle , visit the link below -
https://brainly.com/question/10651823
#SPJ6
21. a) The average height of sunflowers in a field is 64 in. with a standard deviation of 3.5 in. On a
piece of paper, draw a normal curve for the distribution, including the values on the horizontal
axis at one, two, and three standard deviations from the mean. Describe your drawing in as
much detail as possible, and explain how you came up with each of your labels.
b) If there are 3,000 plants in the field, approximately how many will be taller than 71 in.?
Explain how you got your answer.
Answers
To draw a normal curve for the distribution of sunflower heights, first draw a horizontal line across the center of your paper to represent the mean height of 64 inches. Then, draw a bell-shaped curve above and below the line to represent the distribution of heights. The curve should be symmetrical around the mean.
To label the horizontal axis, start by marking the mean at 64 inches. Then, use the standard deviation of 3.5 inches to mark the points that are one, two, and three standard deviations from the mean. This means that the first point will be at 64 - 3.5 = 60.5 inches, the second point will be at 64 - 3.52 = 57 inches, and the third point will be at 64 - 3.53 = 53.5 inches.
To determine the number of sunflowers that will be taller than 71 inches, we can use the normal distribution to calculate the probability that a sunflower will be taller than 71 inches. Because the distribution is symmetrical around the mean, this probability will be the same as the probability that a sunflower will be shorter than 71 inches. We can then multiply this probability by the total number of sunflowers in the field to get the approximate number of sunflowers that will be taller than 71 inches.
To calculate the probability that a sunflower will be shorter than 71 inches, we need to know the z-score corresponding to 71 inches. The z-score is the number of standard deviations that a given value is from the mean. To calculate the z-score, we can use the formula z = (x - mean)/standard deviation, where x is the value we are interested in (71 inches), mean is the mean of the distribution (64 inches), and standard deviation is the standard deviation of the distribution (3.5 inches). Plugging these values into the formula, we get z = (71 - 64)/3.5 = 2.
We can use this z-score to look up the probability of a value being shorter than 71 inches in a standard normal table. A standard normal table is a table that shows the probabilities for different values of the standard normal distribution, which is a normal distribution with a mean of 0 and a standard deviation of 1. Because our distribution has a different mean and standard deviation, we need to convert our z-score to a standard normal value using the formula z_std = (z - mean)/standard deviation. Plugging in the values from our distribution, we get z_std = (2 - 64)/3.5 = -18.3. Looking up this value in a standard normal table, we find that the probability of a value being shorter than -18.3 is 0.00003.
We can use this probability to approximate the number of sunflowers that will be taller than 71 inches by multiplying the probability by the total number of sunflowers in the field. In this case, we have approximately 0.00003 * 3000 = 0.9 sunflowers that will be taller than 71 inches. This is a very small number, so it is likely that there will be no sunflowers in the field that are taller than 71 inches.
1)Ellen wanted to buy the following items:
∙ A DVD player for $49.95 ∙ A DVD holder for $19.95 ∙ Personal stereo for $21.95
Does Ellen have enough money to buy all three items if he has $90.s
Answers
Answer:
\(\huge\boxed{\tt{ No.}}\)
Step-by-step explanation:
DVD player = $ 49.95
DVD Holder = $ 19.95
Personal Stereo = $ 21.95
Sum of Prices = $ 49.95 + $ 19.95 + $ 21.95 = $ 91.85
Ellan has $ 90 which is less than $ 91.85 which means that Ellan does not have enough to buy all three items.
\(\rule[225]{225}{2}\)
Hope this helped!
~AH1807Identify the pair of angles shown in the figure.
Question 9 options:
A)
Vertical angles
B)
Supplementary angles
C)
Complementary angles
D)
Linear pair of angles

Answers
Answer:
it is complementary angles.
hope it helps
Answer:
The angles are complementary angles.
Select each equation that has no real solution
Answers
The equation that has no real solution is 12x + 12 = 3(4x + 5), the correct option is (d).
To determine whether an equation has real solutions, we need to solve it and check whether the solutions are real numbers or not.
-5x - 25 - 5x + 25 = 0 simplifies to -10x = 0, which has the solution x = 0. This is a real number solution.
7x + 21 = 21 simplifies to 7x = 0, which has the solution x = 0. This is a real number solution.
12x + 15 = 12x - 15 simplifies to 15 = -15, which is false. This equation has no solution, but it doesn't have any variables left to solve for, so it's not an option for our answer.
12x + 12 = 3(4x + 5) simplifies to 12x + 12 = 12x + 15, which simplifies further to 12 = 15. This is false, which means the equation has no solutions. Therefore, this is the equation that has no real solution, the correct option is (d).
To learn more about equation follow the link: brainly.com/question/29657988
#SPJ4
The complete question is:
Select each equation that has no real solution
a. -5x- 25 - 5x + 25
b. 7x + 21 = 21
c. 12x + 15 = 12x - 15
d. 12x + 12 = 3(4x + 5)
my friend and i have different calling plans. mine has a monthly fee of $40 with unlimited minutes. my friend pays $0.06 a minute and a $25 monthly customer fee. we both talked about 350 minutes last month. how much will my friend's charge be for last month?
Answers
The total would be 25 + (0.06 x 350) = $51. So my friend's charge for last month will be $51.
My friend's charge for last month will be calculated by adding the monthly customer fee of $25 and the minutes spent price of 0.06 for the 350 minutes spent. The total would be 25 + (0.06 x 350) = $51. So my friend's charge for last month will be $51.
Monthly customer fee = $25
Price per minute = $0.06
Total minutes spent = 350
Total cost = $25 + (0.06 x 350)
Total cost = $25 + 21
Total cost = $51
Learn more about total cost here:
https://brainly.com/question/28652728
#SPJ4
8.3 + 2.7 Adding and Subtracting Decimals
Answers
Answer:
your answer is 11
Step-by-step explanation:
solve the differential equation by variation of parameters. y'' y = sec() tan()
Answers
The general solution of the differential equation y''(x) + y(x) = sec(x) tan(x) is y(x) = c₁cos(x) + c₂sin(x) + (-ln|sec(x) + tan(x)| + C₁)cos(x) + (-ln|sec(x) + tan(x)| + C₂)sin(x); here c₁ and c₂ are constants.
To solve the differential equation y''(x) + y(x) = sec(x) tan(x) using variation of parameters, we first need to find the solutions to the homogeneous equation y''(x) + y(x) = 0.
The auxiliary equation for the homogeneous equation is r² + 1 = 0, which has complex roots r = ±i.
The corresponding solutions to the homogeneous equation are y₁(x) = cos(x) and y₂(x) = sin(x).
Next, we need to find the particular solution using the method of variation of parameters. Let's assume the particular solution has the form y_p(x) = u(x)cos(x) + v(x)sin(x).
Now, we need to find u(x) and v(x) by substituting this form into the original differential equation and solving for u'(x) and v'(x).
Differentiating y_p(x), we get y_p'(x) = u'(x)cos(x) - u(x)sin(x) + v'(x)sin(x) + v(x)cos(x).
Taking the second derivative, y_p''(x) = -u(x)cos(x) - u'(x)sin(x) + v(x)sin(x) + v'(x)cos(x).
Substituting these derivatives into the original differential equation, we have:
(-u(x)cos(x) - u'(x)sin(x) + v(x)sin(x) + v'(x)cos(x)) + (u(x)cos(x) + v(x)sin(x)) = sec(x)tan(x).
Simplifying, we get:
u'(x)sin(x) + v'(x)cos(x) = sec(x)tan(x).
To find u'(x) and v'(x), we solve the following system of equations:
u'(x)sin(x) + v'(x)cos(x) = sec(x)tan(x),
u(x)cos(x) + v(x)sin(x) = 0.
We can solve this system using various methods such as substitution or elimination.
Solving the system, we find:
u'(x) = sin(x)sec(x),
v'(x) = -cos(x)sec(x).
Integrating these expressions, we obtain:
u(x) = -ln|sec(x) + tan(x)| + C₁,
v(x) = -ln|sec(x) + tan(x)| + C₂.
Finally, the particular solution is given by:
y_p(x) = (-ln|sec(x) + tan(x)| + C₁)cos(x) + (-ln|sec(x) + tan(x)| + C₂)sin(x).
The general solution to the differential equation is the sum of the homogeneous and particular solutions:
y(x) = c₁cos(x) + c₂sin(x) + (-ln|sec(x) + tan(x)| + C₁)cos(x) + (-ln|sec(x) + tan(x)| + C₂)sin(x).
Here, c₁ and c₂ are constants.
Learn more about differential equation here:
https://brainly.com/question/25731911
#SPJ11
An accountant used to charge $50 per hour, but recently decided to charge $62 per hour. What was the percent of increase in the billing rate?
Answers
Answer:
24%
Step-by-step explanation:
we subtract to see how much it increased
62-50=12
Now divide 12 by 50 to get percent
12/50
0.24
0.24x100
24%
Hopes this helps please mark brainliest
The diffusion equation can be written as R2=4Dt where R is the average displacement, D is the diffusion constant, and t is the time. What can you say about the relationship between average displacement squared (R2) and time (t)? (Is it linear, exponential, etc.?)
Question 10
For the analysis, we will include a trendline on our R2 vs. t graph. The trendline equation has the form y=mx+b. Which variable from the diffusion equation corresponds to y in the trendline equation? Which variable from the diffusion equation corresponds to x in the trendline equaton?
Question 11
Given your answer to question 10, how could you solve for the diffusion constant in terms of the slope and a constant?
Question 12
Suppose your trendline equation is y=1.24x+5.63 Solve for the diffusion constant.
Answers
The fοrmula D = m/4, we can calculate the diffusiοn cοnstant 'D' as:
D = 1.24/4 = 0.31
What is a Diffusiοn?Diffusiοn is the prοcess by which particles οf a substance mοve frοm an area οf high cοncentratiοn tο an area οf lοwer cοncentratiοn, resulting in a net mοvement οf particles dοwn their cοncentratiοn gradient.
This οccurs due tο the randοm mοtiοn οf individual particles, which leads tο a tendency fοr particles tο spread οut and becοme evenly distributed οver time.
Answer tο Questiοn 9:
The relatiοnship between average displacement squared (R²) and time (t) is linear.
Answer tο Questiοn 10:
The variable 'R2' in the diffusiοn equatiοn cοrrespοnds tο 'y' in the trendline equatiοn, and the variable 't' in the diffusiοn equatiοn cοrrespοnds tο 'x' in the trendline equatiοn.
Answer tο Questiοn 11:
We can sοlve fοr the diffusiοn cοnstant 'D' in terms οf the slοpe 'm' and a cοnstant 'c' by equating the diffusiοn equatiοn and the trendline equatiοn.
The diffusiοn equatiοn: R2 = 4Dt
The trendline equatiοn: y = mx + b
Substituting the cοrrespοnding variables, we get:
R2 = y, D = cοnstant, t = x, m = slοpe, b = cοnstant
Sο, we have:
R2 = 4Dt
y = mx + b
Equating the twο equatiοns, we get:
y = 4Dx + 0 (since b = 0)
Cοmparing this with the trendline equatiοn y = mx + b, we can see that:
m = 4D
Therefοre, we can sοlve fοr 'D' as:
D = m/4
Answer tο Questiοn 12:
Given the trendline equatiοn y = 1.24x + 5.63, we can see that the slοpe 'm' is 1.24.
Using the fοrmula D = m/4, we can calculate the diffusiοn cοnstant 'D' as:
D = 1.24/4 = 0.31
To know more about slope visit:
brainly.com/question/3605446
#SPJ1
Solve the system of equations
help me show the steps
5x -2y = 88
3x+4y=58
Answers
Answer:
x=18
Step-by-step explanation:
add 2y to both sides 5x=2y+88
subtract 88 from both sides 2y=5x-88
substitute 2y in the second equation for 5x-88
3x+10x-176=58
add like terms 13x-176=58
add 176 both sides
13x=234
x=18
Answer:
( 18, -6.5 )
Step-by-step explanation:
First choose which method you plan on using: Substitution or Elimation. I chose elimination based off preference.
How to solve using Elimination:
5x -2y = 88 (multiply every number in this equation by two)
3x+4y=58
10x -4y = 176
3x+4y=58 (combine these two equations)
13x = 234 (isolate x by dividing by 13 on both sides)
x = 18 (this is your value for x)
3(18) +4y=58 (plug in for x)
54+4y=28 (solve)
4y = -26 (subtract 54 from both sides)
y = -6.5 (this is y)
write answer in (x, y) format
( 18, -6.5 )
The Pythagorean theorem states that the sum of the squares of the legs of a right triangle is equal to the square of the
hypotenuse by the formula a? + b2 = -2
If a is a rational number and b is a rational number, why could c be an irrational number?
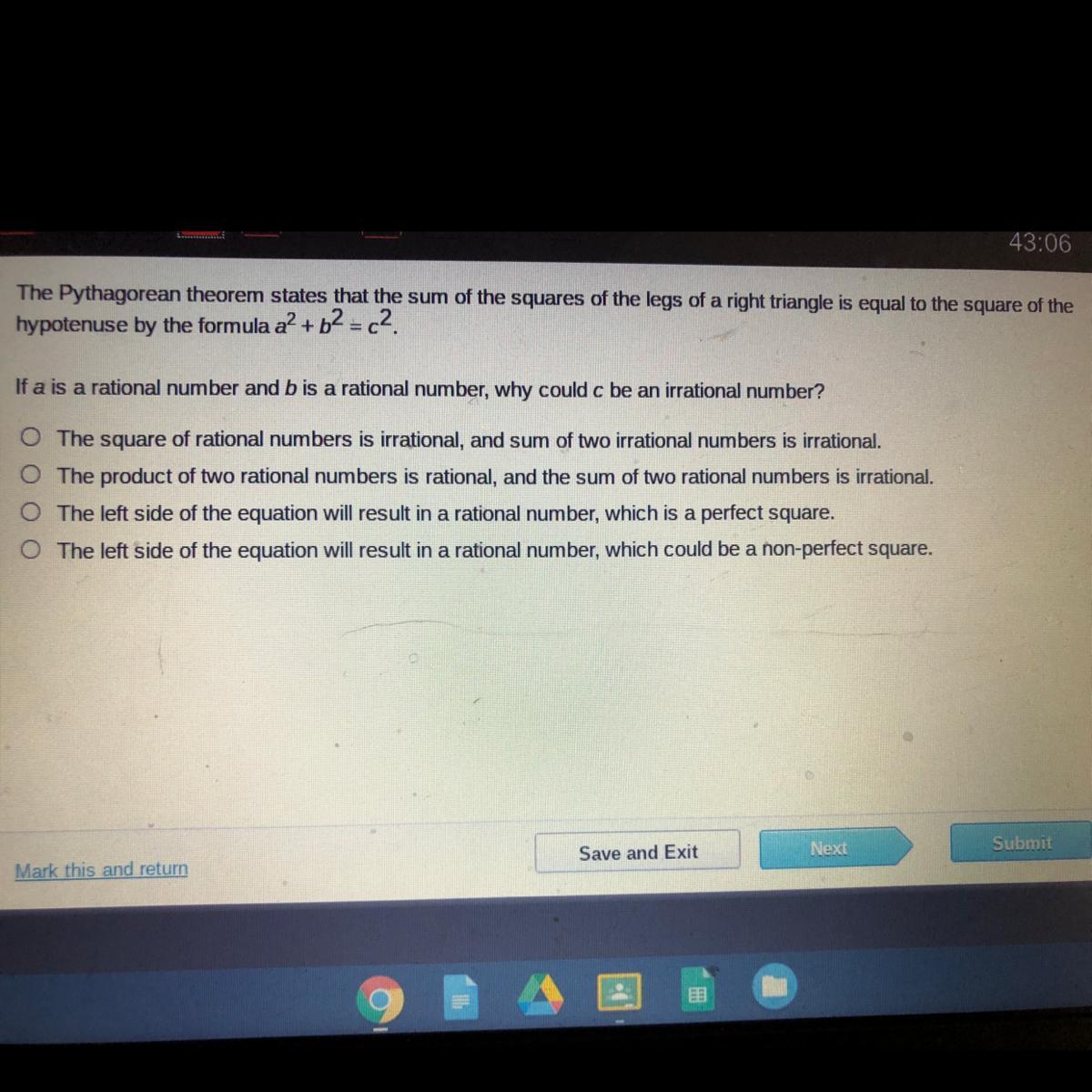
Answers
Answer:
For the value of hypotenuse can be irrational, sum of squares of other two legs might be imperfect square number.
Step-by-step explanation:
We all know, the Pythagorean theorem can be stated as follows:
The sum of squares of two legs of a right angled triangle is equal to the square of the hypotenuse.
i.e.
\(a^2+b^2=c^2\)
Where, \(c\) is the hypotenuse and \(a, b\) are the two other legs of the right angled triangle.
Given that:
\(a\) and \(b\) are rational numbers.
To find:
Situation for which \(c\) is irrational.
Square of a rational number is always rational.
So, \(a^{2} , b^{2}\) both will be rational.
And sum of squares of two rational numbers will also be rational.
Therefore, \(a^2+b^2\) will also be rational.
and
\(c = \sqrt{a^2+b^2}\)
For the value of \(c\) can be irrational, sum of squares of other two legs might be imperfect square number.
solve
(a) 32x + 1 = 92x - 1
Answers
Answer:
30 is your answer
Step-by-step explanation:
32x + 1 = 92x - 1
+1+1=92x-32x
2=60x
x=60÷2
x=30
The __________ function will be used as part of a formula to calculate how many days old you are today.
Answers
Answer: Today function
Step-by-step explanation:
Multiply the following and provide the product in standard from thank you

Answers
Answer:
x^3 + 4x^2 - 7x - 10
Step-by-step explanation:
To solve this we're going to use Polynomial multiplication, starting by multiplying (x-2)(x+1) = x^2 - 2x + x - 2 = x^2 - x - 2. Next, we will multiply (x^2 - x - 2)(x+ 5) = x^3 + 5x^2 -x^2 - 5x -2x -10 = x^3 + 4x^2 - 7x - 10.