3 1/18 As a decimal
No links or I’m blocking and reporting you :)
Answers
Answer:
\(3.0\overline{5}=3.0555555...\)
Step-by-step explanation:
We know that \(1/18=1/2*1/9=1/2*0.1111....=0.05555555...\).
So, \(3~1/18=3+0.055555555...=3.05555555=\boxed{3.0\overline{5}}\) and we're done!
Related Questions
Circle D is below. ⌢
What is the arc measure of BC in degrees
Answers
Answer:
\(BC = 84\)
Step-by-step explanation:
Given
See attachment
Required
Find BC
The sum of \(angles\ at\ a\ point\) is 360.
So:
\(7n + 12 + 13n - 16 + 6n = 360\)
Collect like terms
\(7n + 13n + 6n = 360 + 16 - 12\)
\(26n = 364\)
Solve for n
\(n = 364/26\)
\(n = 14\)
From the circle:
\(BC = 6n\)
Substitute 14 for n
\(BC = 6*14\)
\(BC = 84\)

A car travels 2 5/8
miles in 3 1/2
minutes at a constant speed. Which equation represents the distance, d, that the car travels in m minutes?
Ad = 0.75m
B. d=14 m
C. d = 3.5m
D. d = 2.625m

Answers
Answer:
A. d = 0.75m.
Step-by-step explanation:
If, for 3 1/2 minutes (3.5 minutes) the car travels 2 5/8 miles (2.625 miles),
Then in m minutes the car will travel d miles
d = (2.625*m)÷ 3.5
d = 0.75m
Which is option A
The ACT is a standardized test that many high school students in the U.S. take in order to apply for college (the other major admissions test is the SAT). The purpose of any standardized admissions test is to allow the institution at which the student is applying to predict how a student would perform academically, as measured by grade point average (GPA). Of course, many other criteria are considered by admissions committees, such as high school GPA and involvement in extracurricular activities, but we won't get into those here.
The dean of a college of business at a medium-sized regional university is interested in examining the relationship between ACT scores and GPAs of students in the college. After taking a random sample of 141 students, he performs a regression analysis using Excel and gets the output below:
Regression Statistics Multiple R 0.206754254 R Square 0.042747321 Adjusted R Square 0.035860611 Standard Error 0.365573763 Observations 141 ANOVA df SS MS F Significance F Regression 1 0.829558763 0.829559 6.20722 0.013899275 Residual 139 18.57654053 0.133644 Total 140 19.40609929 Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 2.402979486 0.264202725 9.095211 8.8E-16 1.880603742 2.925355229
ACT 0.027063973 0.01086283 2.491429 0.013899 0.005586227 0.048541719
The dean wants to create a 95% confidence interval for the mean GPA of students who have an ACT score of x0 = 13. What is the upper bound of this interval, to two decimal places?
You will need to use the fact that the average ACT scoretop enclose x equalsis 19.8, with a standard deviation of 4.3. Use three decimal places for all calculations up to the answer.
Hint: Use the confidence interval formula, not the prediction interval formula. The two formulas are very similar, but the confidence interval formula leaves off the "1+" under the square root.
Answers
the upper bound of the confidence interval is 3.09 (rounded to two decimal places).
To create a 95% confidence interval for the mean GPA of students who have an ACT score of x0 = 13, we first need to calculate the standard error of the mean:
SE = sqrt(MSE/n + (x0 - xbar)^2 / ((n-1)*Sx^2))
where:
MSE = mean square error from the ANOVA table = 0.133644
n = sample size = 141
x0 = ACT score of interest = 13
xbar = average ACT score = 19.8
Sx = standard deviation of ACT scores = 4.3
Plugging in the values, we get:
SE = sqrt(0.133644/141 + (13-19.8)^2 / ((141-1)*4.3^2)) = 0.155
Next, we calculate the t-value for a 95% confidence interval with 139 degrees of freedom (n-1):
t = 1.977
Finally, we can calculate the confidence interval using the formula:
CI = y0 ± t*SE
where:
y0 = predicted mean GPA for x0 = b0 + b1*x0, where b0 and b1 are the intercept and slope coefficients from the regression output
Plugging in the values, we get:
y0 = 2.402979486 + 0.027063973*13 = 2.788779395
CI = 2.788779395 ± 1.977*0.155 = (2.485, 3.092)
To know more about interval visit:
brainly.com/question/11051767
#SPJ11
Enter the letter of the graphed function.
a. y = (x + 2)(x - 1)³(x-3)
b. y = (x + 2)(x - 1)(x-3)³
c. y = (x + 2)(x - 1)²(x - 3)²
d. y = (x - 1)(x-3)²(x + 2)²
e. y = (x + 2)²(x-1)²(x-3)
10

Answers
Answer:
d. y = (x - 1)(x-3)²(x + 2)²
Step-by-step explanation:
When there is a local max or local min on the x-intercept, then the function on the x-intercept is raised to an even power.
At x=3 and x=-2, the function goes up then down, or down then up.
If the function goes through an x-intercept when there is no local max or local min on the x-intercept, then the function on the x-intercept is raised to an odd power.
At x=1, the function goes through the x-intercept.
Hence, d is the answer.
layla buys 3.6 pounds of dried fruit. the dried fruit costs $4.55 per pound. layla wants to know the total cost of the fruit.
Answers
Given:
Layla buys 3.6 pounds of dried fruit.
Cost of dried fruit is $4.55 per pound.
Cost per pound is multiplied to the number of pounds we buy.
\(\begin{gathered} \text{Total cost of the fruit }=3.6\times4.55 \\ =\text{ \$}16.38 \end{gathered}\)Name a pair of the supplementary angles
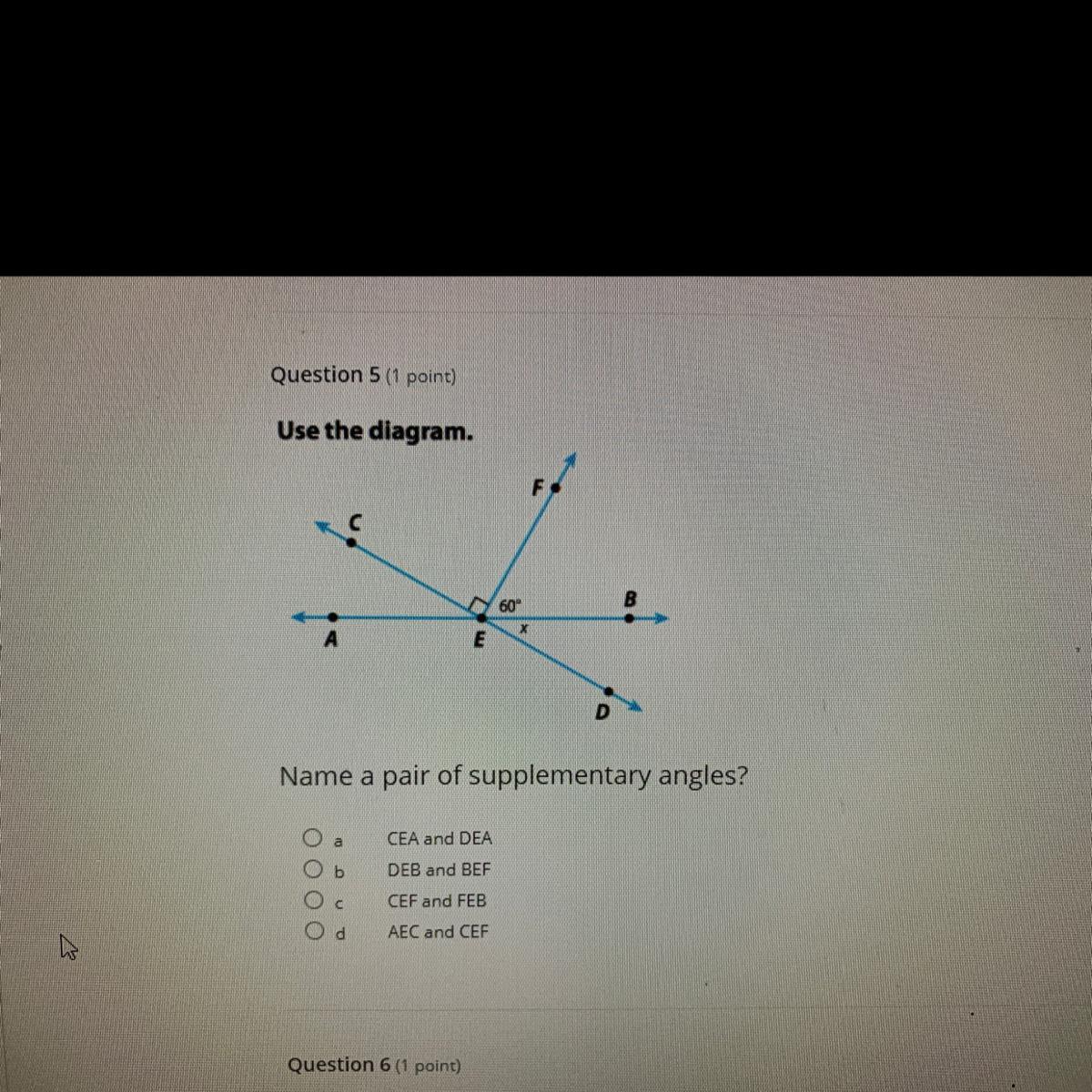
Answers
Answer:
a.CEA AND DEA
is pair of the supplementary angles
what is the slope of the line containing points (1,-3) and (4,2)
Answers
Answer:
5/3 is the slope
Step-by-step explanation:
Characterize the slope of the line in the graph.
© A. Negative
B. Zero
O O O O
C. Undefined
D. Positive
Answers
A.Negativ
#Keep on learning#Study hardPls can someone answer these two I will give brainliest and 30 points

Answers
Answer:
The first one is false.
3(2 ÷ x)
The second is true.
how many numbers must be randomly selected from the set \{1,3,5,7,9,11,13,15\}{1,3,5,7,9,11,13,15} to guarantee that at least one pair of these numbers add up to 1616?
Answers
The number of pairs that must be randomly selected from the set {1,3,5,7,9,11,13,15} to guarantee that at least one pair of these numbers add up to 16 is 5.
In the given set {1,3,5,7,9,11,13,15}, there are four pairs that sum up to 16, which are (1,15), (3,13), (5,11), and (7,9). Let k numbers be picked from the set. Consider k = 5, then using the pigeonhole principle, for one of the pairs described above, both of the endpoints must have been picked. Hence, if 5 numbers are picked from the set, then there exists a pair with a sum of 16.
To learn more about the pigeonhole principle and probability theorem,
https://brainly.com/question/24491336
#SPJ4
solve for brainliest

Answers
The students' Landry and Erika was the name used and the image is attached
What is linear function ?A linear function consists of functions where the variables has exponents of 1.
The graph of linear functions is a straight line graph and the relationship is expressed in the form.
y = mx + c
y = output variable
m = slope
x = input variable
c = y intercept
The two graphs shown the first from the left represents a positive slope while the second is a negative slope
Cole and Erika are both positive slopes while Landry has a negative slope. This makes Landry to be sure of the second graph
Considering c (y intercept)
In Cole's equation c = -1 and in Erika's equation c = +4
Erika's equation coincides with the graph with positive slope and Landry matches with second graph.
Learn more about graphs of linear functions at:
https://brainly.com/question/29244324
#SPJ1

guys please help me i need this done NOW

Answers
Answer:
see down
Step-by-step explanation:
10. a one to one function means only one input goes to the same output,
this one is not a one to one function, because there is 2 out put for each input except vertx
50 = -2.5x all u have to do is SOLVE
Answers
Answer: The answer is x = -20.
Answer:
x = -20
Step-by-step explanation:
50 = -2.5x
Divide both sides by -2.5
-20 = x
Suppose that 8 short range rockets of one kind have a mean target error of x₁ = 98 metres with a standard deviation of s₁ = 18 metres while 10 rockets of another kind have a mean target error of x₂ = 76 with standard deviation of s₂ = 15 metres. Assume that the target errors for the two types of rockets are normally distributed and that they have a common variance. Find the p-value of the test. O 0.2 O 0.1 O 0.5 O 0.4 O 0.3
Answers
Therefore, the p-value of the test is approximately 0.3.
To calculate the p-value, we will use the two-sample t-test. The null hypothesis (H₀) states that there is no difference in the mean target errors between the two types of rockets. The alternative hypothesis (H₁) states that there is a difference.
We can calculate the test statistic using the formula:
t = (x₁ - x₂) / √[(s₁²/n₁) + (s₂²/n₂)]
where x₁ and x₂ are the sample means, s₁ and s₂ are the sample standard deviations, and n₁ and n₂ are the sample sizes.
Plugging in the given values, we have:
x₁ = 98, s₁ = 18, n₁ = 8
x₂ = 76, s₂ = 15, n₂ = 10
Calculating the test statistic, we get:
t = (98 - 76) / √[(18²/8) + (15²/10)]
= 22 / √(36 + 22.5)
= 22 / √58.5
≈ 2.83
The p-value of the test can then be determined by comparing the test statistic to the t-distribution with (n₁ + n₂ - 2) degrees of freedom. In this case, since the p-value is not provided, we cannot determine its exact value. However, based on the given options, the closest value to 2.83 is 0.3.
Therefore, the p-value of the test is approximately 0.3.
To learn more about p-value visit:
brainly.com/question/30461126
#SPJ11
Please help asap will give brainliest. Find X and bac

Answers
By using the fact that the two angles whose measures are expressed in terms of x are vertical angles, we will see that x = 8.
Then using that we will see that the measure of angle BAC is 63 degrees.
How to find the value of x?On the given diagram, we can see that the two angles whose measures are expressed in terms of x are vertical angles, thus, these two angles have the same measure, then we can write a linear equation that helps us to find the value of x, which is:
(2x + 3) = (4x - 5)
Solving the linear equation for x we get:
2x + 3 = 4x - 5
3 + 5 = 4x - 2x
8 = 2x
8/2 = x = 4
So we can see that the value of x is 4.
Now we want to find the measure of angle BAC.
We can see that the measure of angle BAC plus the measure of the angle to its right will be a right angle, then we can write:
m∠BAC + (4x - 5)° = 90°
Replacing the value of x we get:
m∠BAC + (4*8 - 5)° = 90°
m∠BAC + 27° = 90°
m∠BAC = 90° - 27° = 63°
We conclude that the measure of angle BAC is 63 degrees.
If you want to learn more about vertical angles:
https://brainly.com/question/14362353
#SPJ1
How did you know that ordered pair satisfies the linear inequality in two variables?
Answers
Using the values provided in the ordered pair, The linear inequality is satisfied by putting the ordered pair values and checking if the statement is true or false.
What do you mean by a ordered pair?An ordered pair is made up of the ordinate and the abscissa of the x coordinate, with two values given in parenthesis in a certain sequence.
What is linear inequality?When two mathematical statements or two numbers are compared in an unequal way, it is known as an inequality in mathematics. Inequalities can generally be classified as either algebraic or numerical, or as a combination of the two.
ordered pair=(1,2)
linear inequality equation,
\(4x_{1}-x_{2} > 0\)
using value from ordered pair,
\(4*1 - 2 > 0\)
\(2 > 0\)
which is true. That is it satisfies the given linear inequality.
To learn more about inequality visit:
https://brainly.com/question/20383699
#SPJ4
explain how you determined which distribution to use. the t-distribution will be used because the samples are independent and the population standard deviation is not known. the standard normal distribution will be used because the samples are independent and the population standard deviation is known
Answers
You must use the t-distribution table when working problems when the population standard deviation (σ) is not known and the sample size is small (n<30). General Correct Rule: If σ is not known, then using t-distribution is correct. If σ is known, then using the normal distribution is correct.
What is t-distribution and normal distribution ?Normal distribution, also known as the Gaussian distribution, is a probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean.
In graphical form, the normal distribution appears as a "bell curve".
The normal distribution is the proper term for a probability bell curve.
In a normal distribution the mean is zero and the standard deviation is1. It has zero skew and a kurtosis of 3.
Normal distributions are symmetrical, but not all symmetrical distributions are normal.
The t-distribution describes the standardized distances of sample means to the population mean when the population standard deviation is not known, and the observations come from a normally distributed population.
Therefore,
You must use the t-distribution table when working problems when the population standard deviation (σ) is not known and the sample size is small (n<30). General Correct Rule: If σ is not known, then using t-distribution is correct. If σ is known, then using the normal distribution is correct.
Learn more about t-distribution and normal distribution here ;
https://brainly.com/question/24277447
#SPJ4
6.
The Solia family has a large garden that is 20 m by 14 m. They want to put in
a circular spa pool in a corner of the garden, as shown in the diagram.
3 m
3 m
Answers
Answer:
Am sorry but I think you forgot to add the photo of the diagram so please edit your question
(Trigonometry)Find the exact values of sin x/2, and tan x/2 if sin 5/13 and x is in Q2.
Answers
The exact value of sin(x/2) is (sqrt(1 - cos x) )/2 and the exact value of tan(x/2) is sin x / (1 + cos x), where x is the angle in radians.
Given that sin x = 5/13 and x is in the second quadrant, we can use the Pythagorean identity to find cos x. We have:
sin^2 x + cos^2 x = 1
Substituting sin x = 5/13, we get:
(5/13)^2 + cos^2 x = 1
Solving for cos x, we get:
cos x = -12/13
Now we can substitute cos x = -12/13 into the formulas for sin(x/2) and tan(x/2) to get:
sin(x/2) = sqrt(1 - cos x)/2 = sqrt(1 + 12/13)/2 = sqrt(25/26)/2 = (5/2)sqrt(2/13)
tan(x/2) = sin x / (1 + cos x) = (5/13) / (1 - 12/13) = -5
Therefore, the exact values of sin(x/2) and tan(x/2) are (5/2)sqrt(2/13) and -5, respectively.
To learn more about radians click here
brainly.com/question/7721249
#SPJ11
We can use the half-angle formulas to find the exact values of sin x/2 and tan x/2. In this case, we have:
sin(x/2) = ±√[(1 - cos x) / 2]
tan(x/2) = sin x / (1 + cos x)
First, we need to find cos x, since it is not given directly. We know that x is in quadrant 2, which means that the sine is positive and the cosine is negative. We can use the Pythagorean identity to find cos x:
sin^2 x + cos^2 x = 1
cos^2 x = 1 - sin^2 x
cos x = -√(1 - sin^2 x)
Plugging in sin x = 5/13, we get:
cos x = -√(1 - (5/13)^2) = -12/13
Now we can use the half-angle formulas:
sin(x/2) = ±√[(1 - cos x) / 2]
sin(x/2) = ±√[(1 + 12/13) / 2]
sin(x/2) = ±√(25/26)
Since x is in quadrant 2, we know that sin x/2 is positive. Therefore, we have:
sin(x/2) = √(25/26) = 5/√26
Next, we can use the formula for tangent:
tan(x/2) = sin x / (1 + cos x)
tan(x/2) = (5/13) / (1 - 12/13)
tan(x/2) = (5/13) / (1/13)
tan(x/2) = 5
Therefore, the exact values of sin x/2 and tan x/2 are:
sin(x/2) = 5/√26
tan(x/2) = 5
Learn more about half-angle formulas here : brainly.com/question/11911877
#SPJ11
A chess player ran a simulation twice to estimate the proportion of wins to expect using a new game strategy. Each time, the simulation ran a trial of 1,000 games. The first simulation returned 212 wins, and the second simulation returned 235 wins. Construct and interpret 95% confidence intervals for the outcomes of each simulation.
A. The confidence interval from the first simulation is (0.187, 0.237), and the confidence interval from the second simulation is (0.209, 0.261). For the first trial, we are 95% confident the true proportion of wins with the new game strategy is between 0.187 and 0.237. For the second trial, we are 95% confident the true proportion of wins with the new game strategy is between 0.209 and 0.261.
B. The confidence interval from the first simulation is (0.187, 0.237), and the confidence interval from the second simulation is (0.209, 0.261). For the first trial, we are 90% confident the true proportion of wins with the new game strategy is between 0.187 and 0.237. For the second trial, we are 90% confident the true proportion of wins with the new game strategy is between 0.209 and 0.261.
C. The confidence interval from the first simulation is (0.191, 0.233), and the confidence interval from the second simulation is (0.213, 0.257). For the first trial, we are 95% confident the true proportion of wins with the new game strategy is between 0.191 and 0.233. For the second trial, we are 95% confident the true proportion of wins with the new game strategy is between 0.213 and 0.257.
D. The confidence interval from the first simulation is (0.191, 0.233), and the confidence interval from the second simulation is (0.213, 0.257). For the first trial, we are 90% confident the true proportion of wins with the new game strategy is between 0.191 and 0.233. For the second trial, we are 90% confident the true proportion of wins with the new game strategy is between 0.213 and 0.257.
Answers
The correct option regarding the 95% confidence interval for this problem is given as follows:
A. The confidence interval from the first simulation is (0.187, 0.237), and the confidence interval from the second simulation is (0.209, 0.261). For the first trial, we are 95% confident the true proportion of wins with the new game strategy is between 0.187 and 0.237. For the second trial, we are 95% confident the true proportion of wins with the new game strategy is between 0.209 and 0.261.
What is a confidence interval of proportions?A confidence interval of proportions has the bounds given by the rule presented as follows:
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which the variables used to calculated these bounds are listed as follows:
\(\pi\) is the sample proportion, which is also the estimate of the parameter.z is the critical value.n is the sample size.The confidence level is of 95%, hence the critical value z is the value of Z that has a p-value of \(\frac{1+0.95}{2} = 0.975\), so the critical value is z = 1.96.
The parameters for the first simulation are given as follows:
\(n = 1000, \pi = \frac{212}{1000} = 0.212\)
Hence the lower bound of the interval is of:
\(0.212 - 1.96\sqrt{\frac{0.212(0.788)}{1000}} = 0.187\)
The upper bound is of:
\(0.212 + 1.96\sqrt{\frac{0.212(0.788)}{1000}} = 0.237\)
For the second simulation, the parameters are given as follows:
\(n = 1000, \pi = \frac{235}{1000} = 0.235\)
Hence the lower bound of the interval is of:
\(0.235 - 1.96\sqrt{\frac{0.235(0.765)}{1000}} = 0.209\)
The upper bound is of:
\(0.235 + 1.96\sqrt{\frac{0.235(0.765)}{1000}} = 0.261\)
This means that option A is the correct option.
More can be learned about the z-distribution at https://brainly.com/question/25890103
#SPJ1
the distribution of heights for adult men in a certain population is approximately normal with mean 70 inches and standard deviation 4 inches. which of the following represents the middle 80 percent of the heights? responses 50 inches to 73.37 inches 50 inches to 73.37 inches 62 inches to 78 inches 62 inches to 78 inches 64.87 inches to 75.13 inches 64.87 inches to 75.13 inches 66 inches to 74 inches 66 inches to 74 inches 66.63 inches to 90 inches
Answers
The correct answer is 64.87 inches to 75.13 inches.
To find the middle 80 percent of heights, we need to find the values of x that correspond to the 10th and 90th percentiles of the normal distribution with mean 70 inches and standard deviation 4 inches.
Using a standard normal table or calculator, we can find that the z-score corresponding to the 10th percentile is -1.28 and the z-score corresponding to the 90th percentile is 1.28.
So,
x = μ + zσ
x1 = 70 + (-1.28)(4) = 64.88
x2 = 70 + (1.28)(4) = 75.12
Therefore, the middle 80 percent of heights is between 64.88 inches and 75.12 inches, or approximately 64.87 inches to 75.13 inches.
To learn more about normal distribution, click here: brainly.com/question/4079902
#SPJ11
13 less than b In algebraic expression
Answers
13 less than b as an algebraic expression would be \(b - 13\).
This is because 13 less than a number is the same as that number being subtracted by 13. Let me know if you have any questions, thanks!
The function
�
ff is given in three equivalent forms.
Which form most quickly reveals the
�
yy-intercept?
Choose 1 answer:
Choose 1 answer:
(Choice A)
�
(
�
)
=
−
3
(
�
−
2
)
2
+
27
f(x)=−3(x−2)
2
+27f, left parenthesis, x, right parenthesis, equals, minus, 3, left parenthesis, x, minus, 2, right parenthesis, squared, plus, 27
A
�
(
�
)
=
−
3
(
�
−
2
)
2
+
27
f(x)=−3(x−2)
2
+27f, left parenthesis, x, right parenthesis, equals, minus, 3, left parenthesis, x, minus, 2, right parenthesis, squared, plus, 27
(Choice B)
�
(
�
)
=
−
3
�
2
+
12
�
+
15
f(x)=−3x
2
+12x+15f, left parenthesis, x, right parenthesis, equals, minus, 3, x, squared, plus, 12, x, plus, 15
B
�
(
�
)
=
−
3
�
2
+
12
�
+
15
f(x)=−3x
2
+12x+15f, left parenthesis, x, right parenthesis, equals, minus, 3, x, squared, plus, 12, x, plus, 15
(Choice C)
�
(
�
)
=
−
3
(
�
+
1
)
(
�
−
5
)
f(x)=−3(x+1)(x−5)f, left parenthesis, x, right parenthesis, equals, minus, 3, left parenthesis, x, plus, 1, right parenthesis, left parenthesis, x, minus, 5, right parenthesis
C
�
(
�
)
=
−
3
(
�
+
1
)
(
�
−
5
)
f(x)=−3(x+1)(x−5)f, left parenthesis, x, right parenthesis, equals, minus, 3, left parenthesis, x, plus, 1, right parenthesis, left parenthesis, x, minus, 5, right parenthesis
What is the
�
yy-intercept?
Answers
The constant term in the quadratic expression gives the y-intercept, which is 15 in this case.
The correct answer to the given question is option B.
The function ff is given in three equivalent forms, and we need to choose the form that most quickly reveals the y-intercept. We know that the y-intercept is the value of f(x) when x=0. Let's evaluate the function for x=0 in each of the given forms.
A. f(x)=−3(x−2)2+27
f(0)=−3(0−2)2+27=−3(4)+27=15
B. f(x)=−3x2+12x+15
f(0)=−3(0)2+12(0)+15=15
C. f(x)=−3(x+1)(x−5)
f(0)=−3(0+1)(0−5)=15
Therefore, we can see that all three forms give the same y-intercept, which is 15. However, form B is the quickest way to determine the y-intercept, since we don't need to perform any calculations. The constant term in the quadratic expression gives the y-intercept, which is 15 in this case. Hence, option B is the correct answer.
For more such questions on quadratic expression, click on:
https://brainly.com/question/11776031
#SPJ8
Write a 6-digit number that when rounded to the nearest thousand and hundred will have a result that is the same. explain
Answers
The 6 - digit number when rounded to the nearest thousand and hundred will have a result that is the 556100.
Rounding off makes a number is made simpler by keeping its value intact but closer to the next number.
Rounding to the nearest thousand:
The original number, 555500, lies between 555000 and 556000.
Since it is equidistant from both, we round it to the nearest even thousand, which is 556000.
Rounding to the nearest hundred:
The rounded number from the previous step, 556000, lies between 555900 and 556100.
Again, it is equidistant from both, but in this case, we round it up to the nearest hundred, which is 556100.
Therefore, when you round the number 555500 to the nearest thousand and hundred, you get the same result, which is 556100.
Thus, the answer is 556100.
Learn more about round off here :
https://brainly.com/question/28128444
#SPJ4
Please help ASAP!!!!!!

Answers
Answer:
Step-by-step explanation:
1. 15
2. 40
what is the unit rate for 4 gallons
Answers
Answer:
completing the division operation: numerator divided by denominator.
Step-by-step explanation:
If you have a rate, such as price per some number of items, and the quantity in the denominator is not 1, you can calculate unit rate or price per unit by completing the division operation: numerator divided by denominator.
i. The uniform probability distribution's shape is a rectangle. ii. The uniform probability distribution is symmetric about the mode. iii. In a uniform probability distribution, P(x) is constant between the distribution's minimum and maximum values. Multiple Choice (ii) and, (iii) are correct statements but not (i). (i). (ii), and (iii) are all false statements. (i) is a correct statement but not (ii) or (iii). (i) and, (iii) are correct statements but not (ii).
Answers
The correct option is: (i) and (iii) are correct statements but not (ii).
The correct answer is:
(i) The uniform probability distribution's shape is a rectangle.
(ii) The uniform probability distribution is symmetric about the mode.
(iii) In a uniform probability distribution, P(x) is constant between the distribution's minimum and maximum values.
Therefore, the correct option is: (i) and (iii) are correct statements but not (ii).
To know more about "Probability" refer here:
brainly.com/question/30034780#
#SPJ4
A new coffee shop can hold no more than 50 seats. The owner wants at least 20 of the seats to be stools and the remaining seats to be recliners. If x is the number of stools and y is the number of recliners, which graph represents the solution to the system of inequalities?
x + y ≤ 50
x ≥ 20
On a coordinate plane, 2 solid straight lines are shown. The first line is horizontal to the y-axis at y = 20. Everything below the line is shaded. The second line has a negative slope and goes through (0, 50) and (50, 0). Everything to the left of the line is shaded.
On a coordinate plane, 2 solid straight lines are shown. The first line is vertical to the x-axis at x = 20. Everything to the left of the line is shaded. The second line has a negative slope and goes through (0, 50) and (50, 0). Everything to the right of the line is shaded.
On a coordinate plane, 2 solid straight lines are shown. The first line is horizontal to the y-axis at y = 20. Everything above the line is shaded. The second line has a negative slope and goes through (0, 50) and (50, 0). Everything to the left of the line is shaded.
On a coordinate plane, 2 solid straight lines are shown. The first line is vertical to the x-axis at x = 20. Everything to the right of the line is shaded. The second line has a negative slope and goes through (0, 50) and (50, 0). Everything to the left of the line is shaded.
Answers
This region is below the line \(x + y = 50\) and to the left of the line \(x = 20,\) which is exactly what the first graph shows.
What is equation?The correct graph that represents the solution to the system of inequalities is the first one:
On a coordinate plane, 2 solid straight lines are shown. The first line is horizontal to the y-axis at y = 20. Everything below the line is shaded. The second line has a negative slope and goes through (0, 50) and (50, 0). Everything to the left of the line is shaded.
This is because the first inequality, \(x + y ≤ 50\) , represents the fact that the total number of seats \((x + y)\) cannot exceed 50. This means that the solution must lie below the line \(x + y = 50\) , which has a negative slope.
The second inequality, \(x ≥ 20\) , means that there must be at least 20 stools, which corresponds to a horizontal line at y = 20. Therefore, the solution must lie to the left of the line \(x = 20\).
Therefore, these two inequalities determine a shaded region that satisfies both conditions. This region is below the line \(x + y = 50\) and to the left of the line \(x = 20\) , which is exactly what the first graph shows.
Learn more about equation here:
https://brainly.com/question/10413253
#SPJ1
Define convenience purchases, shopping purchases, and specialty purchases. Describe three specific brand name products in the consumer marketplace today that would correspond to these three types of purchases.
Answers
Convenience purchase: Coca-Cola. Shopping purchase: Apple iPhone. Specialty purchase: Rolex. These brand name products correspond to their respective purchase types based on convenience, shopping involvement, and specialty appeal in the consumer marketplace.
Convenience purchases refer to low-involvement purchases made by consumers for everyday items that are readily available and require minimal effort to obtain. These purchases are typically driven by convenience and habit rather than extensive consideration or brand loyalty.
Shopping purchases involve higher involvement and more deliberate decision-making. Consumers invest time and effort in comparing options, seeking the best value or quality, and may consider multiple brands before making a purchase. These purchases often involve durable goods or products that require more consideration.
Specialty purchases are distinct and unique purchases that cater to specific interests, preferences, or hobbies. These purchases are driven by passion, expertise, and a desire for premium or specialized products. Consumers are often willing to invest more in these purchases due to their unique features, quality, or exclusivity.
Three specific brand name products in the consumer marketplace that correspond to these types of purchases are
Convenience Purchase: Coca-Cola (Soft Drink)
Coca-Cola is a widely recognized brand in the beverage industry. It is readily available in various sizes and formats, making it a convenient choice for consumers seeking a refreshing drink on the go.
With its widespread availability and strong brand presence, consumers often make convenience purchases of Coca-Cola without much thought or consideration.
Shopping Purchase: Apple iPhone (Smartphone)
The Apple iPhone is a popular choice for consumers when it comes to shopping purchases. People invest time researching and comparing features, pricing, and user reviews before making a decision.
The shopping process involves considering various smartphone brands and models to ensure they select a product that meets their specific needs and preferences.
Specialty Purchase: Rolex (Luxury Watches)
Rolex is a well-known brand in the luxury watch industry and represents specialty purchases. These watches are associated with high-quality craftsmanship, precision, and exclusivity.
Consumers who are passionate about luxury watches and seek a premium product often consider Rolex due to its reputation, heritage, and unique features. The decision to purchase a Rolex involves a significant investment and is driven by the desire for a prestigious timepiece.
These examples illustrate how different types of purchases align with specific brand name products in the consumer marketplace, ranging from convenience-driven choices to more involved shopping decisions and specialty purchases driven by passion and exclusivity.
To know more about Convenience purchases:
https://brainly.com/question/30247858
#SPJ4
Suppose a survey of 580 women in the United States found that more than 64% are the primary investor in their household. Which part of the survey represents the descriptive branch of statistics? Make an inference based on the results of the survey.64% of women in the sample are the primary investor in their household.
There is an association between U.S. women and being the primary investor in their household.
Answers
The sentence "64% of women in the sample are the principal investor in their household" serves as an example of descriptive statistics.
What will the inference be?This sentence provides a summary of the survey's data and a descriptive statistic (percentage) that characterizes the sample's characteristics.
According to the survey's findings, "there is a correlation between American women and being the principal investor in their household." The sample data are used to draw this conclusion about the population. Despite the fact that the sample is not representative of all American women, the findings indicate that a sizable number of the women in the sample are the principal investors in their households.
Learn more about Surveys here:
brainly.com/question/13532910
#SPJ4