28 = 3x – 7x + 4
Check:
Answers
Answer:
x= -6
Step-by-step explanation:
28=3x - 7x + 4
Combine Like Terms:
28= -4x + 4
Subract four from both sides (in order to isolate the variable):
24= -4x
Divide by -4 from both sides:
x= -6
Answer:
x= -6
Step-by-step explanation:
1. Subtract the x's
28 = -4x + 4
2. Subtract the 4 by both sides
(28 - 4) = -4x + (4-4)
3. Solve
24 = -4x
4. Divide Both sides by -4
24/-4 = -4/-4 x
5. Solve
-6 = x or x = -6
Related Questions
i do not know this answer
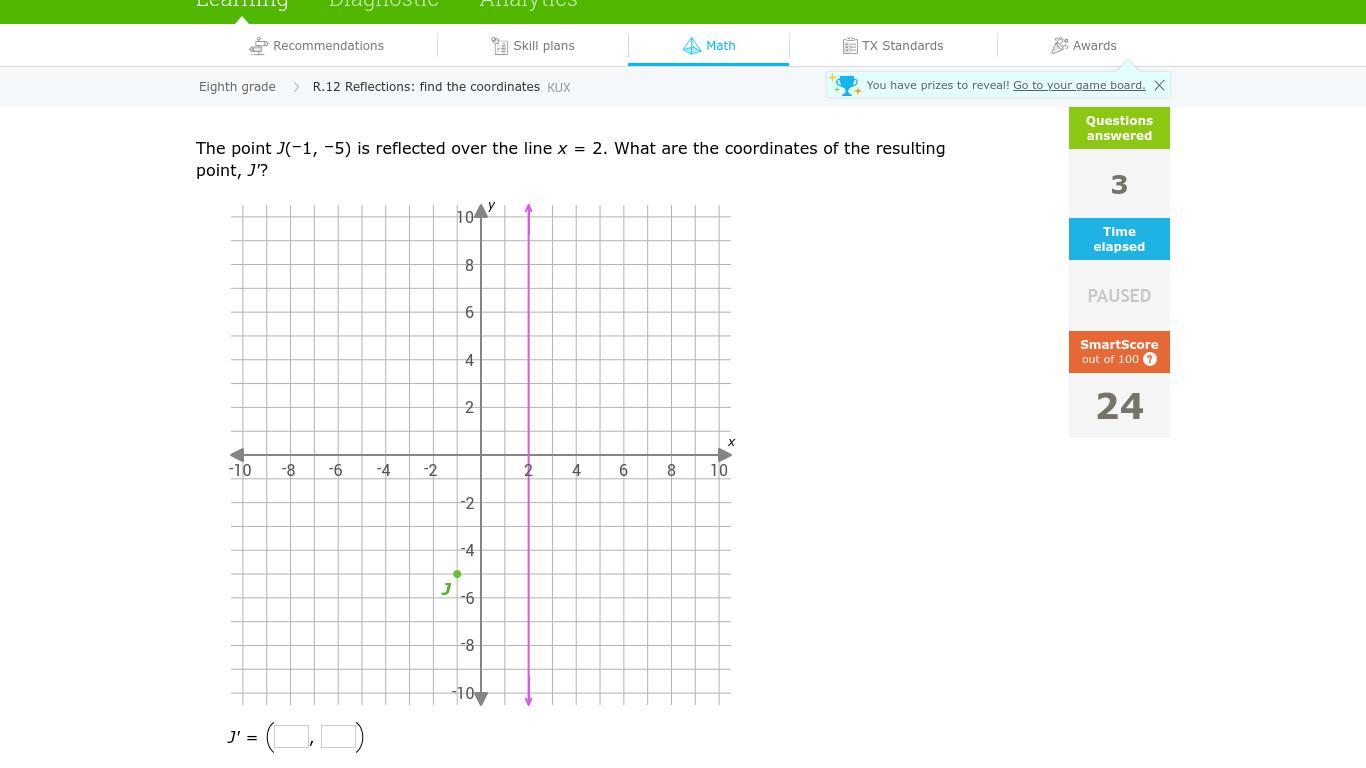
Answers
Answer:
(5, -5)
Step-by-step explanation:
The point J is 3 away form the line. so when reflected, it will be 3 away on the other side, thus (5, -5)
If 492 people choose to watch the fireworks from the castle and this is 76% of the people who watch the fireworks at all, how many people watch the fireworks altogether?

Answers
Using percentages the number of people is who watch the fireworks is 647.
What is a percentage?A percentage is a ratio out of hundred.
Since we have 492 people who choose to watch the fireworks from the castle and this is 76% of the people who watch the fireworks at all, how many people watch the fireworks altogether?
Now, percentage = number/total × 100 %
Now, we require the total number. Making the total number subject of the formula, we have that
total = number × 100 %/percentage
Since
number = 492 and percentage = 76 %So, substituting the values of the variables into the equation, we have that
total = number × 100 %/percentage
total = 492 × 100 %/76%
= 6.474 × 100 %
= 647.4
≅ 647
So, the number of people is 647.
Learn more about percentages here:
https://brainly.com/question/28757188
#SPJ1
Please solve this I'll give you 25 points

Answers
If I were to make a quick guess I think this is the line y=4X

Answer:
its linear (i know how to draw the graph but i cant show you here, just make umm an x axis and y axis from 1 to 30 ) (also i feel like theres another way to know if its linear but this is how i would do it!)
Step-by-step explanation:
to see if its linear ummm we first have to find the slope, the equation for the slope is
y2 - y1 / x2 - x1
lets use the points (2, 8) and (3, 12)
12 - 8/ 3 -2
4 / 1
4
y = 4x + b
now to find the y-intercept lets input a point we did not use yet
(5, 20)
20 = 4(5) + b
20 = 20 + b
b = 0
y = 4x
now we check if its linear with the points (6, 24) and (3.5, 14) sooo
24 = 4(6) ?
24 = 24
14 = 4(3.5) ?
14 = 14
so yes it is a linear graph
What is the speed of 240 km in 3 hours?
Answers
The speed of the moving body that is being referred to here is 80 kilometer per hour.
The given problem is a straightforward one based on the idea of the universal law of motion. According to the universal law of motion, any uniformly traveling body's distance traveled is determined by the product of its speed and the time elapsed. Distance is calculated as speed * time. Therefore the body is going at a speed of 80 kilometers per hour, according to the same relation as above, assuming that it is moving at a constant speed.
\(Distance = speed * time\)
Learn more about universal law of motion here:
https://brainly.com/question/21806184
#SPJ4
Classified ads in a newspaper offered for sale 20 used cars of the same make and model. The output of a regression analysis is given. Assume all conditions for regression have been satisfied. Create a 95% confidence interval for the slope of the regression line and explain what your interval means in context. Find the 95% confldence interval for the slope. The confidence interval is (Round to two decimal places as needed.)
Answers
Confidence interval refers to a statistical measure that helps quantify the amount of uncertainty present in a sample's estimate of a population parameter.
This measure expresses the degree of confidence in the estimated interval that can be calculated from a given set of data. In this scenario, the task is to build a 95% confidence interval for the regression line's slope. The regression analysis output has already been given. According to the output given, the estimated regression model is:y = 25,000 + 9,000 x, where x represents the number of miles the car has been driven and y represents the car's selling price.
The formula to calculate the 95% confidence interval for the slope is:Slope ± t · SE, where Slope is the point estimate for the slope, t represents the critical t-value for a given level of confidence and degrees of freedom, and SE represents the standard error of the estimate. The value of t can be calculated using the degrees of freedom and a t-table. Here, the number of pairs in the sample size is 20, and the model uses two parameters.
Therefore, the degrees of freedom would be 20 - 2 = 18.The critical t-value for a 95% confidence interval and 18 degrees of freedom is 2.101. Using the formula given above, we can calculate the 95% confidence interval for the slope as follows:Slope ± t · SE= 9000 ± (2.101)(700) ≈ 9000 ± 1,467.7 = [7,532.3, 10,467.7]Therefore, the 95% confidence interval for the slope is [7,532.3, 10,467.7]. This means that we are 95% confident that the true value of the slope for this model falls within the interval [7,532.3, 10,467.7].
It implies that the price of the car increases by $7,532.3 to $10,467.7 for each mile driven by the car. In conclusion, a 95% confidence interval has been calculated for the regression line's slope, which indicates that the actual slope of the model lies between the range [7,532.3, 10,467.7].
To know more about Confidence interval visit
https://brainly.com/question/31736191
#SPJ11
6. Find QR, if area and altitude PS of ∆PQR are given
ar(∆PQR) = 180 cm2, PS = 15
Answers
Given:
Area and altitude PS of ∆PQR are ar(∆PQR) = 180cm² and PS = 15.
To find:
The measure of side QR.
Solution:
According to the given information, PS is an altitude of ∆PQR. It means QR is the base of ∆PQR.
We know that, the area of a triangle is
\(Area=\dfrac{1}{2}\times Base\times Height\)
\(ar(\Delta PQR)=\dfrac{1}{2}\times QR\times PS\)
Substituting the given values, we get
\(180=\dfrac{1}{2}\times QR\times 15\)
\(180\times 2=QR\times 15\)
\(360=QR\times 15\)
Divide both sides by 15.
\(\dfrac{360}{15}=QR\)
\(24=QR\)
Therefore, the measure of side QR is 24 cm.
what is s for the following function

Answers
11=3s+2
-2. -2
9=3s
9/3
=3
Answer:
S = 3
S = 5
S = 7
S = 9
Step-by-step explanation:
t = 3s + 2
when t = 11
11 = 3s + 2
11 – 2 = 3s
9 = 3s
s = 3
t = 3s + 2
when t = 17
17 = 3s + 2
17 – 2 = 3s
15 = 3s
s = 5
t = 3s + 2
when t = 23
23 = 3s + 2
23 – 2 = 3s
21 = 3s
s = 7
t = 3s + 2
when t = 29
29 = 3s + 2
29 – 2 = 3s
27 = 3s
s = 9
I HOPE ALL THIS HELPS
RATE AS BRAINLIEST PLS
Point M divides the line segment XY such that XM/MY=2/3 what is the location point of M
(-16/5,19/5)
(4/5,16/5)
(16/5,19/5)
(-4/5,16/5)
Answers
As per the line segment, the location point of M is option (c) (16/5,19/5)
To answer the question, it is important to understand what a line segment is. A line segment is a part of a line that connects two points, usually denoted by X and Y.
Here we have consider that in this case, the line segment XY is divided by Point M such that XM/MY is equal to 2/3.
As we all know that this means that the ratio between the two parts of the line segment is 2:3. Therefore, the location point of M is (-16/5,19/5).
Therefore, the correct option is (c).
To know more about line segment here
https://brainly.com/question/30072605
#SPJ4
Solve the system The matrix X₁ = -4; ₁ has the following eigenvalues and eigenvectors 3 (³₁); -6 -6 - (₂₂0) 2 2 = A = Correct answer X₂ = 0; V2 = Find the solution to the constant coefficient linear system d -6 £ () = (₂-2) (*) (0)) = (-4) dt (¹). PLease denote the exponential function by exp(t) rather than e**t or e^t. x(t) = 0 y(t) = 0
Answers
The solution to the given system is:
x(t) = (-2c₂/9) * exp(3t) * [3; -6] + c₂ * exp(-6t) * [-6; 2]
y(t) = (-2c₂/9) * exp(3t) * [3; -6] + c₂ * exp(-6t) * [-6; 2]
What is the system of equations?
A system of equations is a collection of one or more equations that are considered together. The system can consist of linear or nonlinear equations and may have one or more variables. The solution to a system of equations is the set of values that satisfy all of the equations in the system simultaneously.
To find the solution to the constant coefficient linear system, we can use the eigenvectors and eigenvalues provided.
Given:
X₁ = -4, eigenvalue λ₁ = 3, eigenvector v₁ = [3; -6]
X₂ = 0, eigenvalue λ₂ = -6, eigenvector v₂ = [-6; 2]
The general solution of the system is given by:
x(t) = c₁ * exp(λ₁ * t) * v₁ + c₂ * exp(λ₂ * t) * v₂
y(t) = c₁ * exp(λ₁ * t) * v₁ + c₂ * exp(λ₂ * t) * v₂
Plugging in the values:
x(t) = c₁ * exp(3t) * [3; -6] + c₂ * exp(-6t) * [-6; 2]
y(t) = c₁ * exp(3t) * [3; -6] + c₂ * exp(-6t) * [-6; 2]
To find the particular solution, we need to determine the values of c₁ and c₂ using the initial conditions:
x(0) = 0, y(0) = 0
Substituting t = 0:
x(0) = c₁ * exp(0) * [3; -6] + c₂ * exp(0) * [-6; 2] = c₁ * [3; -6] + c₂ * [-6; 2] = [0; 0]
y(0) = c₁ * exp(0) * [3; -6] + c₂ * exp(0) * [-6; 2] = c₁ * [3; -6] + c₂ * [-6; 2] = [0; 0]
This gives us the following system of equations:
3c₁ - 6c₂ = 0
-6c₁ + 2c₂ = 0
Solving this system of equations, we can find the values of c₁ and c₂. Adding twice the second equation to the first equation:
3c₁ - 6c₂ + 2(-6c₁ + 2c₂) = 0
3c₁ - 6c₂ - 12c₁ + 4c₂ = 0
-9c₁ - 2c₂ = 0
Simplifying:
9c₁ + 2c₂ = 0
We can solve this equation to find the values of c₁ and c₂:
c₁ = -2c₂/9
Therefore, the solution to the given system is:
x(t) = (-2c₂/9) * exp(3t) * [3; -6] + c₂ * exp(-6t) * [-6; 2]
y(t) = (-2c₂/9) * exp(3t) * [3; -6] + c₂ * exp(-6t) * [-6; 2]
To learn more about the system of equations visit:
brainly.com/question/25976025
#SPJ4
What are the zeros of the polynomial function? f(x)=x^3+x^2−9x−9
Answers
Answer:
1: x = -1
2: x = 3
3: x = -3
Step-by-step explanation:
f(x)=x^3+x^2−9x−9
f(x)=x^2(x+1) −9x−9
f(x) = x^2(x+1) - 9(x+1)
f(x)= (x+1)(x^2-9)
f(x) =(x+1)(x-3)(x+3)
Answer:
\(\boxed{x=-1, \ x=-3, \ x=3}\)
Step-by-step explanation:
The zeros of a function are the values of x when f(x) = 0.
\(x^3 +x^2-9x-9=0\)
Factor left side of the equation.
\(x^2(x +1)-9(x+1)=0\)
Take (x+1) common.
\((x^2-9)(x+1)=0\)
Set factors equal to 0.
First possibility:
\(x^2 -9=0\)
\(x^2 =9\)
\(x=\± \sqrt{9}\)
\(x=\± 3\)
\(x=-3 \ \mathrm{or} \ x=3\)
Second possibility:
\(x+1=0\)
\(x=-1\)
hey can you guys please confirm my answer, i got B

Answers
have a great day :))
194 people must be split into 2 equal groups. how many people in eachgroup
fast if possible
Answers
So there is 97 people in each group
I really need help with part a and b, please help. Incorrect answers will be downvoted, correct answers will be upvoted. 1. The army is interested in characterizing the acoustic signature of a helicopter. The following data show measurements of acoustic pressure (made dimensionless) for a two-bladed helicopter rotor through of a rotor revolution. The data points are equally spaced in time, and the period of the data collection is of a second. p=00.00040.0015 0.0028 0.0040 0.0048 0.0057 0.0071 0.0095 0.0134 0.0185 0.02420.0302 0.0364 0.0447 0.0577 0.0776 0.0955 0.0907 -0.0477 -0.0812 -0.0563 -0.0329 -0.0127 0.0032 0.0147 0.0221 0.0256 0.0255 0.0222 0.0170 0.0112 0.0064 0.0035 0.0023 0.0020 0.0019 0.0016 0.0009 0.0002 a) Find the real discrete Fourier transform for this data set. (b) Any term in the Fourier series can be written: ak Cos(kwt)+bk sin(kwt) =ck Cos(kwt+$k) ak Find the ck's and plot their amplitude on a bar graph vs. k to illustrate the relative size of each term in the series. Explain the significance of the plot
Answers
(a) The real discrete Fourier transform (DFT) is calculated for the given data set to analyze the helicopter's acoustic signature.
(b) To obtain the ck values and illustrate the relative size of each term in the Fourier series, we calculate the magnitude of each coefficient and plot their amplitudes on a bar graph against the corresponding frequency component, k.
To analyze the helicopter's acoustic signature, the real DFT is computed for the provided data set. The DFT transforms the time-domain measurements of acoustic pressure into the frequency domain, revealing the different frequencies present and their corresponding amplitudes. This analysis helps in understanding the spectral characteristics of the helicopter's acoustic signature and identifying prominent frequency components.
Using the Fourier series representation, the amplitudes (ck's) of the different frequency components in the Fourier series are determined. These amplitudes represent the relative sizes of each term in the series, indicating the contribution of each frequency component to the overall acoustic signature. By plotting the amplitudes on a bar graph, the relative strengths of different frequency components become visually apparent, enabling a clear comparison of their importance in characterizing the helicopter's acoustic signature.
Learn more about Fourier transform
brainly.com/question/29063535
#SPJ11
Find the value of r so the line that passes through the pair of points has the given slope. ( − 2 , 8 ) , ( r , 4 ) , m = − 1 2
Answers
The line that passes through the pair of points has the given slope. ( − 2 , 8 ) , ( r , 4 ) , m = − 1 2, then the intersection with the domain is r = -5/3.
The line that passes through the pair of points has the given slope is,
( − 2 , 8 ) , ( r , 4 ) and m = -12
What is Slope :Slope, numerical measure of a line's inclination relative to the horizontal. In analytic geometry, the slope of any line, ray, or line segment is the ratio of the vertical to the horizontal distance between any two points on it (“slope equals rise over run”).
m = rise/run
\(m=\frac{y_{2} -y_{1} }{x_{2}-x_{1} }\)
Where,
m = slope
\((x_{1} ,y_{1} )\) = coordinates of first point in the line
\((x_{2} ,y_{2} )\) = coordinates of second point in the line
Then, we can find the \(m_{1}\)
We can use these two values, ( − 2 , 8 ) , ( r , 4 )
x1 = -2
y1 = 8
x2 = r
y2 = 4
m = \(\frac{4-8}{r-(-2)}\)
\(m = \frac{-4}{r+2}\)
We can substitute m= -12 value into m= -(4/r+2)
So,
We can write,
-12 = \(\frac{-4}{r+2}\)
We can find the domain,
If the fraction is defined, the dominator can not be equal to zero.
2 + r ≠ 0
Rearrange variables to the left side of the inequality,
r ≠ -2
Append the inequality as the domain,
r ≠ -2
We can solve the equation,
-12 = \(\frac{-4}{r+2}\)
Multiply both sides of equation by the common denominator,
-12 (r+2) = -4(r+2)/ (r+2)
Reduce the fractions,
-12 (r+2) = -4
Apply the distributive property,
-12r - 24 = -4
Rearrange variable to the left side of the equation,
-12r = -4 + 24
Calculate the sum or difference,
-12r = 20
Divide both sides of the equation by the coefficient of variables,
r = - 20/12
r = -5/3
Therefore,
The intersection with the domain is r = -5/3, so the line that passes through the pair of points has the given slope. ( − 2 , 8 ) , ( r , 4 ) , m = − 12.
To learn more about information visit Slope :
brainly.com/question/208768
#SPJ1
this is due in 30 mins

Answers
11) The pre-image, R at the point (-2, 3) on the grid shown produces an image following the reflection across the line y = 2·x - 3 as follows;
I. The line \(\overline{RR'}\) which is obtained from the image R' following a reflection across the line y = 2·x - 3, is perpendicular to the line y = 2·x - 3, because the points R and R' are vertically opposite each other, therefore, the slope is the negative inverse of the slope of y = 2·x - 3, which is -0.5
II. Please find attached the graph made using MS Excel showing the points R and R'
What is a reflection transformation?A reflection transformation is one in which a point is reflected across a line such that the distances of the image and the pre-image from the line are the same and the line acts like a mirror producing an image of the object.
The coordinates of point R = (-2, 3)
The equation of the line of reflection is; y = 2·x - 3
The coordinates of the image of a point, (x₁, y₁) reflected across a line, a·x + b·y + c = 0, is found as follows;
The image of is found using the formula;
\(\dfrac{x - x_1}{a} =\dfrac{y-y_1}{b} = -\dfrac{2\cdot (a\cdot x_1+b\cdot y_1+c)}{a^2+b^2}\)
The equation, y = 2·x - 3, can be expressed in the form a·x + b·y + c = 0, as follows;
y = 2·x - 3
0 = 2·x - 3 - y
Therefore;
a = 2, b = -1, and c = -3
(x₁, y₁) = (-2, 3)
\(\dfrac{x - (-2)}{2} = -\dfrac{2\times (2\times (-2)- 3-3)}{2^2+(-1)^2}=4\)
\(\dfrac{x +2}{2} = 4\)
x = 2× 4 - 2 = 6
x = 6
\(\dfrac{y-3}{-1} = 4\)
y = 4 ×(-1) + 3 = -1
The coordinates of the image, (x, y) = (6, -1)
The slope of the line is -(1/2)
The equation of the perpendicular line is therefore;
(y - 3) = -0.5·(x - (-2)) = -0.5·x - 1
y = -0.5·x - 1 + 3 = -0.5·x + 2
Equation of the perpendicular line through R; y = -0.5·x + 2
The intersection point is therefore;
-0.5·x + 2 = 2·x - 3
2.5·x = 5
x = 5 ÷ 2.5 = 2
y = 2×2 - 3 = 1
y = 1
The point is therefore, (2, 1)
The difference in the x-values = 2 - 2 = 4
The difference in the y-value = 1 - 3 = -2
Therefore, 4 is added to the x-value of the point (2, 1) and 2 is subtracted to get the image as follows;
(x, y) = (2 + 4, 1 - 2) = (6, -1)
The slope of \(\overline{RR'}\) = (3 - (-1))/(-2 - 6) = -0.5
b. Graphically, the equation of the line \(\overline{RR'}\) can be used to find the point R', by adding the horizontal distance and subtracting the vertical distance of the point R from the the point of intersection of the two lines.
Please find attached the graph showing R and the image R' created with MS Excel.
Learn more about reflection transformation in geometry here;
https://brainly.com/question/4070544
#SPJ1
For the normal range of summer temperatures the number of chirps made by a cricket in a minute is predictable. For example,
at 72°F the cricket chirps 140 times a minute. At 80 Fthe cricket chirps 172 times a minute. What is the temperaturewhen the
cricket chirps 180 times a minute?
Answers
The temperature when the cricket chirps 180 times a minute = \(83.72^{\circ} F\)
Given:
The normal range of summer temperatures the number of chirps made by a cricket in a minute is predictable.
At 72°F the cricket chirps 140 times a minute. At 80° Fthe cricket chirps 172 times a minute.
i.e. frequency of chirps is directly proportional to the temperature.
Computation:
Let x be the temperature when the cricket chirps 180 times a minute, then
\(\dfrac{x}{180}=\dfrac{80}{172}\ \ \ \ \ [\text{Using direct variation equation:} \frac{x_}{y_1}=\frac{x_2}{y_2}}]\\\\\Rightarrow\ x\approx83.72^{\circ} F\)
Hence, The temperature when the cricket chirps 180 times a minute = \(83.72^{\circ} F\)
Learn more:
https://brainly.com/question/24723179
Determine the truth value of each conditional statement. If true, explain your reasoning. If false, give a counterexample.If two angles are acute, then they are supplementary.
Answers
The truth value of the given statement is false.
The given conditional statement is “If two angles are acute, then they are supplementary.” To determine the truth value of the statement, we have to consider its hypothesis and conclusion.If two angles are acute (hypothesis), then they are supplementary (conclusion).
Let’s take some acute angles and check whether they are supplementary or not. Consider two acute angles of 60° each. As the sum of the measures of two acute angles is less than 180°, they can’t be supplementary. Therefore, the statement is false, and a counterexample has been given.
Hence, the truth value of the conditional statement is false. If two angles are acute, they can't be supplementary.
Proof:Suppose we consider two acute angles A and B. If the two angles are acute, then it means their measures are less than 90°.A + B < 180° (sum of the measures of the angles)< 90° + 90°= 180°
Hence, the sum of the measures of the two acute angles is less than 180°. Therefore, the given statement is false.
The truth value of the given statement is false.
Know more about acute angles here,
https://brainly.com/question/2761036
#SPJ11
-[-/7.14 Points] DETAILS LARPCALC11 6.4.036. Find the angle (in radians) between the vectors. (Round your answer to two decimal places.) u = 4i - 6j v = 5i + 4j 0 =
4. [-/7.14 Points] DETAILS LARPCAL
Answers
The angle (in radians) between vectors u and v is approximately 1.66 radians, rounded to two decimal places.
To find the angle between two vectors, we can use the dot product formula and the magnitudes of the vectors. Let's calculate the angle between vectors u and v:
Given:
u = 4i - 6j
v = 5i + 4j
Step 1: Calculate the dot product of u and v.
The dot product of two vectors u and v is given by:
u · v = |u| |v| cosθ
where |u| and |v| are the magnitudes of vectors u and v, respectively, and θ is the angle between them.
To calculate the dot product, we multiply the corresponding components of u and v and sum them:
u · v = (4 * 5) + (-6 * 4) = 20 - 24 = -4
Step 2: Calculate the magnitudes of vectors u and v.
The magnitude of a vector is given by:
|u| = √(u₁² + u₂²)
For vector u:
|u| = √((4)² + (-6)²) = √(16 + 36) = √52 ≈ 7.21
For vector v:
|v| = √((5)² + (4)²) = √(25 + 16) = √41 ≈ 6.40
Step 3: Calculate the angle θ.
Using the dot product formula mentioned earlier, we have:
-4 = (7.21)(6.40)cosθ
Solving for cosθ:
cosθ = -4 / (7.21 * 6.40) ≈ -0.086
To find θ, we can take the inverse cosine (arccos) of cosθ:
θ ≈ arccos(-0.086) ≈ 1.66 radians
Know more about vectors here:
https://brainly.com/question/24256726
#SPJ11
everyone pls answer the questions I posted they are urgent
Answers
Answer:
unfortunately there's no questions to be answered
Which term refers to a process that is deployed to ensure the confidentiality and integrity of data while being stored or when it is transmitted Brainly?
Answers
The term refers to a process that is deployed to ensure the confidentiality and integrity of data while being stored or when it is transmitted is called "Encryption".
What is encryption?Data encryption is a computational procedure that converts plaintext/cleartext (unencrypted, readable data) in ciphertext (encrypted data), which is only available to authorised users with the correct cryptographic key.
Some key features regarding the encryption are-
Data is converted into cipher text through encryption that used a cipher (an encrypted technique) and an encryption key. A key (the same key for symmetric key encryption; a distinct, related value for asymmetric cryptography) is employed to decode the cipher - text into the original value once it has been communicated to the receiving party. Since encryption keys function similarly to physical keys, only users who have the appropriate key can "unlock" or decode the encrypted information.Encryption is frequently important to uphold compliance laws imposed by numerous organisations or standards bodies, in addition to the strong data privacy protection it offers.To know more about encryption, here
https://brainly.com/question/4280766
#SPJ4
thankssss plzzz helpp

Answers
Say, for example, the correlation is 0.75 between fat content (measured in grams) and cholesterol level (measured in milligrams) for 20 different brands of American cheese slices. If cholesterol level were changed to being measured in grams (where 1 gram = 1000 milligrams), what effect would this have on the correlation?
Answers
If cholesterol level were changed to being measured in grams instead of milligrams, the correlation between fat content and cholesterol level would not be affected.
This is because correlation is a measure of the strength and direction of the linear relationship between two variables, and converting the units of measurement does not change the underlying relationship between the variables. So, the correlation coefficient of 0.75 would remain the same whether cholesterol level is measured in milligrams or grams.
The correlation between fat content and cholesterol level for the 20 different brands of American cheese slices is 0.75. If you change the measurement of cholesterol level from milligrams to grams (1 gram = 1000 milligrams), it will not affect the correlation. The correlation coefficient will remain 0.75, as it is unit-less and only represents the strength and direction of the relationship between the two variables.
Visit here to learn more about correlation coefficient : https://brainly.com/question/27226153
#SPJ11
A random sample of 64 sat scores of students applying for merit scholarships showed an average of 1400 with a standard deviation of 240. the 95onfidence interval for the population mean sat score is: ________
a. 1.96. b. 1.998.
c. 1.645. d. 1.28.
Answers
The 95% confidence interval for the population mean SAT score is given as follows:
(1340, 1460).
How to calculate the confidence interval?The confidence interval is calculated using the t-distribution, as the standard deviation for the population is not known, only for the sample.
The bounds are obtained according to the equation defined as follows:
\(\overline{x} \pm t\frac{s}{\sqrt{n}}\)
In which the variables of the equation are presented as follows:
\(\overline{x}\) is the sample mean.t is the critical value.n is the sample size.s is the standard deviation for the sample.In the context of this problem, the values of these parameters are given as follows:
\(\overline{x} = 1400, n = 64, s = 240\)
The critical value, using a t-distribution calculator, for a two-tailed 95% confidence interval, with 64 - 1 = 63 df, is t = 1.998.
Then the lower bound of the interval is of:
1400 - 1.998 x 240/sqrt(64) = 1340.
The upper bound of the interval is of:
1400 + 1.998 x 240/sqrt(64) = 1460.
More can be learned about the t-distribution at https://brainly.com/question/17073112
#SPJ1
please help asappp :)

Answers
Answer:
A = 22a
B = 5
C = 3x
D = 2y
Step-by-step explanation:
\(\frac{22ay+9x^{2}y^{3}-5x^{3}}{12\left(xy\right)^{2}} \\ \)
Find a linear function that passes through the points (4, 5) and (6, 13)
Answers
The linear function that passes through the points (4, 5) and (6, 13) is y = 4x - 11.
To find a linear function that passes through the points (4, 5) and (6, 13), we can use the slope-intercept form of a linear equation, which is y = mx + b, where m represents the slope of the line and b represents the y-intercept.
First, we need to calculate the slope (m) using the formula:
m = (y₂ - y₁) / (x₂ - x₁)
Let's substitute the values from the given points:
m = (13 - 5) / (6 - 4)
m = 8 / 2
m = 4
Now that we have the slope, we can proceed to find the y-intercept (b). We can choose either of the two given points and substitute the coordinates into the equation:
Using point (4, 5):
5 = 4(4) + b
5 = 16 + b
b = -11
Therefore, the linear function that passes through the points (4, 5) and (6, 13) is y = 4x - 11.
To know more about linear functions, refer here:
https://brainly.com/question/21107621#
#SPJ11
3x^2-20x-7=0 con you solve this
Answers
Answer:
x = 7 and x = -1/3
Step-by-step explanation:
To solve the quadratic equation 3x^2 - 20x - 7 = 0, we can use the quadratic formula:
x = (-b ± sqrt(b^2 - 4ac)) / 2a
where a, b, and c are the coefficients of the quadratic equation.
In this case, a = 3, b = -20, and c = -7. Substituting into the quadratic formula, we get:
x = (-(-20) ± sqrt((-20)^2 - 4(3)(-7))) / 2(3)
Simplifying the expression inside the square root:
x = (20 ± sqrt(400 + 84)) / 6
x = (20 ± sqrt(484)) / 6
x = (20 ± 22) / 6
So, we have two solutions:
x = (20 + 22) / 6 = 7
x = (20 - 22) / 6 = -1/3
Therefore, the solutions to the quadratic equation 3x^2 - 20x - 7 = 0 are x = 7 and x = -1/3.
Given points A(-1,4) and B(x,7), determine the value(s) of x if AB=5cm
Answers
The value of x is either 3 or -5 based on the distance formula.
What is a co-ordinate system?
In pure mathematics, a coordinate system could be a system that uses one or additional numbers, or coordinates, to uniquely confirm the position of the points or different geometric components on a manifold like euclidean space.
Main body:
according to question
Given points A(-1,4) and B(x,7)
Also AB = 5 cm
Formula of distance = \(\sqrt{(y1-y2)^{2}+(x1 -x2)^{2} }\)
here by using points ,
5 = \(\sqrt{(x+1)^{2} +(7-4)^{2} }\)
taking square on both side ,'
25 = \((x+1)^{2} +3^{2}\)
25-9 = (x+1)²
16 = (x+1)²
taking square root on both sides,
x+1= ±4
x = 4-1 = 3 or x = -4-1 = -5
Hence value of x is either 3 or -5.
To know more about point , visit:
https://brainly.com/question/26310043
#SPJ1
The number of hours of sunshine in Barbados for successive days during a and 11.8. Find the daily certain week were 11.1, 11.9, 11.2, 12.0, 11.7, 12.9 average. The following week the daily average was 11 hours. How many more hours of sunshine were there the first week than the second?
Answers
Answer:
5.6
Step-by-step explanation:
11*7=77
11.8*7= 82.6
82.6-77=5.6
Use the drawing tool(s) to form the correct answer on the provided number line. Will brought a 144-ounce cooler filled with water to soccer practice. He used 16 ounces from the cooler to fill his water bottle. He then took out 16 plastic cups for his teammates and put the same amount of water in each cup. Find and graph the number of ounces of water, x, that Will could have put in each cup.

Answers
According to the information, we can infer that the number of ounces of water, x, that Will could have put in each cup is 8 ounces.
What is the number of ounces of water "x" that Will could have put in each cup?Will initially had a cooler filled with 144 ounces of water. After using 16 ounces to fill his water bottle, there were 144 - 16 = 128 ounces of water remaining in the cooler.
Will then took out 16 plastic cups for his teammates. Since the same amount of water was put in each cup, the remaining amount of water, 128 ounces, needs to be divided equally among the cups.
Dividing 128 ounces by 16 cups gives us 8 ounces of water for each cup.
So, Will could have put 8 ounces of water in each cup.
Learn more about water in: https://brainly.com/question/28465561
#SPJ1

solve please (image attached)

Answers
Answer:
x = 1/a
Step-by-step explanation:
To solve 7ax + 8ax = 9ax + 6 for x, we can start by combining like terms on both sides of the equation:
7ax + 8ax = 9ax + 6
becomes
15ax = 9ax + 6
Next, we can subtract 9ax from both sides of the equation:
15ax - 9ax = 9ax + 6 - 9ax
becomes
6ax = 6
Finally, we can divide both sides of the equation by 6a to find the value of x:
6ax / 6a = 6 / 6a
becomes
x = 1/a
So, the solution for x is x = 1/a.