165% as a fraction. PLEASE I NEED IT NOW
Answers
Answer:
33/20
Step-by-step explanation:
Answer:
1.65 is the answer just put a decimal
Related Questions
The number of different positive two-digit whole number isa) 90b) 91c) 99d) 89
Answers
The whole numbers from 10 to 99 are positive and have two digits, we can find the amount of them like this:
from 10 to 19->10 numbers
from 20 to 29->10 numbers
from 30 to 39->10 numbers
from 40 to 49->10 numbers
from 50 to 59->10 numbers
from 60 to 69->10 numbers
from 70 to 79->10 numbers
from 80 to 89->10 numbers
from 90 to 99->10 numbers
Since we have 9 groups of 10 numbers, if we add them we get 90.
Then, the number of different positive two-digit whole number is 90
What is the value of v?

Answers
Answer:
34 degrees
Step-by-step explanation:
If you know the 2 interior angles of a triangle, you can find the 3rd.
This is useless since this is a right triangle.
In this case:
v + 46 = 90
v = 34 degrees
You are welcome!
Kayden Kohl
8th Grade Student
Solve (2 - x)^2 < 4/25
Answers
Answer:
8/5 < x< 12/5
Step-by-step explanation:
(2 - x)^2 < 4/25
Take the square root of each side
sqrt((2 - x)^2) <±sqrt( 4/25)
Make two equations
2-x < 2/5 2-x > -2/5
Subtract 2 from each side
2-x-2 < 2/5 -2 2-x-2 > -2/5-2
-x < 2/5 - 10/5 -x > -2/5 - 10/5
-x < -8/5 -x > -12/5
Multiply by -1, remembering to flip the inequality
x> 8/5 x < 12/5
8/5 < x< 12/5
9t+5=7-2t SLOVE THE EQUATION AND CHECK THE SOULTION
Answers
Answer:
t=1/6 or 0.166
Step-by-step explanation:
add like terms: 12t=2
divide by 12: t=1/6
simply to decimal: 0.166
Answer:
ok so id.k how to show you step by step how to get the solution but i can give you the answer so
t=2/11
or in decimal form
t=0.18
Step-by-step explanation:
The radius of a circle is 13ft. Find it’s area in terms of pi.
Answers
Answer:
\(A = 169\pi \text{ ft}^2\)
Step-by-step explanation:
We can find the area of the circle using the formula:
\(A=\pi r^2\)
↓ plugging in the given radius value
\(A=\pi (13\text{ ft})^2\)
\(\boxed{A = 169\pi \text{ ft}^2}\)
we are being taught to do (eg. x+ (x+2) + (x+4) ) but I dont know how to get the numbers 72,74, and 76
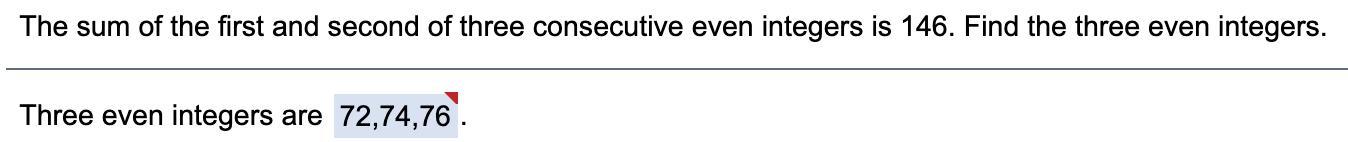
Answers
You can write three consecutive even numbers as follow:
2x, 2(x + 1), 2(x + 2)
Considert that the sum of the first number and the second one is 146, then, you have:
2x + 2(x + 1) = 146
Solve the previous equation for x, as follow:
2x + 2x + 2 = 146 simplify like terms left side
4x + 2 = 146 subtract 2 both sides
4x = 146 - 2
4x = 144 divide by 4 both sides
x = 144/4
x = 36
Next, replace the previous value of x into the expressions for the even numbers:
2x = 2(36) = 72
2(x + 1) = 2(36 + 1) = 74
2(x + 2) = 2(36 + 2) = 76
Hence, the even numbers are 72, 74 and 76
.A bicycle normally sells for $475. The bicycle was discounted 30% for a
sale. After the sale was over, the new price of the bicycle was 25%
higher than the sale price. What was the new price of the bicycle?
Answers
Answer:
415.63
Step-by-step explanation:
Multiply the price by the sales tax to find out how much money the sales tax will add.
Answer:
$415.63
Step-by-step explanation:
475
after 30%
475 times .30 = 142 5
475 - 142.5 = 332.5 <- sale price
332.5 times .25 = 83.125
332.5 + 83.125 = 415.625 <- new price
i need help please and thanks

Answers
Answer:
Step-by-step explanation:
There are an infinite amount of possibilities with the solution of (4,1). As proof, plot the point (4,1) on a coordinate system. Then, draw straight lines that pass through that point. These lines can differ in slopes. They can be either be positive, negative, vertical, or horizontal.
x = 4
y = 1
x + y = 5
name me brainleist and say thank you, and rate 5 stars.
Identify the angles that are coterminal with 135 degrees choose all that apply

Answers
Answer:ok
Step-by-step explanation:
1.The base length of a rectangle is multiplied by 8. How does this affect the area?
A. area is 2x bigger
B. area is 4x bigger
C. area is 8x bigger
D. area is 16x bigger
2.The base length and the width length of a rectangle are both multiplied by 4. How does this
affect the area?
A. area is 2x bigger
B. area is 4x bigger
C. area is 8x bigger
D. area is 16x bigger
3.The radius of a circle is tripled. How does this affect the area?
A. area is 3x bigger
B. area is 6x bigger
C. area is 9x bigger
D. area is 18x bigger
Answers
Answer:
1. C - 8x bigger
2. D - 16x bigger
3. A - 3x bigger
Step-by-step explanation:
Answer:
1. C
2. D
3. A
Step-by-step explanation:
What is 2/5m=17/4 please help me bc I’m confused
Answers
Step-by-step explanation:
To find m, we need to divide 2/5 from both sides of the equation given.
Divide:
\(\frac{2/5}{2/5} x=\frac{17/4}{2/5}\)
Solving Dividing:
2/5 cancels out.
\(\frac{17}{4} \div \frac{2}{5} =\frac{17}{4} \times\frac{5}{2} =85/8\)
Equation:
\(x=\frac{85}{8}\)
\(x =10.625, or: 10\frac{5}{8}\)
429 is 4 hundreds 29
Answers
Answer: yes
Step-by-step explanation: because that how many times it could go in too it
Answer:
huh?
Step-by-step explanation:
if your asking if 429 is 4 hundred and 29, then yes
Sketch and label a graph of both an increasing and a decreasing exponential function.
Answers
An exponential function is one in which the independent variable x appears in the exponent and has a constant a as its base. Its expression is:
\(f(x)=a^x\)With a being a positive real, a > 0, and different from 1, a ≠ 1.
When 0 < a < 1, then the exponential function is a decreasing function and when a > 1, it is an increasing function.
For example: the function
\(f(x)=2^x\)Since a = 2 > 1, the function is increasing. We have the graph below:
And the function
\(f(x)=0.5^x\)Since a = 0.5 < 1, the function is decreasing. Then, the graph is:
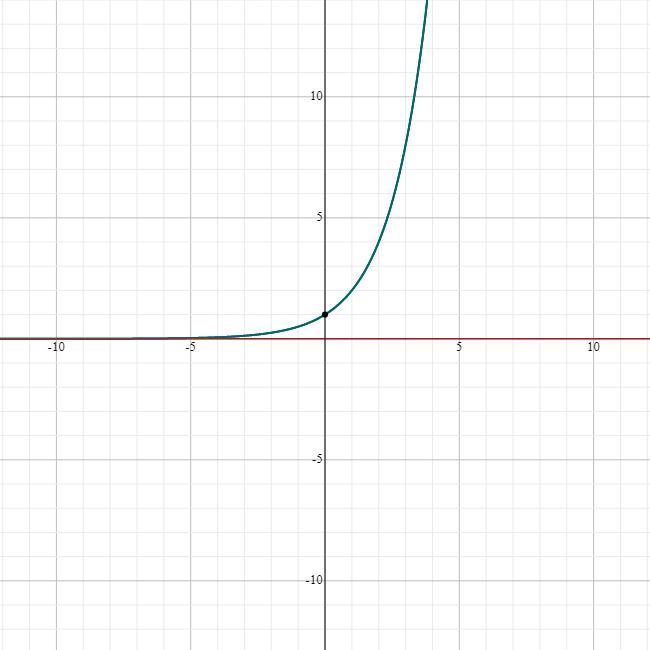

For each pair of functions f, g below, find f(g(x)) and g(f(x))
Then, determine whether and are inverses of each other.
Simplify your answers as much as possible.
(Assume that your expressions are defined for all in the domain of the composition.
You do not have to indicate the domain.)

Answers
Answer:
See below
Step-by-step explanation:
Part A
\(f(g(x))=f(\frac{x}{3})=3(\frac{x}{3})=x\\g(f(x))=g(3x)=\frac{3x}{3}=x\)
Since BOTH \(f(g(x))=x\) and \(g(f(x))=x\), then \(f\) and \(g\) are inverses of each other
Part B
\(f(g(x))=f(\frac{x+1}{2})=2(\frac{x+1}{2})+1=x+1+1=x+2\\g(f(x))=g(2x+1)=\frac{(2x+1)+1}{2}=\frac{2x+2}{2}=x+1\)
Since BOTH \(f(g(x))\neq x\) and \(g(f(x))\neq x\), then \(f\) and \(g\) are NOT inverses of each other
25/100 simplified ? and if there’s any work pls show it
Answers
Answer:
\( \frac{1}{4} \)
Step-by-step explanation:
25/100
divide both sides with 25
\( \frac{25 \div 25 }{100 \div 25} \)
simplify
= 1/4
Answer:
1/4
Step-by-step explanation:
Find HCD (Highest Common Factor) for both numerator and denominator.
The HCF for 25 and 100 is 25
Now divide the numerator and denominator by 25
(25/25) / (100/25)
1/4
And Viola, you got your simplified form!
Henry correctly factored 42? + 52 - 6 as (4% - 3)(₴ + 2)
• He then claimed that the zeros of that quadratic function are located at
*=-=
and r = 2 . Did Henry correctly find the zeros of the function?
O Yes, Henry correctly found the zeros of the function.
O No, the zeros of the function are at x = 4 and =-2
• No, the zeros of the function are at z = - 5 andx = 2.
• No, the zeros of the function are at & = 4 and ≥ = -2
I attached the question and answer choices
Please help

Answers
Answer:
No, the zeros of the function are at x = 3/4 and x = –2
Step-by-step explanation:
the equation
4x² + 5x – 6 = 0
(note: since there is a coefficient of x² we need to multiply it to the last term(6))
4x² + 5x – 24 = 0
the factors are :- 8x and – 3x
4x² + 8x – 3x – 6 = 0
4x( x + 2) –3( x + 2) = 0
( 4x – 3)( x + 2) = 0
the zeros will be
4x – 3 = 0
4x = 3
\(x = \frac{3}{4} \)
x + 2 = 0
x = – 2
the zeros are x= 3/4 or –2
i hope this helps
What is the point-slope form of a line that has a slope of 5 and passes through the point (3,-4)? y-3=5[x-(-4)] -4-y₁ = 5(3-x₁) y-(-4)=3(x - 5) y-(-4)= 5(x-3)
Answers
Answer:
y -(-4)= 5(x -3)
Step-by-step explanation:
The point-slope form of a line is given by y -y₁= m(x -x₁), where m is the slope.
Given
Slope, m= 5
(x₁, y₁)= (3, -4)
Substitute the given information into the equation:
y -(-4)= 5(x -3)
The 4th option is thus correct.
_____
Simplifying the equation:
y +4= 5(x -3)
Additional:
For a similar question on point-slope form, do check out the following!
https://brainly.com/question/837699A line intersects the point (-11, 4) and has
a slope of -2. What are the inputs to the
point-slope formula?
y - [?] = [ ](x-[])
Answers
Answer: Point slope form is y-y1=m(x-x1)
Step-by-step explanation:
Here y1=4
x1=-11
m i.e slope=-2
And there you go.
6x + 9 = -12. What is the value of x?
(Six x plus nine, equals negative twelve)
Answers
Answer:
The answer is x=-7/2
Step-by-step explanation:
hope this helps
6x + 9 = -12
6x+9-9=-12-9
6x=-21
To find the x divide both side by 6.
6x/6=-21/6
x= -7/2
the answer to this question is = (- 7/2)
Write a program that reads a list of integers into a list as long as the integers are greater than zero, then outputs the smallest and largest integers in the list.
Ex: If the input is:
10
5
3
21
2
-6 (negative six, the format is weird on stackoverflow)
the output is:
2
21
You can assume that the list of integers will have at least 2 values.
Answers
Python program that reads a list of integers into a list and outputs the smallest and largest integers in the list by using loops.
numbers = []
while True:
num = int(input())
if num > 0:
numbers.append(num)
else:
break
min_num = numbers[0]
max_num = numbers[0]
for num in numbers:
if num < min_num:
min_num = num
if num > max_num:
max_num = num
print(min_num)
print(max_num)
In this program, we use the same while loop as before to read integers from the user and add them to the numbers list. After the loop completes, we initialize two variables called min_num and max_num to the first value in the numbers list.
We then use a for loop to iterate over each value in the numbers list. For each value, we compare it to the current values of min_num and max_num. If the value is less than min_num, we update min_num to be the new minimum value. If the value is greater than max_num, we update max_num to be the new maximum value.
After the loop completes, we print the final values of min_num and max_num to the console.
Read more about Programming:
https://brainly.com/question/14841987
#SPJ4
The Fahrenheit temperature readings on 66 Spring mornings in New York City are
summarized in the table below. Construct and label a frequency histogram of the data
with an appropriate scale.
Temp (°F) Number of Days.
30-39
2
40-49
26
50-59
28
60-69
8
70-79
2
Graph answer Click and drag to make a rectangle. Click a rectangle to delete it.
Answers
To construct a frequency histogram based on the given temperature data, we will use the temperature ranges as the x-axis and the number of days as the y-axis.
The temperature ranges and their corresponding frequencies are as follows:
30-39: 2 days
40-49: 26 days
50-59: 28 days
60-69: 8 days
70-79: 2 days
To create the histogram, we will represent each temperature range as a bar and the height of each bar will correspond to the frequency of days.
Using an appropriate scale, we can label the x-axis with the temperature ranges (30-39, 40-49, 50-59, 60-69, 70-79) and the y-axis with the frequency values.
Now, we can draw rectangles (bars) on the graph, with the base of each rectangle corresponding to the temperature range and the height representing the frequency of days. The height of each bar will be determined by the corresponding frequency value.
For such more question on frequency
https://brainly.com/question/254161
#SPJ8
Simple interest to find the ending balance $460 at 13% for
2
years
Answers
Answer:
$568.16
Step-by-step explanation:
First, converting R percent to r a decimal
r = R/100 = 13%/100 = 0.13 per year,
then, solving our equation
I = 416 × 0.13 × 2 = 108.16
I = $ 108.16
The simple interest accumulated
on a principal of $ 416.00
at a rate of 13% per year
for 2 years is $ 108.16.
The table shows the distance, in feet, a ball travels t seconds after being dropped from a 980-foot building. The equation d(t) = 9.8t2 models the function shown in the table. What are the restricted domain and range of the function? D = {0, 2, 4, 6, 8} and R = {0, 39.2, 156.8, 352.8, 627.2} D = {0 ≤ t ≤ 8} and R = {0 ≤ d(t) ≤ 627.2} D = {0 ≤ t ≤ 8} and R = {0 ≤ d(t) ≤ 980} D = {0 ≤ t ≤ 10} and R = {0 ≤ d(t) ≤ 980}
Answers
Answer:
D
Step-by-step explanation:
Answer:
D
Step-by-step explanation:
On edge
13. Determine if the following statement is true or false. Explain your reasoning.
The graph of a non-vertical straight line is always a function, but the graph
of a function is not always a straight line.
Answers
The evaluation of the statements with regards to the graph of a function are;
The graph of non-vertical straight line is always a function, but the graph of a function is not always a straight line is true.What is a function?A function maps an input value to an output based on a definition or rule.
First part of the statement;
The graph of a non-vertical straight line has a range of values for the slope, m, of 0 ≤ m < ∞
The equation of a straight line function is of the form; y = m·x + c
Therefore;
The graph of a non-vertical straight line can be represented by the equation, y = m·x + c, where y has possible values of; -∞ < y < ∞, which indicates that as x increases or decreases, y increases (or decreases), such that each value of x maps unto only one value of y, which indicates that the graph is a function. The statement is therefore true.
Second part of the statement.
The graph of the quadratic function; y = a·x² + b·x + c has a shape of a parabola, therefore, the statement, the graph of a function is not always a straight line is true also.
Learn more about functions here: https://brainly.com/question/10687170
#SPJ1
The area of a rectangle is 3x2 - 12x square yards. If the width is 3x yards, what is the length of the rectangle?
Answers
Answer:
x - 4 yards.
Step-by-step explanation:
Given:
Area of rectangle = 3x^2 - 12x square yards
Width = 3x yards
To find:
Length of rectangle
Solution:
The area of a rectangle is equal to the product of its length and width.
Area of rectangle = Length * Width
Substituting the given values, we get:
3x^2 - 12x = Length * 3x
Length =( 3x^2 - 12x )3x
Length = x-4
Therefore, the length of the rectangle is x - 4 yards.
Answer: The length of the rectangle is x - 4 yards.
Step-by-step explanation:
We can create an equation to solve this word problem, where the variable L = length.
3x × L = \(3x^2 - 12x\)
We need to solve for the variable L, to find the length of the rectangle.
First lets factor the right side of the equation to make it easier to divide with.
3x × L = \(3x^2 - 12x\)
We can factor out 3x from the right side of the equation.
3x × L = 3x(x - 4)
Now we need to get the variable L by itself (isolating the variable). In order to do that, we can divide both sides by 3x.
3x × L = 3x(x - 4)
/3x /3x
L = x - 4
The length of the rectangle is x - 4 yards.

Two cars are traveling towards a hotel on the same road. From the edge of the hotel, 600 feet high, Spiderman sits on the rooftop thinking about the depression angle needed to reach each car. If the depression angle to the nearest car is 52 degrees, and the depression angle to the farther car is 46 degrees, how far apart must the two cars be from each other?
Make a sketch, solve the problem, and round your answer to the nearest hundredth of a foot.
Answers
The two cars must be approximately 177.34 feet apart from each other for Spiderman to have different depression angles to each car.
To find the distance between the two cars, we can use trigonometry and the concept of similar triangles. Let's denote the distance between Spiderman and the nearest car as d1 and the distance between Spiderman and the farther car as d2.
In a right triangle formed by Spiderman, the height of the hotel, and the line of sight to the nearest car, the tangent of the depression angle (52 degrees) can be used:
tan(52) = 600 / d1
Rearranging the equation to solve for d1:
d1 = 600 / tan(52)
Similarly, in the right triangle formed by Spiderman, the height of the hotel, and the line of sight to the farther car, the tangent of the depression angle (46 degrees) can be used:
tan(46) = 600 / d2
Rearranging the equation to solve for d2:
d2 = 600 / tan(46)
Using a calculator, we can compute:
d1 ≈ 504.61 feet
d2 ≈ 681.95 feet
The distance between the two cars is the difference between d2 and d1:
Distance = d2 - d1
Plugging in the values, we have:
Distance ≈ 681.95 - 504.61
Distance ≈ 177.34 feet
For more such question on angles. visit :
https://brainly.com/question/25770607
#SPJ8
A manager drew this box-and-whisker plot to represent the number of minutes each of his 27 employees took on their break. Each employee took a different amount of time.
How many employees took a break longer than 49 minutes?
Help please!
Note: Put the correct answer! I don't want to get this wrong!
Thank you <3
Answers
Approximately 7 employees took a break longer than 49 minutes.
We have,
In a box-and-whisker plot, the box represents the interquartile range (IQR), which includes the middle 50% of the data.
The line within the box represents the median.
The "whiskers" extend to the minimum and maximum values, excluding any outliers.
Given the information provided:
Median = 41
Q1 = 37
Q3 = 49
Largest = 55
Smallest = 35
Since Q3 represents the upper quartile and corresponds to the boundary for the upper 25% of the data, we can conclude that 25% of the employees took a break longer than 49 minutes.
Now,
The number of employees who took a break longer than 49 minutes can be estimated by calculating 25% of the total number of employees:
25% of 27 employees
= (25/100) x 27
= 6.75
Since we cannot have a fractional number of employees, we round up to the nearest whole number.
Therefore,
Approximately 7 employees took a break longer than 49 minutes.
Learn more about the interquartile range here:
https://brainly.com/question/29204101
#SPJ1

Enter the correct answer in the box.
Write the expression (x4)8 in simplest form.

Answers
Answer:
x³²
Step-by-step explanation:
When raising exponents to another power, multiply the exponents given.
That means that:
(x⁴)⁸ = x⁽⁴⁾⁽⁸⁾ = x³²
Suppose a random sample of size 50 is selected from a population with μ = 10. Find the value of the standard error of the mean in each of the following cases (use the finite population correction factor if appropriate). Round your answers to two decimal places.
a. The population size is infinite.
b. The population size is N = 50,000.
c. The population size is N = 5000.
d. The population size is N = 500.
Answers
In the question, it's σ = 10 and not μ = 10.
Answer:
A) σ_x = 1.4142
B) σ_x = 1.4135
C) σ_x = 1.4073
D) σ_x = 1.343
Step-by-step explanation:
We are given;
n = 50
σ = 10
A) Formula for standard error of the mean for infinite size is;
σ_x = σ/√n
Thus;
σ_x = 10/√50
σ_x = 1.4142
B) When population is finite, we use correction factor and thus, we have;
σ_x = [√((N - n)/(N - 1)] × σ/√n
N = 50,000
Thus;
σ_x = [√((50000 - 50)/(50000 - 1)] × 10/√50
σ_x = 1.4135
C) N = 5000
Thus;
σ_x = [√((5000 - 50)/(5000 - 1)] × 10/√50
σ_x = 1.4073
D) N = 500
Thus;
σ_x = [√((500 - 50)/(500 - 1)] × 10/√50
σ_x = 1.343
If the area of a square inscribed in a circle is
25, what is the area of the circle?
Answers
The area of a square inscribed in a circle is 25, then the area of the circle is 25π/2 or approximately 39.27 square units.
To solve this problem, we can use the relationship between the area of a square inscribed in a circle and the area of the circle itself.
When a square is inscribed in a circle, the diagonal of the square is equal to the diameter of the circle. Let's assume that the side length of the square is 's' and the radius of the circle is 'r'.
We are given that the area of the square is 25, so we can find the side length of the square:
Area of square = \(s^2 = 25\)
Taking the square root of both sides, we get:
s = √25 = 5
Since the diagonal of the square is equal to the diameter of the circle, we can find the diameter of the circle:
Diagonal = Diameter = s√2 = 5√2
The radius of the circle is half the diameter, so:
Radius = 5√2 / 2 = (5√2)/2
Now, we can calculate the area of the circle using the formula:
Area of circle = \(\pi r^2\)
Substituting the value of the radius, we get:
Area of circle = π((5√2)/\(2)^2\) = π(25/2) = 25π/2
Therefore, the area of the circle is 25π/2 or approximately 39.27 square units.
For more question on square visit:
https://brainly.com/question/428672
#SPJ8