14 bags of candy for 36.26
Answers
Related Questions
Triangle KLM repreent a ection of a park et aide for picnic table. The picnic area will take up approximately 400 quare yard in the park. Triangle K L M i hown. The length of K M i 45 yard and the length of L M i 20 yard. Angle L K M i 25 degree. Trigonometric area formula: Area = One-half a b ine (C)
To the nearet yard, what amount of fencing i needed to urround the perimeter of the picnic area?
95 yard
107 yard
160 yard
190 yard
Answers
The amount of fencing needed to surround the perimeter of the picnic area of the park is 107 yards. Hence, the second option is the right choice.
In the question, we are informed that the triangle KLM, represents a section of a park set aside for picnic tables. We are also informed that the picnic area will take up approximately 400 square yards of the park.
We are asked for the amount of fencing needed to surround the perimeter of the picnic area of the park.
We know the area of a triangle can be found using the trigonometric area formula, Area = (1/2)ab sin C.
Using this in the given triangle KLM, we get:
Area = (1/2)(KL)(KM)(sin K),
or, 400 = (1/2)(KL)(45)(sin 25°),
or, KL = (400*2)/(45*sin 25°) = 800/(45*0.42262) = 800/19.017822 = 42.0658 ≈ 42 yd.
Thus, we get KL = 42 yards.
Now, the perimeter of the picnic area = the perimeter of the triangle KLM = KL + LM + MK = 42 + 20 + 45 yards = 107 yards.
Thus, the amount of fencing needed to surround the perimeter of the picnic area of the park is 107 yards. Hence, the second option is the right choice.
Learn more about the perimeter of a triangle at
brainly.com/question/3757003
#SPJ4
Answer: b
Step-by-step explanation:
what is the probability that a positive integer not exceeding 100 selected at random is divisible by 5 or 7
Answers
Answer:
So, the probability of selecting a number from 1 to 100 that is divisible by 5 or 7 is 0.32.
Hope this helped!
(d) What is the probability that the actual weight is within 0.2 g of the prescribed weight? (Round your answer to four decimal places.)
(e) What is the probability that the actual weight differs from the prescribed weight by more than 0.3 g? (Round your answer to four decimal places.)
Answers
The probability that the actual weight is within 0.2 g of the prescribed weight is 0.6827 (rounded to four decimal places)
To answer these questions, we need to use the concept of normal distribution. Let's assume that the weights of the pills follow a normal distribution with mean μ = 2 g and standard deviation σ = 0.1 g.
(d) To find the probability that the actual weight is within 0.2 g of the prescribed weight, we need to find the area under the normal curve between the values of 1.8 g and 2.2 g (i.e., within 0.2 g of the mean). We can use a standard normal distribution table or a calculator to find this probability.
Using a calculator, we can use the normalcdf function with the following inputs: normalcdf(1.8, 2.2, 2, 0.1). This gives us a probability of 0.6827. Therefore, the probability that the actual weight is within 0.2 g of the prescribed weight is 0.6827 (rounded to four decimal places).
(e) To find the probability that the actual weight differs from the prescribed weight by more than 0.3 g, we need to find the area under the normal curve outside the values of 1.7 g and 2.3 g (i.e., more than 0.3 g away from the mean). We can use a standard normal distribution table or a calculator to find this probability.
Using a calculator, we can find the probability of being below 1.7 g and above 2.3 g separately and then add them together. For example, we can use the normalcdf function with the following inputs: normalcdf(-1000, 1.7, 2, 0.1) + normalcdf(2.3, 1000, 2, 0.1). This gives us a probability of 0.0228. Therefore, the probability that the actual weight differs from the prescribed weight by more than 0.3 g is 0.0228 (rounded to four decimal places).
Learn more about probability here:
https://brainly.com/question/30034780
#SPJ11
Answer question BA survey approximates the number of Americans that are age 65 and older and projects that by the year 2050, approximately 82.4 million Americans will be at least65. The bar graph shows the estimated number of Americans with projected figures for the year 2020 and beyond.A graphing calculator screen displays an exponential function that models the U.S. population age 65 and over, y, in millions,x years after 1899. Use this information to solve (a)-(d) below.ExpRegy = ab'xClick the icon to view the bar grapha = 3.4781166081b= 1.023023196a. Explain why an exponential function was used to model the population data.OA. An exponential function was used because population is always modeled using exponential functions.B. An exponential function was used because exponential functions are always more accurate than linear functions.C. An exponential function was used because there are too many data points to use a linear function.D. An exponential function was used because the data in the bar graph is increasing more and more rapidly.b. Use the graphing calculator screen to express the model in function notation, with numbers rounded to three decimal places.
Answers
Solution
- The formula for the exponential function is:
\(y=ab^x\)- Thus, the function required is
\(\begin{gathered} a=3.4781166...\approx3.478\text{ \lparen To 3 dp\rparen} \\ b=1.0230231...\approx1.023\text{ \lparen To 3dp} \\ \\ \\ y=3.478(1.023)^x \end{gathered}\)Which is ⁴√81x³y⁴z8 with rational exponents?
(a) 3x(¾)yz²
(b) 8x (¾) yz²
(c) 2x (⅓) yz²
(d) 9x (⅓) yz²
Answers
The expression of ⁴√(81x³y⁴z⁸) with rational exponents is: 3x(¾)yz²
How to solve Laws of Exponents?The 8 laws of exponents can be listed as follows:
Zero Exponent Law: a^(0) = 1.
Identity Exponent Law: a^(1) = a.
Product Law: a^m × a^n = a^(m+n)
Quotient Law: a^m/a^n = a^(m - n)
Negative Exponents Law: a^(-m) = 1/a^(m)
Power of a Power: (a^m)^n = a^(mn)
Power of a Product: (ab)^m = a^m*b^m
Power of a Quotient: (a/b)^m = a^m/b^m
We are given the algebra expression as:
⁴√81x³y⁴z⁸
This gives us:
81^(1/4) * x^(3/4) * y^(4/4) * z^(8/4)
= 3x^(3/4)yz²
Read more about Laws of Exponents at: https://brainly.com/question/11761858
#SPJ1
The gasoline gauge on a truck reads 1/8 full. after you add 30 gallons the gauge reads 3/4 full. what is the capacity of the tank?
Answers
Answer:
48 gallons
Step-by-step explanation:
\( \frac{3}{4} = \frac{6}{8} \\ \frac{6}{8} - \frac{1}{8} = \frac{5}{8} \\ 5 \div 30 = 6 \\ 6 \times 8 = 48\)
Which equation shows the commutative property of addition? 4 3 = 3 4 1(3) = 3 (2 7) 12 = 2 (7 12) 4 0 = 4
Answers
The equation which shows the commutative property of addition is (A) 4+3=3+4.
What is the commutative property of addition?The commutative property is concerned with arithmetic operations such as addition and multiplication. It indicates that switching the order or position of two numbers while adding or multiplying them has no effect on the outcome. For example, 4 + 5 equals 9, and 5 + 4 equals 9.So,
The commutative property for addition states that, a + b = b + a .
Where a, b is any number.
The above condition is satisfied by the equation
4 + 3 = 3 + 47 = 7Therefore, the equation which shows the commutative property of addition is (A) 4+3=3+4.
Know more about the commutative property of addition here:
https://brainly.com/question/778086
#SPJ4
The correct question is given below:
Which equation shows the commutative property of addition?
A. 4+3=3+4
B. 1(3)=3
C. (2+7)+12=2+(7+12)
D. 4+0=4
Rewrite tan 36° in terms of its cofunction. tan 36⁰ = (Type an exact answer. Simplify your answer. Type any angle
Answers
tan 36° can be written as cot 54°, which simplifies to (√3 + 1) / (√3 - 1).
The tangent of 36° can be expressed in terms of its cofunction, which is the cotangent. The cotangent of an angle is equal to the reciprocal of the tangent of that angle. Therefore, we can rewrite tan 36° as cot (90° - 36°).
Now, cot (90° - 36°) can be simplified further. The angle 90° - 36° is equal to 54°. So, we have cot 54°.
The cotangent of 54° can be determined using the unit circle or trigonometric identities. In this case, the exact answer for cot 54° is (√3 + 1) / (√3 - 1).
Hence, tan 36° can be written as cot 54°, which simplifies to (√3 + 1) / (√3 - 1).
Learn more about trigonometric identities here:
https://brainly.com/question/24377281
#SPJ11
find f'(x) when f(x) = (x^2) - 2x. find the equation of the tangent line and the normal line at x=4
Answers
The derivate of a function f(x) is determinated as:
\(f^{\prime}(x)=\lim _{h\to0}\frac{f(x+h)-f(x)}{h}\)For the function
\(f(x)=x^2-2x\)First we have to determine de f ( x + h ) as follow:
\(f(x+h)=(x+h)^2-2(x+h)\)\(f(x+h)=x^2+2xh+h^2-2x-h^{}\)Then we calculate and simplify the coeficient in the first formula
\(\frac{f(x+h)-f(x)}{h}\)\(\frac{(x^2+2xh+h^2-2x-h^{})-(x^2-2x)}{h}\)\(\frac{x^2+2xh+h^2-2x-h^{}-x^2+2x}{h}=\frac{h^2+2xh-h}{h}\)\(\frac{h^2+2xh-h}{h}\text{ = }\frac{h(h+2x-1)}{h}=h+2x-1\)So the derivate is:\(f^{\prime}(x)=\lim _{h\to0}\frac{f(x+h)-f(x)}{h}=\lim _{h\to0}h+2x-1\)\(f^{\prime}(x)=0+2x-1\)\(f^{\prime}(x)=2x-1\)------------------------------------------------------------------------------------The equation of the tangent:
First you need to know that the derivate of a function is equal to the slope (m) of the tangent of this function
And the equation to thist tangent in a specific point will be find using the next formula:
\(y-f(x_0)=m(x-x_0)_{}\)We have to calculate the slope in the point x =4 using the derivate:
\(m=2x-1\)\(m=2(4)-1=7\)In the point x=4
Calculate the value of f(x0) substituting in the function the given point x:
\(f(4)=4^2-2(4)\text{ = }8\)Knowing that we put the value of m and f(x0) in the equation of the tangent:
\(y-8=7(x-4)_{}\)\(y-8=7x-28\)\(y=7x-28+8\)So the equation of the tangent in x= 4 is:\(y=7x-20\)---------------------------------------------------------------------------
The normal line
The slope of the normal line is the opposite of the slope of theu tangent in an espesific point:
\(m_n=-\frac{1}{m_t}\)So in this situation is:
\(m_n=-\frac{1}{7}\)The equation of the normal line is given by the next formula:
\(y-f(x_0)=m_n(x-x_0)_{}\)Replacing the data we obtain:
\(y-8=-\frac{1}{7}(x-4)_{}\)\(y-8=-\frac{1}{7}x+\frac{4}{7}\)So the equation of the normal line is:\(y=-\frac{1}{7}x+\frac{60}{7}\)In March, Isaiah and Freddie had the same amount of money in their savings accounts. In April, Isaiah deposited $210 into his account. Freddie increased the money in his account by 15%. When they compared their balances, they found that they were still equal.
Answers
x + 210 = 1.15x where x is the amount in their accounts in March....subtract x from both sides 210 = .15x divide both sides by .15 x = $ 1400 Hope you get an A+ :))
Good morning/Evening, i hope ur having a great day can you please solve this by today?
PROBLEM SOLVING m angle U = 2x degree, and m angle V = 4m angle U.
Which value of x makes angle U and angle V complements of
each other?
A. 25
B. 9
C. 36
D. 18
the image of the question is attached

Answers
Answer:
B. 9
Step-by-step explanation:
m∠U = 2x°
m∠V = 4m∠U
= 4(2x°)
= 8x°
Complementary angles add up to 90°.
∠U + ∠V = 90°
2x° + 8x° = 90°
10x° = 90°
x = 90° ÷ 10°
= 9
A tree is currently 10 feet tall and grows 2 feet per year. Show your work for full credit.
a. Model this scenario with an arithmetic sequence in explicit form. (2)
b. Rewrite the explicit form of the sequence using function notation. (2)
c. How tall will the tree be in 15 years? (1)
Answers
Answer:
(a) An = 2n +8
(b) F(n) = 10 + (n-1)2
(c) 38ft tall
Step-by-step explanation:
The tree is currently 10 feet long and grown 2 feet per year.
The arithmetic sequence is
10 , 12, 14 , 16 , 18 ..............
a( initial value) = 10 , d (common difference) = 2
Explicit forms
(a) An = a +(n-1)d
An = 10 + (n-1)2
= 10 + 2n -2
An = 2n +8
(b) F(n) = 10 + (n-1)2
(c) Height of the tree after 15 years
F(15) = 10 + (15-1)2
= 10 + 28
= 38ft
So the tree will be 38ft tall after 15 years.
find the power series solution to x^2y''-x(1 x)y' y=0 at x=0 with generalformula for the coefficients
Answers
The power series solution to x²y'' - x(1 + x)y' + y = 0 at x = 0 with the general formula for the coefficients.
The differential equation is x²y'' - x(1 + x)y' + y = 0.
To find the power series solution for this differential equation at x = 0, we assume a power series solution of the form y = ∑anxⁿ.
We substitute this power series in the differential equation and we get:
(x²y'' - x(1 + x)y' + y) = 0
x²(∑anⁿ(n - 1)xⁿ⁻²) - x(1 + x)(∑anⁿxⁿ⁻¹) + (∑anxⁿ) = 0.
We use the product rule of differentiation to get:
(x²∑anⁿ(n - 1)xⁿ⁻²) - (x²∑anⁿ(n - 1)xⁿ⁻² + x∑anⁿxⁿ⁻¹) + (∑anxⁿ) = 0.
This can be simplified as:
(∑anⁿ(n - 1)xⁿ) - (∑anⁿ(n + 1)xⁿ) + (∑anxⁿ) = 0.(∑anⁿ(n - 1)xⁿ) - (∑anⁿ(n + 1)xⁿ) + (∑anxⁿ) = 0.
This equation holds true for all x. For simplicity, we can set the coefficients of xⁿ to zero.
Then, we have the following relations for the coefficients:For n = 0, an + a1 = 0.
For n > 1, an = (n + 1)aₙ₋₁ / (n - 1) - aₙ₋₂.The general formula for the coefficients is given by:an = (n + 1)aₙ₋₁ / (n - 1) - aₙ₋₂.
We can use the initial conditions to determine the values of a0 and a1.
We can also use the recurrence relation to calculate the other coefficients.
Thus, we can obtain the power series solution to x²y'' - x(1 + x)y' + y = 0 at x = 0 with the general formula for the coefficients.
Know more about the power series solution
https://brainly.com/question/14300219
#SPJ11
A recipe uses 5 cups of water for
every 3 cups of flour?
Answers
Answer:
There's no context for a conclusion.
Step-by-step explanation:
Comment when you've edited the question.
Carlos took a total of 8 quizzes over the course of 4
weeks. After attending 7 weeks of school this
quarter, how many quizzes will Pancho have taken in
total?
Help,no links
Answers
Answer:
the answer is 14
Step-by-step
multiply 2x7
Laura has a collection of coins that includes pennies, nickels, dimes, and quarters. The total amount of money she has in dollars can be found using the expression (P + 5N + 10D + 25Q) ÷ 100
Answers
Answer:
3.84
Step-by-step explanation:
((24) + 5(12) + 10(10) + 25(8)) ÷ 100 = (24 + 60 + 100 + 200) ÷ 100 Multiply.
= (384) ÷ 100 Add.
= 3.84 Divide.
A card is drawn from a normal 52 card deck. The card number and sum are noted, the card is placed back in the deck, then another card is drawn. Find the probability that a) the first card was a queen and the second card as a 10. b) the first card was the Queen of Hearts and the second card was an 8. c) both cards were Jacks. d) the first card was the 5 of Spades and the second card was the Ace of Hearts.
Answers
Step-by-step explanation:
a) There are 4 Queens in a deck, so the probability the first card is a Queen is 4/52 = 1/13.
There are 4 10s in a deck, so the probability the second card is a 10 is 4/52 = 1/13.
The probability of both events is 1/13 × 1/13 = 1/169.
b) There is 1 Queen of Hearts in a deck, so the probability the first card is a Queen of Hearts is 1/52.
There are 4 8s in a deck, so the probability the second card is a 8 is 4/52 = 1/13.
The probability of both events is 1/52 × 1/13 = 1/676.
c) There are 4 Jacks in a deck, so the probability the first card is a Jack is 4/52 = 1/13.
There are 4 Jacks in a deck, so the probability the second card is a Jack is 4/52 = 1/13.
The probability of both events is 1/13 × 1/13 = 1/169.
d) There is 1 5 of Spades in a deck, so the probability the first card is a 5 of Spades is 1/52.
There is 1 Ace of Hearts in a deck, so the probability the first card is a Ace of Hearts is 1/52.
The probability of both events is 1/52 × 1/52 = 1/2704.
Find the Taylor series for F(x) centered at the given value of a. [Assume that f has a power series expansion. Do not show that Rn(x)→0. f(x)=x^4 - 4x^2 + 3, a = 2
[infinity]
a. Σ f^n(2)/n! (x-2)^n = -3 -16(x-2) + 20(x-2)^2 + n=0 8(x-2)^3 + (x-2)^4
[infinity]
b. Σ f^n(2)/n! (x-2)^n = -3 +16(x-2) + 20(x-2)^2 + n=0 8(x-2)^3 + (x-2)^4
[infinity]
c. Σ f^n(2)/n! (x-2)^n = 3 +16(x-2) + 8(x-2)^2 + n=0 20(x-2)^3 + (x-2)^4
[infinity]
d. Σ f^n(2)/n! (x-2)^n = 3 +16(x-2) - 8(x-2)^2 + n=0 20(x-2)^3 - (x-2)^4
[infinity]
e. Σ f^n(2)/n! (x-2)^n = 3 +16(x-2) + 20(x-2)^2 + n=0 8(x-2)^3 + (x-2)^4
Find the associated radius of convergence R.
R = ____
Use a Maclaurin series in this table to obtain the Maclaurin series for the given function. f(x) = 2x cos(1/3x^2) Evaluate the indefinite integral as an infinite series.
∫ cos x -1/x . dx
[infinity]
Σ + C
n=1
Answers
The correct answer is:
\(b. \sum f^n(2)/n! (x-2)^n = -3 +16(x-2) + 20(x-2)^2 + \sum 8(x-2)^3^/^n! + \sum (x-2)^4^/^n!\)
The Maclaurin series is:
\(f(x) = \sum (-1)^n (2x)^(^4^n^+^1^)/(3^(^2^n^)^(^2^n^)!) = \sum (-1)^n (2^(^4^n^+^1^)/3^(^2^n^)^(^2^n^)!) x^(^4^n^+^1^)\)
The indefinite integral of (cos(x) - 1/x) can be expressed as an infinite series.
Which statement about Taylor series for F(x) is true?The correct answer for the Taylor series of f(x) = x^4 - 4x^2 + 3 centered at a = 2 is:
\(b. \sum f^n(2)/n! (x-2)^n = -3 +16(x-2) + 20(x-2)^2 + \sum 8(x-2)^3^/^n! + \sum (x-2)^4^/^n!\)
The associated radius of convergence for this series is infinity, since the power series expansion of f(x) exists for all real numbers x.
How to find Maclaurin series for f(x)?To obtain the Maclaurin series for \(f(x) = 2x cos(1/3x^2)\), we can first find the Maclaurin series for \(cos(x^2^/^3^)\) and then multiply by 2x:
\(cos(x^2/3) = \sum (-1)^n (x^2/3)^(2n)/(2n)! = \sum (-1)^n x^(^4^n^)/(3^(^2^n^)^(^2^n^)!)\)
Therefore, the Maclaurin series for \(f(x) = 2x cos(1/3x^2)\) is:
\(f(x) = \sum (-1)^n (2x)^(^4^n^+^1^)/(3^(^2^n^)^(^2^n^)!) = \sum (-1)^n (2^(^4^n^+^1^)/3^(^2^n^)^(^2^n^)!) x^(^4^n^+^1^)\)
How to evaluate the indefinite integral?To evaluate the indefinite integral ∫(cos(x) - 1/x) dx as an infinite series, we can use the Maclaurin series for cos(x) and the power series expansion of \(ln(x) = \sum(-1)^(^n^+^1^) (x-1)^n/n\), which converges for 0 < x ≤ 2. Thus, we have:
\(\int(cos(x) - 1/x) dx = \intcos(x) dx - \int(1/x) dx = \sum(-1)^n x^(^2^n^+^1^)/(2n+1)! - ln|x| + C\)
where C is the constant of integration. We can simplify this expression as follows:
\(\int (cos(x) - 1/x) dx = \sum (-1)^n x^(^2^n^+^1^)/(2n+1)! - ln|x| + C\)
\(= -ln|x| + \sum(-1)^n x^(^2^n^+^1^)/(2n+1)!\)
\(= -ln|x| + \sum(-1)^n (x-1)^(^2^n^+^1^)/(2n+1)x^(^2^n^+^1^)\)
Thus, the indefinite integral of (cos(x) - 1/x) can be expressed as an infinite series.
Learn more about Taylor series
brainly.com/question/29733106
#SPJ11
what are the measures of angles 1,2,3, and 4?
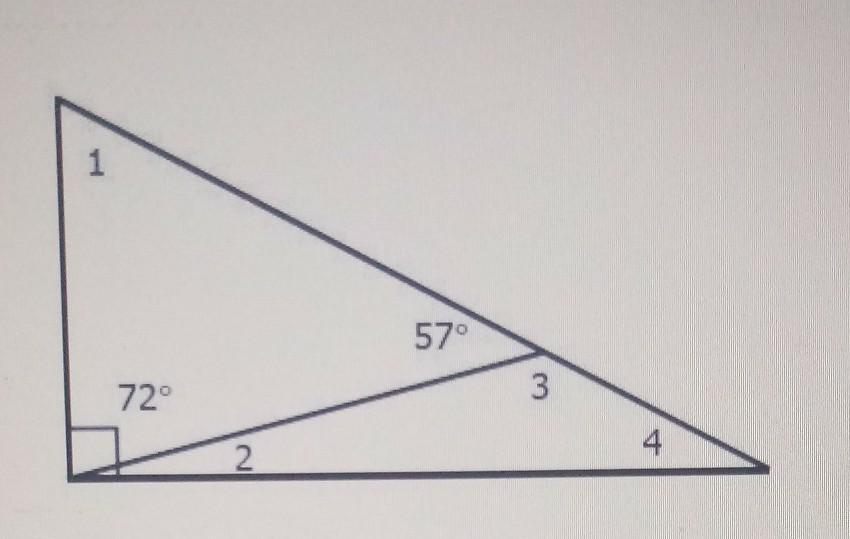
Answers
Answer:
I know that 2 is 18
The variable f varies inversely as the square root of g. When f = 4, g = 4. Jordan’s work finding the value of f when g = 100 is shown: f = k 4(4) = k 16 = k f = 16 f = 16 10f = 16 f = 1.6 What is the first error, if any, in Jordan’s work?
Answers
Variation can be direct, inverse or jointly
Jordan's first error is that he incorrectly calculated the value of proportionality constant
From the question, we understand that f varies directly as the square root of g.
This variation is represented as:
\(\mathbf{ f\ \alpha\ \frac{1}{\sqrt{g}}}\)
Express as a equation
\(\mathbf{ f\ \ =\ k\frac{1}{\sqrt{g}}}\)
When f = 4, k = 4.
So, we have:
\(\mathbf{ 4\ \ =\ k\frac{1}{\sqrt{4}}}\)
\(\mathbf{ 4\ \ =\ \frac{k}{2}}\)
Multiply both sides by 2
\(\mathbf{ k = 8}\)
When g = 100, we have:
\(\mathbf{ f\ \ =\ k\frac{1}{\sqrt{g}}}\)
\(\mathbf{ f\ \ =\ 8 \times \frac{1}{\sqrt{100}}}\)
\(\mathbf{ f\ \ =\ 8 \times \frac{1}{10}}\)
\(\mathbf{ f\ \ = 0.8}\)
This means that, Jordan incorrectly calculated the value of proportionality constant
Read more about variation at:
https://brainly.com/question/1698891
Stephen can deliver 14 newspapers in 20 minutes. How many hours will it. Take him to deliver 98 papers ?

Answers
a) To make the table for the proportional relationship, given that he delivers 14 newspapers in 20 minutes, the first step is to determine the unit rate (or constant of proportionality), that is, the number of papers he delivers in one minute.
Let x be the time in minutes and y be the number of newspapers delivered, their relationship can be expressed as:
\(y=kx\)Where k is the constant of proportionality, you can calculate it as:
\(k=\frac{y}{x}\)For x=20 and y=14
\(k=\frac{14}{20}=\frac{7}{10}=0.7\)The unit rate is 0.7 newspapers per minute.
if r is the ring of integers, let u be the ideal consisting of all multiples of 17. prove that if v is an ideal of r and r ⊃ v ⊃ u then either v = r or v = u. generalize!
Answers
(a) is a prime ideal of R, and since v is contained in (a), we have either v = (a) or v = R. Therefore, The only ideals of R containing u are u and R itself.
To prove that if v is an ideal of r and r ⊃ v ⊃ u, then either v = r or v = u, we need to use the fact that the only ideals of r are the trivial ones (0 and r) and the maximal ones (prime ideals). Since u is not a prime ideal (since it contains multiples of 17), the only possibilities for v are u and r. To see this, suppose that v is a proper ideal of r containing u. Then there exists some non-zero element a in v that is not in u. Since a is not a multiple of 17, it must have a prime factor p that is not 17 (otherwise, it would be a multiple of 17). But then (a) is a prime ideal of r (since r is a UFD), and since v is contained in (a), we have either v = (a) or v = r. Therefore, we have shown that if v is an ideal of r and r ⊃ v ⊃ u, then either v = r or v = u. We can generalize this result to any ring R and any proper ideal u of R by using the same argument. If v is a proper ideal of R containing u, then there exists some non-zero element a in v that is not in u. But then (a) is a prime ideal of R, and since v is contained in (a), we have either v = (a) or v = R. Therefore, the only ideals of R containing u are u and R itself.
Learn more about trivial ones here:
https://brainly.com/question/6848559
#SPJ11
13. Construct Argument Tommy earned $76.00 in interest after 5 years on
a principal of $400. Jane earned $82.00 in interest after 2 years on a
principal of $1,000.MP3
Which bank would you rather use, Tommy's or Jane's? Why?
Answers
The second bank is better since they've a higher interest rate.
How to calculate the interest?Tommy earned $76.00 in interest after 5 years on a principal of $400. The interest rate will be calculated thus:
Rate = 100I / PT
where I = interest
p = principal
t = time
Rate = 100I / PT
Rate = (100 × 76) / 400 × 5
Rate = 7600 / 2000
Rate = 3.8%
Jane earned $82.00 in interest after 2 years on a
principal of $1,000. The interest rate will be calculated thus:
Rate = 100I / PT
where I = interest
p = principal
t = time
Rate = 100I / PT
Rate = (100 × 82) / 1000 × 2
Rate = 8200 / 2000
Rate = 4.1%
The second bank is better.
Learn more about interest on:
brainly.com/question/25793394
#SPJ1
Object B has a mass of 10kg. Object b collides with another object. If the momentum of object b after collision is 18kg•m/s18kg.m/s, its volocity is_____m/s
Answers
Answer:
Step-by-step explanation:
Which line of best fit accurately represents the given scatter plot?

Answers
Because the best line of fit is a line that goes between the plotted points and it HAS to be a straight line and most of the points close to the line
Wingard Credit Union is redesigning the entryway into its bank of ATM machines. Management is interested in understanding how long customers spend in front of the ATMs. Customer service times follow an Exponential distribution, with an average customer taking 3.9 minutes to complete a transaction. Calculate the probability that a customer will take less than two minutes. Additionally, calculate the probability that a customer will take more than 4 minutes. The probability that a customer will take less than two minutes is \%. (Enter your response rounded to one decimal place.) a what is the probability a customer will take less than 2 mins?
b. what is the probability that a customer will take more that 4 mins ?
Answers
According to the question a.) the probability that a customer will take less than two minutes is 0.424 or 42.4%. b.) the probability that a customer will take more than four minutes is 0.097 or 9.7%.
Let's calculate the probabilities using the given information.
a. Probability that a customer will take less than 2 minutes:
The average customer service time is 3.9 minutes, which corresponds to λ (lambda) in the exponential distribution. Plugging in the values, we have:
\(P(X < 2) = 1 - e^\(-3.9 * 2\)
Calculating this expression, we find:
P(X < 2) ≈ 0.424
Therefore, the probability that a customer will take less than two minutes is approximately 0.424 or 42.4%.
b. Probability that a customer will take more than 4 minutes:
Using the same average customer service time of 3.9 minutes, we can calculate:
\(P(X > 4) = e^\(-3.9 * 4\)
Calculating this expression, we find:
P(X > 4) ≈ 0.097
Therefore, the probability that a customer will take more than four minutes is approximately 0.097 or 9.7%.
To know more about Probability visit -
brainly.com/question/15210925
#SPJ11
The water's edge restaurant is currently running an offer of 15% of all food.
Chicken curry..........£6.20
Onion soup..............£4.00
Naan Bread..............£2.80
Mint Parfait................£3.80
Ice cream Delight....£2.60
How much do Dawn and Martin spend if they buy 2 chicken curries, 2 Onion soups, 1 Nann bread, 1 Mint parfait and 1 Ice cream delight?
£_____________
(If you don't know just tell me how to find 15% pls)

Answers
4x2=8
Add 2.80 to the above 20.40
23.20
Add 3.80 =27
Finally add 2.60 so total is 29.60
10% would be 2.96 - half of this is 1.48 (5%) so 15% would be 4.44
Answer:
1 . Chicken curries - £6.20 X 2 = £12.40 15% of £ 12.40 is £1.86 off = £10.54 +
2 .Onion Soups - £4.00 x 2 = £8.00 15% OF £8.00 is £ 1.20 off = £6.80
3. One Naan bread = £.2.80 15% of £ 2.80 is £ 0.42 p off = £2.38
4. One mint parfait = £ 3.80 15% of £ 3.80 is £ 0.57 p off = £ 3.23
5 .One ice cream delight = £2.60 15% of £ 2.60 is £0.39 p off £ 2.21
= £ 25.16
Step-by-step explanation:
1. to find out 15% from £12.40 you can divide 12.40 / 100 = 0.124 and then times 0.124 by the percentage = 0.124 x 15 = £ 1.86
2 . to find out 15% from £8.00 you divide again £8.00 / 100 =0.08 and then times 0.08 by the percentage 15 %= 0.08 x 15 = £1.20 off
3. £ 2.80 / 100 =0.028 x 15% = £0.42 p off
4. £ 3.80 /100 = 0.038 x 15% = £ 0.57 p off
5. £ 2.60 /100 = 0.026 x 15% = £ 0.39 p off
Hope that helped !
At the local farmer’s market it costs $6.00 for a 4-pound basket of pears. What is the price per pound?
Answers
Answer:
$1.50 per pound
Step-by-step explanation:
You divide 6 by 4 to get 1.5
The first one-mile speed record was made by Henry Ford in 1904 when he drove the mile in 39.40 s (sec onds). This time was 33.62 s slower than the record achieved in 1970. What was the record time in 1970?
Answers
Answer:
The record time that was achieved in 1970 was 5.78 seconds.
Step-by-step explanation:
It is given that the first one-mile speed record was made by Henry Ford in 1904 when he drove the mile in 39.40 seconds.
It is further stated that this time was 33.62 s slower than the record achieved in 1970.
Now, let us consider the first statement;
Henry Ford covered one mile in time (1904) = 39.40 sec
Now, let us consider the second statement given;
Time taken by Henry Ford (1940) was slower than the time someone else achieved in one miles by = 33.62 sec
So, to calculate the time taken in 1970;
=> 39.40 - 33.62 sec
=> 5.78 sec
Therefore, the record time that was achieved in 1970 was 5.78 seconds.
To know more about this topic, click here:
https://brainly.com/question/15100186
#SPJ9
Which transformation is a translation?

Answers
Answer:
i don't know but o o o o right e o right e auto park
Answer:
4234324tgfgdfgdgd
Step-by-step explanation: