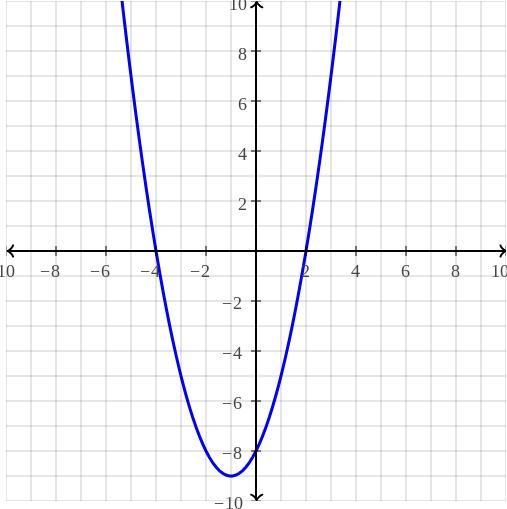
1. Sketch a graph of f(x) = (x - 2)(x + 4). Find the y-intercept, x-intercept(s), and the vertex of the graph.
Answers
Answer:
y=x2+2x−8
this is all I got sorry
Related Questions
for a standard normal distribution, find: p(-1.62 < z < 2.01)
Answers
The probability of the interval -1.62 < z < 2.01 in a standard normal distribution is approximately 0.9262 or 92.62%.
In a standard normal distribution, the mean is 0 and the standard deviation is 1. The z-score represents the number of standard deviations a data point is from the mean. To find the probability of a specific interval, we calculate the area under the curve between the corresponding z-values.
Given the interval -1.62 < z < 2.01, we need to find the area under the standard normal curve between these two z-values. This can be done using a standard normal distribution table or by using a statistical software or calculator.
By looking up the z-values in the table or using software, we find the corresponding probabilities: P(z < -1.62) = 0.0526 and P(z < 2.01) = 0.9788.
To find the probability of the interval -1.62 < z < 2.01, we subtract the probability of the lower bound from the probability of the upper bound: P(-1.62 < z < 2.01) = P(z < 2.01) - P(z < -1.62 = 0.9788 - 0.0526 = 0.9262.
Learn more about normal distribution here:
https://brainly.com/question/15103234
#SPJ11
Make u the subject of formula in
M=m(v-u).u
Answers
Answer:
u = v - 1
Step-by-step explanation:
I'm guessing the formula you've given me is m = m(v - u), and I'm going to solve it that way. If it's actually different, let me know so I can redo the answer! :)
So, we have the equation m = m(v - u) and we're trying to make u the subject, or isolate it on one side of the equation. Right now, it's being subtracted from v and then multiplied by m. Let's start by dividing both sides of the equation by m so we can stop multiplying (v - u) by m.
m = m(v - u)
m/m = m(v-u)/m
1 = v - u
Now, our equation is pretty simple, but our u is still being subtracted from v, so we should add a u to both sides.
1 = v - u
1 + u = v - u + u
1 + u = v
Now, we're adding 1 to u, so let's go ahead and subtract 1 from both sides.
1 + u = v
1 - 1 + u = v - 1
u = v - 1
And we now we have u as the subject of our formula.
Hopefully that was helpful! :)
I’m not sure I need help

Answers
Answer:
D) \(1 < x\leq 4\)
Step-by-step explanation:
1 is not included, but 4 is included, so we can say \(1 < x\leq 4\)
Write an explicit formula for each sequence and find the 7th term for each
1. -4, 12, -36
2. 12, 3, 3/4
Answers
Answer:
a[n] = -4·(-3)^(n-1); -2916a[n] = 12·(1/4)^(n -1); 3/1024Step-by-step explanation:
You want the explicit formula for each of the geometric sequences, and the 7th term.
-4, 12, -36 12, 3, 3/4Explicit formulaThe explicit formula for a geometric sequence with first term a[1] and common ratio r is ...
a[n] = a[1]·r^(n-1)
1. a[1] = -4, r = -3The explicit formula is ...
a[n] = -4·(-3)^(n-1)
The 7th term is ...
a[7] = -4·(-3)^(7-1) = -2916
2. a[1] = 12, r = 1/4The explicit formula is ...
a[n] = 12·(1/4)^(n -1)
The 7th term is ...
a[7] = 12·(1/4)^(7-1) = 3/1024
Write an equation for the parabola with the given vertex and focus.
vertex (2,4) ; focus (1,4)
Answers
The equation of the parabola, with vertex at (2 , 4) and focus (1 , 4) is y² + 4x - 8y + 8 = 0.
We use the basic definitions and terms related to a parabola on an x-y plane, to write the equation of the parabola.
Vertex is known as the epicenter of the parabola, where the curve attains a peak, minimum or maximum.
Focus is a representation of the shape of the parabola and is equidistant from the vertex as is the directrix.
Directrix is a line perpendicular to the axis of the parabola, as mentioned earlier, equidistant from the vertex.
(A diagram with representation has been given below)
Now, moving to the question,
Vertex = (2,4)
Focus = (1,4)
The slope of the line passing through them, the axis is:
m = (y₂ - y₁)/(x₂ - x₁)
m = (4 - 4)/(2 - 1)
m = 0
Which means the axis is parallel to the x-axis.
For a parabola with an axis parallel to the x-axis, vertex at (h , k), and focus lying to the left of the vertex,
(y - k)² = -4*a*(x - h)
where a is the distance between the focus and the vertex.
Here,
a = √[(2 - 1)² + 0²] (From distance formula)
a = 1
(h , k) = (2 , 4)
Thus,
(y - 4)² = -4*1*(x - 2)
y² + 16 - 8y = -4x + 8 (Expansion)
y² + 4x - 8y + 8 = 0
So, the final equation of the parabola is y² + 4x - 8y + 8 = 0.
For more on Parabolas,
brainly.com/question/9518316
#SPJ4

solve pls brainliest

Answers
Answer:
The answer is:
\( \frac{10}{3} \)
Step-by-step explanation:
Before multiplying you can turn the mixed fraction into an improper one hence:
\(4 \frac{2}{3} = \\ (3 \times 4) + 2 = \frac{14}{3} \\ \)
Now we multiply:
\( \frac{5}{7} \times \frac{14}{3} = \frac{10}{3} or \: 3 \frac{1}{3} \)
Answer:
\(\Large\boxed{\sf{3\dfrac{1}{3}}}\)Step-by-step explanation:
The solution is to convert mixed numbers into improper fractions.
5/7*4 2/3
4 2/3=4*3+2/3
4*3+2
Use the order of operations.
PEMDAS stands for:
ParenthesesExponentsMultiplyDivideAddSubtractFirst, do multiply.
4*3=12
12+2
Then, you add.
12+2=14
= 14/3
5/7*14/3
\(\Longrightarrow: \sf{\dfrac{5\cdot \:14}{7\cdot \:3}}\)
7*2=14
\(\Longrightarrow: \sf{\dfrac{5*7* \:2}{7* 3}}\)
Common factor of 7.
\(\Longrightarrow: \sf{\dfrac{5*2}{3}}\)
Multiply.
5*2=10
10/3
10/3=3 1/3
\(\Longrightarrow: \boxed{\sf{3\dfrac{1}{3} }}\)
Therefore, the final answer is 3 1/3.I hope this helps. Let me know if you have any questions.
A ship headed due east is moving through the water at a constant speed of 8 miles per hour. However, the true course of the ship is 60°. If the currents are a constant 4 miles per hour, what is the ground speed of the ship? (Round your answer to the nearest whole number. )
Answers
The ground speed of the ship is approximately 10 miles per hour.
To calculate the ground speed, we need to use vector addition. The ship's velocity can be broken down into two components: its speed in the easterly direction and its speed in the northerly direction. The easterly component is 8 miles per hour (since the ship is moving due east), and the northerly component can be found using trigonometry: northerly component = 8 * sin(60°) ≈ 6.93 miles per hour
Now, we need to take into account the effect of the currents, which are moving in a southerly direction. Again using vector addition, we can find the resultant velocity (i.e., the velocity of the ship relative to the ground) by adding the ship's velocity vector to the current's velocity vector. Since the current is moving due south, its velocity vector has no easterly component, but its southerly component is 4 miles per hour. resultant velocity = (8, 6.93) + (0, -4) = (8, 2.93)
Using the Pythagorean theorem, we can find the magnitude of the resultant velocity: |resultant velocity| = \(\sqrt{} (8^2 + 2.93^2)\)≈ 8.6 miles per hour. Rounding to the nearest whole number, the ground speed of the ship is approximately 10 miles per hour.
Learn more about Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ4
are utilized to make inferences about certain population parameters; a. samplesb. equationsc. statisticsd. metrics
Answers
The term utilized to make inferences about certain population parameters is a) samples.
In statistical analysis, samples are a subset of a larger population that are selected for observation and analysis. By studying the sample, statisticians can make inferences about the larger population from which it was drawn. This allows for predictions to be made about the entire population, based on information gathered from a smaller subset.
Equations and metrics are important in statistical analysis, but they are not used to make inferences about population parameters. Equations are used to model relationships between variables and to test hypotheses, while metrics are used to quantify the properties of data sets.
Statistics, on the other hand, is the branch of mathematics that deals with the collection, analysis, interpretation, presentation, and organization of data. Statistics is used to make sense of data and to draw conclusions about the larger population from which the sample was drawn.
In summary, samples are an important tool for statisticians to make inferences about certain population parameters, and statistics is the field that studies these methods of data analysis.
Therefore, the correct answer is a) samples.
Learn more about data analysis here: https://brainly.com/question/30156066
#SPJ11
Solve each. Show all necessary work.
8. Write the equation of the line in slope-intercept form that passes through (10.21) and (15.36)
Answers
Answer:
y = 3x - 9
Step-by-step explanation:
First, find the slope using y2 - y1 / x2 - x1
36 - 21 = 15
15 - 10 = 5
15/5 = 3, so the slope (m) is 3.
Now, plug into point-slope form: y - y1 = m (x - x1)
y - 21 = 3 (x - 10)
Simplify
y - 21 = 3x - 30
y = 3x - 9
I hope this helps!!
10 minutes left unit test PLEASE HELPP

Answers
Answer:
8/15
Step-by-step explanation:
8/15
hope this helped!!
7. Which of the following statements is not
true?
a. The square root of 112 is between 10 & 11.
b. The square root of 180 is between 13 & 14.
The square root of 12 is between 4 & 5.
d. The square root of 5 is between 2 & 3.
Answers
Answer:
c
Step-by-step explanation:
it is because in (a) the square root of 112. is 10.58 which is in between 10 and 11
(B) the square root of 180 is 13.42 which is between 13&14
(c) the square root of 12 is 3.46 which is not between 4&5
Answer:
C the square root of 12 is between 4&5.
Step-by-step explanation:
How many different numbers can be obtained using five binary bits? A)64 B)32 C)31 D)63.
Answers
In binary representation, each bit can be either 0 or 1. Using five binary bits, we can obtain 32 different numbers. Therefore, the correct answer is (B).
With five binary bits, we have five positions, and each position can have two possibilities (0 or 1). To calculate the total number of different numbers we can obtain, we need to raise 2 to the power of the number of bits. In this case, we have \(2^5,\) which equals 32. Therefore, we can obtain 32 different numbers using five binary bits. To understand this concept, we can think of each binary bit as a switch that can be either on (1) or off (0). With five switches, we have a total of 32 different combinations or numbers that can be represented. These numbers range from 0 (all switches off) to 31 (all switches on). Therefore, the correct answer is (B), which states that we can obtain 32 different numbers using five binary bits.
Learn more about binary bits here:
https://brainly.com/question/30462196
#SPJ11
Explain it too and is it x method?

Answers
So Iam not sure either what the correct answer is but that’s what I got
A nonregular hexagon has five exterior angle measures of 55, 60, 69, 57, and 57. What is the measure of the interior angle adjacent to the sixth exterior angle?
62
128
118
108
Answers
The measure of the interior angle adjacent to the sixth exterior angle of the heaxagon is 118°.
What is an interior angle?Interior angles are those that lie inside a polygon.
To calculate an interior angle of a hexagon, we use the formula below.
Formula:
a = 360-(b+c+d+e+f)............ Equation 1Where:
a = The sixth exterior angleb = 55°c = 60°d = 69°e = 57°f = 57°Substitute these values into equation 1
a = 360-(55+60+69+57+57)a = 360-298a = 62°Recall that, the sum of an interior and exterior angle is 180°
a'+a = 180............... Equation 2Where:
a = Interior angle of the sixth exterior angle.Substitute the value of a into equation 2
a' = 180-62a' = 118°Hence, the value of the interior angle is 118°.
Learn more about interior angle here: https://brainly.com/question/24966296
#SPJ1
2x.tg60= 10+csc30 plis
Answers
Answer:
\(2\sqrt{3}\)
Step-by-step explanation:
I'm assuming the angles are in degrees.
\(2x \tan(60\º)=10+\csc(30\º)\)
\($2x\cdot \sqrt{3}=10+\frac{1}{\sin(30\º)} $\)
\($2x\cdot \sqrt{3}=10+\frac{1}{\frac{1}{2} } $\)
\($2x\cdot \sqrt{3}=10+2} $\)
\($x=\frac{12}{2\sqrt{3}} $\)
\($x=\frac{6}{\sqrt{3}} =\frac{6\sqrt{3}} {3} }=2\sqrt{3} $\)
which expression below evaluates to true if and only if the units digit (also known as the one's digit or one's place) of an integer variable x is less than 8? assume x stores a non-negative integer.
Answers
The expression that evaluates to true if and only if the units digit of an integer variable x is less than 8 is :x % 10 < 8 where % is the modulo operator that gives the remainder of x divided by 10. This expression works by extracting the units digit of x using the modulo operator and then checking if it is less than 8. If it is, the expression evaluates to true.
To evaluate the truth value of an expression, we need to first understand the conditions under which it would be true and the conditions under which it would be false. The expression in question is evaluating the units digit of an integer variable x, so we need to consider the possible values that the units digit can take.Let's start by considering the values that would make the expression true. We are told that the units digit of x must be less than 8. This means that the units digit can take on any value from 0 to 7. So if the units digit of x is any of these values (0, 1, 2, 3, 4, 5, 6, or 7), then the expression would be true.Now let's consider the values that would make the expression false. The expression only evaluates to true if the units digit is less than 8, so any value of the units digit that is greater than or equal to 8 would make the expression false. This means that if the units digit of x is 8 or 9, the expression would be false.
for more search question integer
https://brainly.com/question/749791
#SPJ8
Lisa plans to make 29 savings deposits of $254 into her account one payment at the end of each month with her first savings deposit made 5 years from today. How much will she have in her account on the day she makes her final deposi?, Include the value of her last deposit in the total. Lisa can earn 4.03% per year on her deposits.
Answer Format: INCLUDE ONLY NUMBERS AND DECIMALS IN YOUR ANSWER. Do not include "$" "," or any other formatting. Carry interim computations to at least 4 decimals. Enter numerical answers as a positive number rounded to 2 decimal places
Answers
Lisa will have approximately $9,554.58 in her account on the day she makes her final deposit.
To calculate the amount Lisa will have in her account on the day she makes her final deposit, we can use the future value of an ordinary annuity formula: Future Value = Payment × [(1 + Interest Rate)^Number of Periods - 1] / Interest Rate. Given: Payment = $254 (monthly deposit); Interest Rate = 4.03% per year; Number of Periods = 29 (number of monthly deposits).
First, let's convert the annual interest rate to a monthly interest rate: Monthly Interest Rate = (1 + 0.0403)^(1/12) - 1 = 0.00332. Now, let's calculate the future value: Future Value = $254 × [(1 + 0.00332)^29 - 1] / 0.00332 ≈ $9,554.58. Therefore, Lisa will have approximately $9,554.58 in her account on the day she makes her final deposit.
To learn more about deposit click here: brainly.com/question/30346732
#SPJ11
help me ASAP PLZzzzzzz
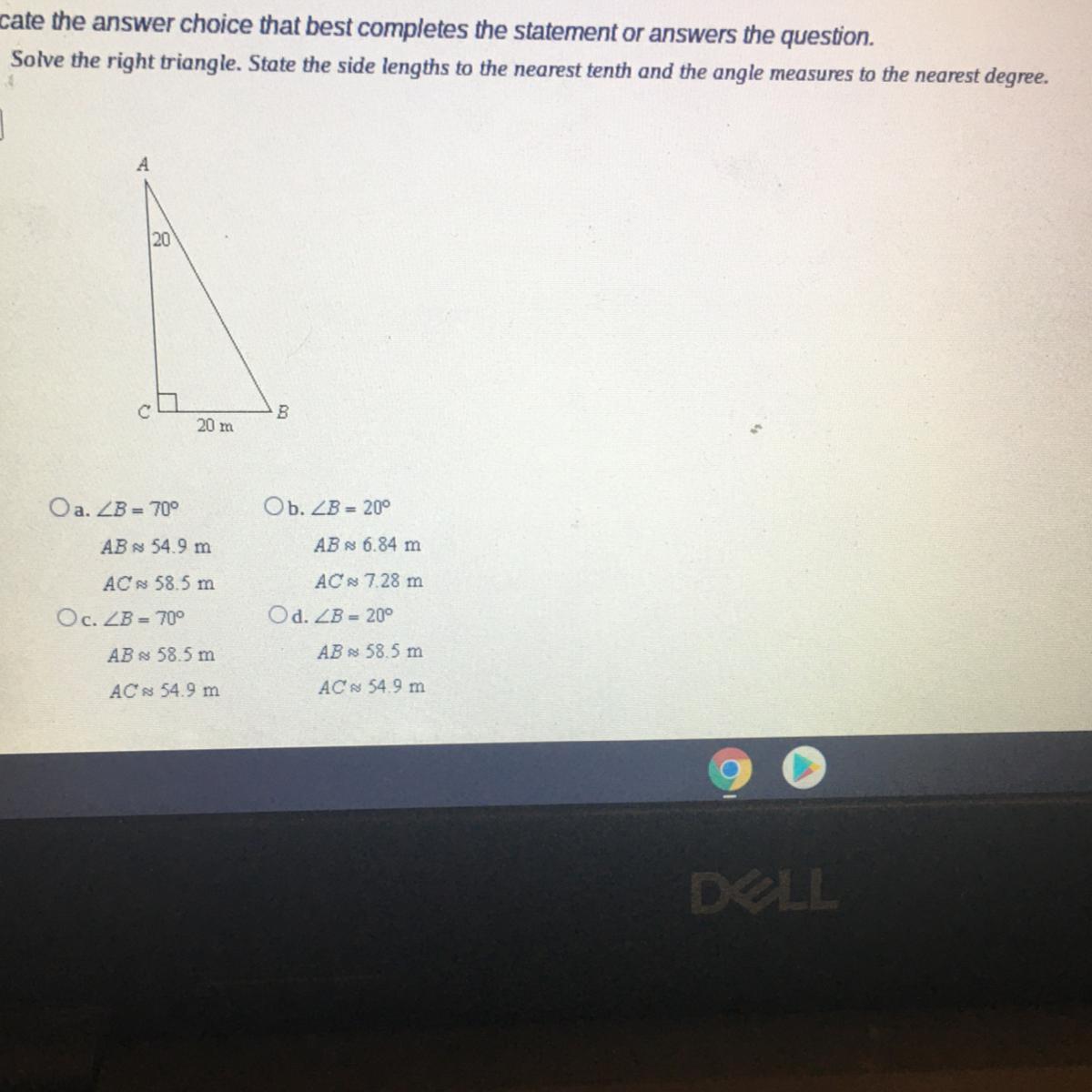
Answers
Answer:
a
Step-by-step explanation:
What is the length of the line?

Answers
Using the Pythagorean theorem, the length of the line is: √45 = 6.7 units.
How to Find the Length of a Line Using Pythagorean Theorem?The Pythagorean theorem is the equation that describes how the lengths of the three sides of a right triangle relate to each other. If a and b are smaller legs, and c us the hypotenuse of the triangle, the Pythagorean theorem states that:
c² = a² + b².
Consider the line above to be the hypotenuse of a right triangle that is formed by the rise and run of the line.
Rise = a = 3 units
Run = b = 6 units
Line = c
Therefore:
c² = 3² + 6²
c² = 9 + 36
c² = 45
c = √45
c = 6.7 units.
Learn more about Pythagorean theorem on:
https://brainly.com/question/343682
#SPJ1
The equation of line a is y=12x−1, and it passes through point (6,2).
Line b is perpendicular to line a, and it passes through point (−6,2).
A: What is the slope of line b?
B: What is the y-intercept of line b?
Answers
Answer:
A). slope = -1/12 y-intercept = 3/2
Step-by-step explanation:
y = -1/12x + b
2 = -1/12(-6) + b
2 = 1/2 + b
3/2 = b
y = -1/12x + 3/2
I need help with this
Write it as a whole number, fraction or improper faction only
Answers
Answer:
3/4
Step-by-step explanation:
I would really appreciate your help. Thank you.

Answers
Answer:
75
Step-by-step explanation:
trust me bro
luis is making a wooden model of a flag for his school project. He found a bargain on square pieces of plywood. If his flag is to be 18 inches by 12 inches,what is a reasonable area for the square piece of plywood he must purchase if he only wants to make one cut in the wood?
NEED SOON
Answers
The reasonable area for the square piece of plywood he must purchase if he only wants to make one cut in the wood would be 216 sq inches.
What is the area of the rectangle?The area of the rectangle is the product of the length and width of a given rectangle.
The area of the rectangle = length × Width
We have been given that the flag is to be 18 inches by 12 inches, then;
The area of the rectangle = length × Width
The area of the rectangle = 18 x 12
= 216
Since the area of flag will be equal to area for the square piece of plywood.
The area of a square of side length l is given by l squared;
A(l) = l²
216 = 14.6²
Hence, the reasonable area for the square piece of plywood he must purchase if he only wants to make one cut in the wood would be 216 sq inches.
Learn more about rectangles here;
https://brainly.com/question/15019502
#SPJ2
you have been an irresponsible pet owner, and failed to have your cat spayed. she's a white longhair (w/w; l/l) now, thanks to a visit from the neighbor's black shorthair tomcat (w/w; l/l), you have 12 kittens that need homes. what will the kittens look like?
Answers
Both the white longhair female cat (w/w; l/l) and the black shorthair male cat (w/w; l/l) are homozygous for the white coat color (w/w) and the longhair trait (l/l).
When these cats mate, all the kittens will inherit one allele for each trait from each parent. Since both parents are homozygous for the white coat color (w/w), all kittens will also inherit the white coat color gene from both parents, resulting in white kittens (w/w). Similarly, both parents are homozygous for the longhair trait (l/l), so all kittens will inherit the longhair allele from both parents, making them longhair kittens (l/l).
In conclusion, all 12 kittens will have a white coat color and long hair, just like their parents. They will look like white longhair kittens, with the genotype (w/w; l/l) for both traits. It is important to remember that being a responsible pet owner includes spaying or neutering your pets to prevent unwanted litters, and finding loving homes for any kittens or puppies that may be born.
For more about homozygous:
https://brainly.com/question/376455
#SPJ11
someone plz help
I HATE MATH!!!!!

Answers
Answer:
2 ft by 12 feet
Step-by-step explanation:
find the area of the region bounded by the given curves. y = 6x2 ln(x), y = 24 ln(x)
Answers
The area of the region bounded by the given curves. y = 6x2 ln(x), y = 24 ln(x) is 2.85 sq.units.
In this question we need to find the area of the region bounded by the given curves. y = 6x^2 ln(x), y = 24 ln(x)
Equating both the equations of the curve,
6x^2 ln(x) = 24 ln(x)
24 ln(x) - 6x^2 ln(x) = 0
x = 1, 2
This means, the curves intersect at x = 1 and x = 2.
So, the required area would be,
A = ∫[1 to 2] [24 ln(x) - 6x^2 ln(x)] dx
First we find the indefinite integral ∫[24 ln(x) - 6x^2 ln(x)] dx
= -6 ∫[-4 ln(x) + x^2 ln(x)] dx
= -6 ∫ln(x) (x^2 - 4) dx
= -6 ln(x) (1/3 x^3 - 4x) + 2/3 x^3 - 24x
So, ∫[1 to 2] [24 ln(x) - 6x^2 ln(x)] dx
= [-6 ln(x) (1/3 x^3 - 4x) + 2/3 x^3 - 24x] _(x = 1 to x = 2)
= 32 ln(2) - 58/3
= 22.18 - 19.33
= 2.85 sq.units.
Therefore, the area of the region is 2.85 sq.units.
Learn more about the area of the region here:
https://brainly.com/question/9485980
#SPJ4

In a certain font, a monochrome laser printer can print 50 lines of 80 characters per page. The average character occupies a box 2 mm × 2 mm, about 25% of which is toner. The rest is blank. The toner layer is 25 microns thick. The printer s toner cartridge measures 25 × 8 × 2 cm. How much toner in mm3 does it take to print a page completely full of characters?
Answers
It takes 100 mm³ of toner to print a page completely full of characters.
To calculate the amount of toner required to print a page completely full of characters, we need to determine the volume of toner used per character and then multiply it by the total number of characters on the page.
First, let's calculate the volume of toner per character. We know that the average character occupies a box 2 mm × 2 mm, and 25% of this area is toner. Therefore, the area of toner per character is:
Toner area per character = 2 mm × 2 mm × 0.25 = 1 mm²
Next, we need to calculate the volume of the toner layer for each character. We are given that the toner layer is 25 microns thick (0.025 mm). Thus, the volume of toner per character is:
Toner volume per character = Toner area per character × Toner layer thickness
= 1 mm² × 0.025 mm
= 0.025 mm³
Now, let's calculate the total number of characters on a page. We are told that the printer can print 50 lines of 80 characters per page. Therefore, the total number of characters per page is:
Total characters per page = 50 lines × 80 characters
= 4000 characters
Finally, to find the total amount of toner used to print a page completely full of characters, we multiply the volume of toner per character by the total number of characters on the page:
Total toner volume = Toner volume per character × Total characters per page
= 0.025 mm³ × 4000
= 100 mm³
Therefore, it takes 100 mm³ of toner to print a page completely full of characters.
Learn more about area here:
https://brainly.com/question/16151549
#SPJ11
Examine the diagram, where quadrilateral LMNO is inscribed in O C.
M
L
C
82
N
O
© 2016 StrongMind. Created using GeoGebra.
If mZMNO = 82°, what is mZOLM?
O 102°
O 196°
O 98°
O 124

Answers
Answer:
(c) 98°
Step-by-step explanation:
Opposite angles of an inscribed quadrilateral are supplementary.
∠OLM = 180° -∠ONM = 180° -82°
∠OLM = 98°
_____
Additional comment
The relation we used here derives from the fact that an inscribed angle is half the measure of the arc it intercepts. For two opposite angles of an inscribed quadrilateral, the sum of the arcs is 360°, so the sum of the angles will be 360°/2 = 180°.
to classify fossils of an insect, archeologists measure the length of the body. the body length of a type a insect is distributed as and the body length of a type b insect is distributed as (in millimeters). the fossil is classified as type a if the length is less than millimeters and classified as type b if the length is larger than or equal to millimeters. find the value of that the probability of correctly classifying a type a insect equals the probability of correctly classifying a type b insect (round off to first decimal place).
Answers
The value that the probability of correctly classifying a type an insect equals the probability of correctly classifying a type b insect is 4.5 millimeters.
To find the value that the probability of correctly classifying a type A insect equals the probability of correctly classifying a type B insect, we need to find the point where the probability density functions of the two types of insects intersect.
For type A insects, the probability density function is given as -
f(x) = \((1/2)e^{-{x-3}^{2/2}}\)
For type B insects, the probability density function is given as-
f(x) = \((1/4)e^{-{x-5}^{2/2}}\)
We can set these two probability density functions equal to each other and solve for x as follows -
\((1/2)e^{-{x-3}^{2/2}}\) = \((1/4)e^{-{x-5}^{2/2}}\)
Solving for x, we get:
x = 4.5
So the value that the probability of correctly classifying a type A insect equals the probability of correctly classifying a type B insect and is 4.5 millimeters. This means that if the length of the insect is 4.5 millimeters or less, it will be classified as type A, and if it is greater than 4.5 millimeters, it will be classified as type B.
Read more about Probability:
brainly.com/question/24756209
#SPJ4
Determine how large the number a has to be so that ∫[infinity]a1x2+1dx<0.001
Integrals of Inverse Trigonometric Functions
The derivative of a function f(x) is given by
ddxf(x)=g(x)
Then the integration of g(x) is given by
∫g(x)⋅dx=f(x)+C∫
We can differentiate trigonometric functions , so we can also integrate trigonometric functions.
∫1x2+1dx=tan−1x+C∫12+1=tan−1
Inverse function value of tan−1xtan−1 :
tan−1([infinity])=π2
Answers
The number a has to be greater than 636.6197723675814 for the integral ∫[infinity]a1x2+1dx to be less than 0.001.
To determine how large the number a has to be so that ∫[infinity]a1x2+1dx<0.001, we can use the formula for the integral of inverse trigonometric functions:
∫1x2+1dx=tan−1x+C
We can substitute the limits of integration into this formula:
∫[infinity]a1x2+1dx=tan−1([infinity])-tan−1(a)
Since tan−1([infinity])=π2, the formula becomes:
π2-tan−1(a)<0.001
We can rearrange this inequality to solve for a:
tan−1(a)>π2-0.001
Taking the inverse tangent of both sides of this inequality gives us:
a>tan(π2-0.001)
Using a calculator, we can find that:
a>636.6197723675814
For more similar questions on Trigonometric Functions:
brainly.com/question/25618616
#SPJ11